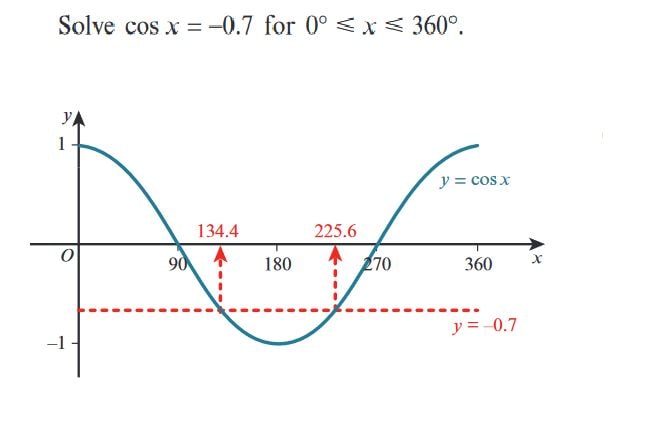
Solution \[ \text{We are solving } \cos x = -0.7 \text{ for } 0^\circ \leq x \leq 360^\circ. \] \[ \text{Step 1: Use a calculator to find the inverse cosine } \cos^{-1}(-0.7): \] \[ \cos^{-1}(-0.7) \approx 134.4^\circ \] \[ \text{One solution is } x = 134.4^\circ. \] \[ \text{Step 2: Use the symmetry of the cosine function to find the second solution.} \] \[ \text{The second solution is given by } 360^\circ - 134.4^\circ = 225.6^\circ. \] \[ \text{Step 3: The solutions to } \cos x = -0.7 \text{ are:} \] \[ x = 134.4^\circ \, \text{or} \, 225.6^\circ \] \[ \text{(Both rounded to 1 decimal place)} \]

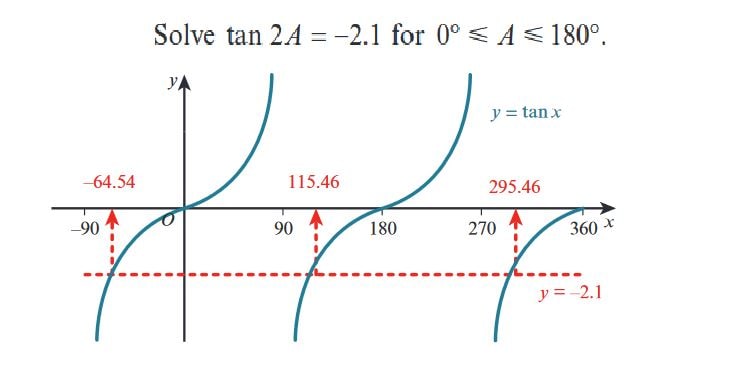
Solution \[ \text{We are solving } \tan(2A) = -2.1 \text{ for } 0^\circ \leq A \leq 180^\circ. \] \[ \text{Step 1: Find the inverse tangent of } -2.1. \] \[ \tan^{-1}(-2.1) \approx -64.54^\circ \] \[ \text{So, one solution is } 2A = -64.54^\circ. \] \[ \text{Step 2: Use the symmetry of the tangent curve to find another solution.} \] \[ 2A = -64.54^\circ + 180^\circ = 115.46^\circ \] \[ \text{Step 3: Divide by 2 to find the corresponding values of } A: \] \[ A = \frac{-64.54^\circ}{2} = -32.3^\circ \] \[ A = \frac{115.46^\circ}{2} = 57.7^\circ \] \[ \text{Step 4: Adjust the negative angle to find the second solution.} \] \[ A = 147.7^\circ \quad \text{(Adding 180 degrees to the negative angle)} \] \[ \text{Final answer: } A = 57.7^\circ \, \text{or} \, 147.7^\circ \, \text{(rounded to 1 decimal place)}. \]

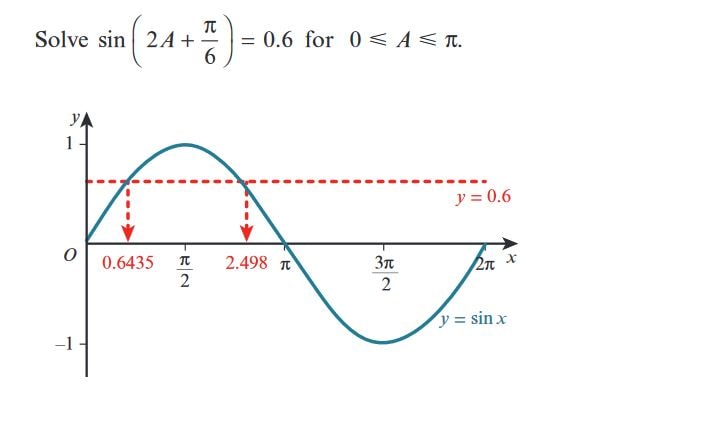
Solution \[ \text{We are solving } \sin\left(2A + \frac{\pi}{6}\right) = 0.6 \text{ for } 0 \leq A \leq \pi. \] \[ \text{Step 1: Let } x = 2A + \frac{\pi}{6}. \] \[ \text{We have } \sin x = 0.6. \] \[ \text{Step 2: Use a calculator to find } \sin^{-1}(0.6). \] \[ \sin^{-1}(0.6) \approx 0.6435 \, \text{radians}. \] \[ \text{Step 3: Use the symmetry of the sine curve to find the second solution.} \] \[ x = \pi - 0.6435 = 2.4981 \, \text{radians}. \] \[ \text{Step 4: Solve for } A. \] \[ \text{For } x = 0.6435: \] \[ 2A + \frac{\pi}{6} = 0.6435 \quad \Rightarrow \quad 2A = 0.6435 - 0.5236 = 0.1199 \quad \Rightarrow \quad A = \frac{0.1199}{2} = 0.0600 \, \text{radians}. \] \[ \text{For } x = 2.4981: \] \[ 2A + \frac{\pi}{6} = 2.4981 \quad \Rightarrow \quad 2A = 2.4981 - 0.5236 = 1.9745 \quad \Rightarrow \quad A = \frac{1.9745}{2} = 0.9873 \, \text{radians}. \] \[ \text{Final answer: } A = 0.0600 \, \text{radians} \quad \text{or} \quad A = 0.987 \, \text{radians} \quad \text{(to three significant figures)}. \]