Worked Examples
Q1
(i) Express \( x^2 + 8x + 15 \) in the form \( (x + a)^2 + b \).
Solution:
- Complete the square by adding and subtracting \( 16 \):
\[
x^2 + 8x + 15 = (x^2 + 8x + 16 - 16) + 15 = (x + 4)^2 - 1
\]
- So the expression is:
\[
(x + 4)^2 - 1
\]
Q2
(i) Express \( 2x^2 + 8x + 1 \) in the form \( a(x + b)^2 + c \).
Solution:
- Factor out the 2 from the first two terms:
\[
2x^2 + 8x + 1 = 2(x^2 + 4x) + 1
\]
- Complete the square by adding and subtracting \( 4 \) inside the bracket:
\[
2(x^2 + 4x + 4 - 4) + 1 = 2((x + 2)^2 - 4) + 1
\]
- Expand and simplify:
\[
2(x + 2)^2 - 8 + 1 = 2(x + 2)^2 - 7
\]
- So the expression is:
\[
2(x + 2)^2 - 7
\]
Q3
(i) Express \( x^2 - 6x + 4 \) in the form \( (x + a)^2 + b \).
Solution:
- Complete the square by adding and subtracting \( 9 \):
\[
x^2 - 6x + 4 = (x^2 - 6x + 9 - 9) + 4 = (x - 3)^2 - 5
\]
- So the expression is:
\[
(x - 3)^2 - 5
\]
Q4
(i) Express \( 3x^2 + 12x + 5 \) in the form \( a(x + b)^2 + c \).
Solution:
- Factor out the 3 from the first two terms:
\[
3x^2 + 12x + 5 = 3(x^2 + 4x) + 5
\]
- Complete the square by adding and subtracting \( 4 \) inside the bracket:
\[
3(x^2 + 4x + 4 - 4) + 5 = 3((x + 2)^2 - 4) + 5
\]
- Expand and simplify:
\[
3(x + 2)^2 - 12 + 5 = 3(x + 2)^2 - 7
\]
- So the expression is:
\[
3(x + 2)^2 - 7
\]
Q5
(i) Express \( x^2 + 10x + 25 \) in the form \( (x + a)^2 + b \).
Solution:
- Since \( 25 \) is already a perfect square, rewrite the expression directly:
\[
x^2 + 10x + 25 = (x + 5)^2
\]
- So the expression is:
\[
(x + 5)^2
\]
Q6
(i) Express \( x^2 - 4x + 4 \) in the form \( (x + a)^2 + b \).
Solution:
- Since \( 4 \) is already a perfect square, rewrite the expression directly:
\[
x^2 - 4x + 4 = (x - 2)^2
\]
- So the expression is:
\[
(x - 2)^2
\]
Q7
(i) Express \( 4x^2 + 16x + 9 \) in the form \( a(x + b)^2 + c \).
Solution:
- Factor out the 4 from the first two terms:
\[
4x^2 + 16x + 9 = 4(x^2 + 4x) + 9
\]
- Complete the square by adding and subtracting \( 4 \) inside the bracket:
\[
4(x^2 + 4x + 4 - 4) + 9 = 4((x + 2)^2 - 4) + 9
\]
- Expand and simplify:
\[
4(x + 2)^2 - 16 + 9 = 4(x + 2)^2 - 7
\]
- So the expression is:
\[
4(x + 2)^2 - 7
\]
Q8
(i) Express \( 5x^2 + 20x + 5 \) in the form \( a(x + b)^2 + c \).
Solution:
- Factor out the 5 from the first two terms:
\[
5x^2 + 20x + 5 = 5(x^2 + 4x) + 5
\]
- Complete the square by adding and subtracting \( 4 \) inside the bracket:
\[
5(x^2 + 4x + 4 - 4) + 5 = 5((x + 2)^2 - 4) + 5
\]
- Expand and simplify:
\[
5(x + 2)^2 - 20 + 5 = 5(x + 2)^2 - 15
\]
- So the expression is:
\[
5(x + 2)^2 - 15
\]
Q9
(i) Express \( 2x^2 + 8x + 7 \) in the form \( a(x + b)^2 + c \).
Solution:
- Factor out the 2 from the first two terms:
\[
2x^2 + 8x + 7 = 2(x^2 + 4x) + 7
\]
- Complete the square by adding and subtracting \( 4 \) inside the bracket:
\[
2(x^2 + 4x + 4 - 4) + 7 = 2((x + 2)^2 - 4) + 7
\]
- Expand and simplify:
\[
2(x + 2)^2 - 8 + 7 = 2(x + 2)^2 - 1
\]
- So the expression is:
\[
2(x + 2)^2 - 1
\]
Q10
(i) Express \( x^2 + 12x + 36 \) in the form \( (x + a)^2 + b \).
Solution:
- Since \( 36 \) is already a perfect square, rewrite the expression directly:
\[
x^2 + 12x + 36 = (x + 6)^2
\]
- So the expression is:
\[
(x + 6)^2
\]
Algebra Worksheet
Name: __________________________ Date: __________________________
Instructions:
Solve the following equations and find the real roots. Provide your final answer in the space provided.
Questions:
1) Find the real roots of the equation:
- \( \frac{9}{x^4} + \frac{8}{x^2} = 1 \)
Answer: _______________________
2) Solve:
- \( x^4 - 13x^2 + 36 = 0 \)
Answer: _______________________
3) Find the real roots of the equation:
- \( x^2 - 2 = \frac{8}{x^2} \)
Answer: _______________________
4) Solve:
Answer: _______________________
5) Solve:
- \( 2x^4 - 11x^2 + 5 = 0 \)
Answer: _______________________
6) Solve the equation:
- \( \frac{9}{x^4} + \frac{5}{x^2} = 4 \)
Answer: _______________________
7) Solve:
- \( 2x - 9\sqrt{x} + 10 = 0 \)
Answer: _______________________
8) Solve:
- \( \sqrt{x}(\sqrt{x} + 1) = 6 \)
Answer: _______________________
9) Find the x-coordinates of points A and B where the curve \( y = 2\sqrt{x} \) and the line \( 3y = x + 8 \) intersect.
Answer: _______________________
10) Find the values of \( a \), \( b \), and \( c \) for the quadratic equation \( y = ax^2 + bx + c \), given that the graph crosses the x-axis at \( (1, 0) \) and \( \left(\frac{49}{4}, 0\right) \) and meets the y-axis at \( (0, 7) \).
Answer: \( a = __________, b = __________, c = __________ \)
Answer Key:
- 1) \( x = 3 \) or \( x = -3 \)
- 2) \( x = \pm 3 \) or \( x = \pm 2 \)
- 3) \( x = 2 \) or \( x = -2 \)
- 4) \( x = 2 \) or \( x = -1 \)
- 5) \( x = \pm \sqrt{5} \) or \( x = \pm \frac{\sqrt{2}}{2} \)
- 6) \( x = \frac{3}{2} \) or \( x = -\frac{3}{2} \)
- 7) \( x = 6.25 \) or \( x = 4 \)
- 8) \( x = 4 \)
- 9) \( x = 16 \) and \( x = 4 \)
- 10) \( a = \frac{4}{7}, b = -\frac{53}{7}, c = 7 \)
Solving Difficult Quadratic Equations
This section explores the fundamental concepts of linear and quadratic equations, their properties, and methods for solving them.
Worked Examples
Q1
Find the real roots of the equation:
- \( \frac{9}{x^4} + \frac{8}{x^2} = 1 \)
Solution:
- Let \( y = \frac{1}{x^2} \). Then the equation becomes:
\( 9y^2 + 8y - 1 = 0 \)
- Solve the quadratic equation using the quadratic formula:
\( y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)
where \( a = 9 \), \( b = 8 \), and \( c = -1 \).
- Substitute the values:
\( y = \frac{-8 \pm \sqrt{8^2 - 4(9)(-1)}}{18} \)
- Simplify:
\( y = \frac{-8 \pm \sqrt{64 + 36}}{18} = \frac{-8 \pm \sqrt{100}}{18} = \frac{-8 \pm 10}{18} \)
- The two possible values for \( y \) are:
\( y = \frac{1}{9} \) or \( y = -1 \)
- For \( y = \frac{1}{9} \), \( x^2 = 9 \), so \( x = \pm 3 \). There are no real solutions for \( y = -1 \).
- Therefore, the real roots are \( x = 3 \) and \( x = -3 \).
Q2
Solve the equation:
- \( x^4 - 13x^2 + 36 = 0 \)
Solution:
- Let \( y = x^2 \). Then the equation becomes:
\( y^2 - 13y + 36 = 0 \)
- Solve the quadratic equation:
\( y = \frac{13 \pm 5}{2} \)
- The solutions are \( y = 9 \) and \( y = 4 \).
- For \( y = 9 \), \( x = \pm 3 \); for \( y = 4 \), \( x = \pm 2 \).
- Therefore, the real roots are \( x = \pm 3 \) and \( x = \pm 2 \).
Q3
Find the real roots of the equation:
- \( x^2 - 2 = \frac{8}{x^2} \)
Solution:
- Multiply both sides by \( x^2 \):
\( x^4 - 2x^2 - 8 = 0 \)
- Let \( y = x^2 \), so the equation becomes:
\( y^2 - 2y - 8 = 0 \)
- Solve the quadratic equation:
\( y = \frac{2 \pm 6}{2} \)
- The real solutions are \( y = 4 \), leading to \( x = \pm 2 \). There are no real solutions for \( y = -2 \).
- Therefore, the real roots are \( x = 2 \) and \( x = -2 \).
Worked Examples
Q1
The curve \( y = 2 \sqrt{x} \) and the line \( 3y = x + 8 \) intersect at the points A and B.
a) Write down an equation satisfied by the x-coordinate of A and B.
Solution:
- From the line equation \( 3y = x + 8 \), solve for \( y \):
\[
y = \frac{x + 8}{3}
\]
- Substitute \( y = \frac{x + 8}{3} \) into the curve equation \( y = 2\sqrt{x} \):
\[
\frac{x + 8}{3} = 2\sqrt{x}
\]
- Multiply both sides by 3 to eliminate the fraction:
\[
x + 8 = 6\sqrt{x}
\]
- Square both sides to eliminate the square root:
\[
(x + 8)^2 = 36x
\]
- Expand the left-hand side:
\[
x^2 + 16x + 64 = 36x
\]
- Rearrange the equation to form a quadratic equation:
\[
x^2 - 20x + 64 = 0
\]
b) Solve the equation in part (a) and find the x-coordinates of A and B.
Solution:
- Solve the quadratic equation using the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
where \( a = 1 \), \( b = -20 \), and \( c = 64 \).
- Substitute the values:
\[
x = \frac{20 \pm \sqrt{(-20)^2 - 4(1)(64)}}{2(1)}
\]
\[
x = \frac{20 \pm \sqrt{400 - 256}}{2}
\]
\[
x = \frac{20 \pm \sqrt{144}}{2}
\]
\[
x = \frac{20 \pm 12}{2}
\]
- The two possible values of \( x \) are:
\[
x = \frac{20 + 12}{2} = 16 \quad \text{or} \quad x = \frac{20 - 12}{2} = 4
\]
- Therefore, the x-coordinates of A and B are \( x = 16 \) and \( x = 4 \).
c) Find the length of the line AB.
Solution:
- The length of the line AB is the distance between the x-coordinates of A and B:
\[
\text{Length of AB} = 16 - 4 = 12
\]
- Therefore, the length of the line AB is 12 units.
Q2
The graph shows that \( y = ax^2 + bx + c \), for \( x \geq 0 \). The graph crosses the x-axis at the points \( (1, 0) \) and \( \left(\frac{49}{4}, 0\right) \) and meets the y-axis at the point \( (0, 7) \).
Find the value of \( a \), the value of \( b \), and the value of \( c \).
Solution:
- The general equation is \( y = ax^2 + bx + c \).
- Since the graph meets the y-axis at \( (0, 7) \), we know that:
\[
c = 7
\]
- Substitute \( (1, 0) \) into the equation \( y = ax^2 + bx + c \):
\[
0 = a(1)^2 + b(1) + 7
\]
\[
0 = a + b + 7
\]
\[
a + b = -7 \quad \text{(Equation 1)}
\]
- Substitute \( \left(\frac{49}{4}, 0\right) \) into the equation:
\[
0 = a\left(\frac{49}{4}\right)^2 + b\left(\frac{49}{4}\right) + 7
\]
\[
0 = a\left(\frac{2401}{16}\right) + b\left(\frac{49}{4}\right) + 7
\]
\[
0 = \frac{2401a}{16} + \frac{49b}{4} + 7
\]
- Multiply the entire equation by 16 to eliminate the fractions:
\[
0 = 2401a + 196b + 112
\]
\[
2401a + 196b = -112 \quad \text{(Equation 2)}
\]
- Solve the system of equations:
- Equation 1: \( a + b = -7 \)
- Equation 2: \( 2401a + 196b = -112 \)
- Multiply Equation 1 by 196:
\[
196a + 196b = -1372
\]
- Subtract this from Equation 2:
\[
(2401a + 196b) - (196a + 196b) = -112 - (-1372)
\]
\[
2205a = 1260
\]
\[
a = \frac{1260}{2205} = \frac{4}{7}
\]
- Substitute \( a = \frac{4}{7} \) into Equation 1:
\[
\frac{4}{7} + b = -7
\]
\[
b = -7 - \frac{4}{7} = -\frac{53}{7}
\]
- Therefore, the values are \( a = \frac{4}{7} \), \( b = -\frac{53}{7} \), and \( c = 7 \).
Exploring Unique and Thought-Provoking Knowledge
This section explores questions from various fields that provide deep insights and an intellectual edge.
Worked Examples
Q1
What was the primary reason for the collapse of the Bronze Age civilizations around 1200 BCE?
Solution:
- The collapse is attributed to a combination of factors, including natural disasters, invasions by the Sea Peoples, internal social upheavals, and a breakdown in trade networks.
- This disrupted the supply of tin and copper necessary for making bronze, leading to the downfall of major civilizations such as the Mycenaeans, Hittites, and Egyptians.
Q2
What is the "Ship of Theseus" paradox, and what does it question about identity?
Solution:
- The "Ship of Theseus" paradox asks whether a ship that has had all its components replaced remains fundamentally the same ship.
- This paradox challenges the concept of identity, questioning whether an object that undergoes gradual change can still be considered the same object.
Q3
What is Gödel's Incompleteness Theorem, and how does it impact mathematical systems?
Solution:
- Gödel's Incompleteness Theorem states that in any consistent mathematical system, there are statements that are true but cannot be proven within that system.
- This means that no mathematical system can be both complete and consistent, implying that some truths will always lie beyond formal proof.
Q4
What is the "Fermi Paradox," and what does it question about extraterrestrial life?
Solution:
- The Fermi Paradox questions why, despite the high probability of extraterrestrial life, we have not yet encountered any evidence of other civilizations.
- This paradox highlights the apparent contradiction between the vastness of the universe and the lack of observational evidence of alien life.
Q5
What is the Sapir-Whorf Hypothesis, and how does it influence our understanding of language and thought?
Solution:
- The Sapir-Whorf Hypothesis posits that the structure of a language influences its speakers' cognition and worldview.
- It suggests that people who speak different languages perceive and think about the world differently because language shapes thought processes.
Q6
What is the "Red Queen Hypothesis," and how does it relate to evolutionary biology?
Solution:
- The Red Queen Hypothesis suggests that organisms must constantly adapt and evolve to survive in an ever-changing environment where other species are also evolving.
- This concept emphasizes continuous evolutionary arms races between species.
Q7
What is the significance of Göbekli Tepe, and how does it challenge traditional views of human civilization?
Solution:
- Göbekli Tepe is significant because it predates the advent of agriculture and permanent settlements.
- This challenges the traditional view that complex societies developed only after the establishment of agriculture and suggests that organized religion and monumental architecture may have preceded farming.
Q8
What is the "Dunning-Kruger Effect," and how does it influence people's perception of their abilities?
Solution:
- The Dunning-Kruger Effect is a cognitive bias in which people with low ability or knowledge overestimate their competence, while those with high competence tend to underestimate their abilities.
- This effect highlights the lack of self-awareness in individuals regarding their own skills.
Q9
What is the "Paradox of Thrift," and how does it relate to macroeconomic theory?
Solution:
- The Paradox of Thrift suggests that while saving money is beneficial for individuals, if everyone saves more during a recession, overall demand will fall, leading to lower total savings and a weaker economy.
- This paradox illustrates the conflict between individual rationality and collective outcomes in economics.
Q10
What is the significance of the "Arnolfini Portrait" by Jan van Eyck, and what are its key symbolic elements?
Solution:
- The "Arnolfini Portrait" is significant for its intricate detail and use of symbolism.
- Key elements include the mirror reflecting the scene, the dog symbolizing loyalty, and the use of light to create depth and realism, often interpreted as a visual contract or depiction of marriage.
Linear and Quadratic Equations-Vocabulary List
This section explores all of the Basic Vocabulary required to understand the topic.
Definitions
Linear Equation: A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable. The general form of a linear equation is \( ax + b = 0 \).
Quadratic Equation: A quadratic equation is an equation of the second degree, meaning it contains at least one term that is squared. The general form of a quadratic equation is \( ax^2 + bx + c = 0 \).
Vocabulary List
- General Form: The standard format of an equation, such as \( ax + b = 0 \) for linear equations and \( ax^2 + bx + c = 0 \) for quadratic equations.
- Solution: The value(s) of the variable that satisfy the equation.
- Constant: A fixed value that does not change.
- Variable: A symbol, usually a letter, that represents an unknown value.
- Factoring: The process of breaking down a quadratic equation into simpler expressions that multiply together to give the original equation.
- Quadratic Formula: A formula that provides the solutions to a quadratic equation.
- Discriminant: The expression under the square root in the quadratic formula, which determines the nature of the roots.
- Roots: The solutions to a quadratic equation; also known as zeros of the equation.
- Real Roots: The solutions to a quadratic equation that are real numbers.
- Complex Roots: The solutions to a quadratic equation that are complex numbers.
- Isolating: The process of rearranging an equation to get the variable of interest by itself on one side of the equation.
- Degree of an Equation: The highest power of the variable in the equation.
- Binomial: An algebraic expression containing two terms.
- Factorization: The process of breaking down an expression into a product of simpler expressions.
- Real-Life Application: The use of mathematical concepts, such as equations, to solve problems in everyday situations.
- Parabola: The graphical representation of a quadratic equation, showing the curve created by the equation.
- Intercept: The point where the graph of an equation crosses an axis.
- Standard Form: A specific arrangement of an equation or expression, particularly used in quadratic equations as \( ax^2 + bx + c = 0 \).
- Negative Discriminant: Indicates that a quadratic equation has no real roots but has two complex roots.
- Positive Discriminant: Indicates that a quadratic equation has two distinct real roots.
- Zero Discriminant: Indicates that a quadratic equation has exactly one real root, which is a repeated root.
- Vertex: The highest or lowest point on the graph of a parabola, representing the maximum or minimum value of the quadratic function.
- Axis of Symmetry: The vertical line that divides the parabola into two mirror-image halves, typically given by \( x = -\frac{b}{2a} \) for a quadratic equation.
Quadratic Equations-Completing the Square technique
Worked Examples
Q1
Given: \( y = -(x - 5)^2 + 3 \)
Solution:
- This is in the form \( y = a(x - h)^2 + k \), where the vertex is \( (h, k) \).
- Here, \( h = 5 \) and \( k = 3 \).
- Therefore, the vertex is:
\[
(5, 3)
\]
Q2
Given: \( y = -2(x - 1)^2 + 7 \)
Solution:
- This is in the form \( y = a(x - h)^2 + k \), where the vertex is \( (h, k) \).
- Here, \( h = 1 \) and \( k = 7 \).
- Therefore, the vertex is:
\[
(1, 7)
\]
Q3
Given: \( y = 5(x + 1)^2 + 6 \)
Solution:
- This is in the form \( y = a(x - h)^2 + k \), where the vertex is \( (h, k) \).
- Here, \( h = -1 \) and \( k = 6 \).
- Therefore, the vertex is:
\[
(-1, 6)
\]
Q4
Given: \( y = 3(x + 4)^2 + 10 \)
Solution:
- This is in the form \( y = a(x - h)^2 + k \), where the vertex is \( (h, k) \).
- Here, \( h = -4 \) and \( k = 10 \).
- Therefore, the vertex is:
\[
(-4, 10)
\]
Q5
Given: \( y = -5(x + 8)^2 - 1 \)
Solution:
- This is in the form \( y = a(x - h)^2 + k \), where the vertex is \( (h, k) \).
- Here, \( h = -8 \) and \( k = -1 \).
- Therefore, the vertex is:
\[
(-8, -1)
\]
Q6
Given: \( y = (x + 2)^2 - 5 \)
Solution:
- This is in the form \( y = a(x - h)^2 + k \), where the vertex is \( (h, k) \).
- Here, \( h = -2 \) and \( k = -5 \).
- Therefore, the vertex is:
\[
(-2, -5)
\]
Q7
Express \( 7 + 5x - x^2 \) in the form \( a - (x + b)^2 \)
Given: \( 7 + 5x - x^2 \)
Solution:
- Rearrange the equation so that the quadratic term is first:
\[
-x^2 + 5x + 7
\]
- Factor out the negative sign from the quadratic and linear terms:
\[
-(x^2 - 5x) + 7
\]
- To complete the square, take half of the coefficient of \( x \), square it, and add and subtract it inside the parentheses. Half of \(-5\) is \(-\frac{5}{2}\), and squaring this gives \(\frac{25}{4}\):
\[
-(x^2 - 5x + \frac{25}{4} - \frac{25}{4}) + 7
\]
- Simplify the expression inside the parentheses:
\[
-( (x - \frac{5}{2})^2 - \frac{25}{4}) + 7
\]
- Distribute the negative sign and simplify:
\[
-(x - \frac{5}{2})^2 + \frac{25}{4} + 7
\]
- Combine the constants:
\[
a = \frac{25}{4} + 7 = \frac{25}{4} + \frac{28}{4} = \frac{53}{4}
\]
- So, the expression in the desired form is:
\[
\frac{53}{4} - (x - \frac{5}{2})^2
\]
Q8
Express \( 2x^2 + 9x + 4 \) in the form \( a(x + b)^2 + c \)
Given: \( 2x^2 + 9x + 4 \)
Solution:
- Factor out the 2 from the quadratic and linear terms:
\[
2(x^2 + \frac{9}{2}x) + 4
\]
- To complete the square, take half of the coefficient of \( x \), square it, and add and subtract it inside the parentheses. Half of \(\frac{9}{2}\) is \(\frac{9}{4}\), and squaring this gives \(\frac{81}{16}\):
\[
2\left(x^2 + \frac{9}{2}x + \frac{81}{16} - \frac{81}{16}\right) + 4
\]
- Simplify the expression inside the parentheses:
\[
2\left((x + \frac{9}{4})^2 - \frac{81}{16}\right) + 4
\]
- Distribute the 2 and simplify:
\[
2(x + \frac{9}{4})^2 - \frac{81}{8} + 4
\]
- Combine the constants:
\[
a = 2, \quad b = \frac{9}{4}, \quad c = 4 - \frac{81}{8} = \frac{32}{8} - \frac{81}{8} = -\frac{49}{8}
\]
- So, the expression in the desired form is:
\[
2(x + \frac{9}{4})^2 - \frac{49}{8}
\]
Worked Examples
Q1 (Find the Vertex and Axis of Symmetry for \( f(x) = x^2 + 8x - 1 \))
Given: \( f(x) = x^2 + 8x - 1 \)
Solution:
- Complete the square:
\[
f(x) = x^2 + 8x + \left(\frac{8}{2}\right)^2 - \left(\frac{8}{2}\right)^2 - 1
= (x + 4)^2 - 17
\]
- The vertex is \( (-4, -17) \).
- The formula for the axis of symmetry is \( x = -\frac{b}{2a} \). For this equation, \( a = 1 \) and \( b = 8 \), so:
\[
x = -\frac{8}{2(1)} = -4
\]
- The axis of symmetry is \( x = -4 \).
Q2 (Find the Vertex and Axis of Symmetry for \( f(x) = x^2 + 10x + 25 \))
Given: \( f(x) = x^2 + 10x + 25 \)
Solution:
- Recognize that this is a perfect square:
\[
f(x) = (x + 5)^2
\]
- The vertex is \( (-5, 0) \).
- Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = 1 \) and \( b = 10 \):
\[
x = -\frac{10}{2(1)} = -5
\]
- The axis of symmetry is \( x = -5 \).
Q3 (Find the Vertex and Axis of Symmetry for \( f(x) = -x^2 + 2x + 5 \))
Given: \( f(x) = -x^2 + 2x + 5 \)
Solution:
- Factor out the negative sign and complete the square:
\[
f(x) = -\left(x^2 - 2x + 1 - 1 + 5\right) = -(x - 1)^2 + 6
\]
- The vertex is \( (1, 6) \).
- Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -1 \) and \( b = 2 \):
\[
x = -\frac{2}{2(-1)} = 1
\]
- The axis of symmetry is \( x = 1 \).
Q4 (Find the Vertex and Axis of Symmetry for \( f(x) = -2x^2 - 8x - 3 \))
Given: \( f(x) = -2x^2 - 8x - 3 \)
Solution:
- Factor out the -2 and complete the square:
\[
f(x) = -2\left(x^2 + 4x + 4 - 4 - \frac{3}{2}\right) = -2(x + 2)^2 + 5
\]
- The vertex is \( (-2, 5) \).
- Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -2 \) and \( b = -8 \):
\[
x = -\frac{-8}{2(-2)} = -2
\]
- The axis of symmetry is \( x = -2 \).
Q5 (Find the Vertex and Axis of Symmetry for \( y = -x^2 + 10x - 34 \))
Given: \( y = -x^2 + 10x - 34 \)
Solution:
- Complete the square:
\[
y = -(x^2 - 10x + 25 - 25 - 34) = -(x - 5)^2 - 9
\]
- The vertex is \( (5, -9) \).
- Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -1 \) and \( b = 10 \):
\[
x = -\frac{10}{2(-1)} = 5
\]
- The axis of symmetry is \( x = 5 \).
Q6 (Find the Vertex and Axis of Symmetry for \( y = -x^2 - 6x + 1 \))
Given: \( y = -x^2 - 6x + 1 \)
Solution:
- Complete the square:
\[
y = -(x^2 + 6x + 9 - 9 + 1) = -(x + 3)^2 + 10
\]
- The vertex is \( (-3, 10) \).
- Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -1 \) and \( b = -6 \):
\[
x = -\frac{-6}{2(-1)} = -3
\]
- The axis of symmetry is \( x = -3 \).
Q7 (Find the Vertex and Axis of Symmetry for \( y = -4x^2 + 12x - 7 \))
Given: \( y = -4x^2 + 12x - 7 \)
Solution:
- Factor out the -4 and complete the square:
\[
y = -4(x^2 - 3x + \frac{9}{4} - \frac{9}{4} - 7) = -4(x - \frac{3}{2})^2 + 2
\]
- The vertex is \( \left(\frac{3}{2}, 2\right) \).
- Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -4 \) and \( b = 12 \):
\[
x = -\frac{12}{2(-4)} = \frac{3}{2}
\]
- The axis of symmetry is \( x = \frac{3}{2} \).
Q8: Find the Vertex and Axis of Symmetry for \( y = -9x^2 + 6x + 2 \)
Given: \( y = -9x^2 + 6x + 2 \)
Solution:
- Factor out the -9 and complete the square:
\[
y = -9(x^2 - \frac{2}{3}x + \frac{1}{9} - \frac{1}{9} + 2) = -9(x - \frac{1}{3})^2 + 3
\]
- The vertex is \( \left(\frac{1}{3}, 3\right) \).
- Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -9 \) and \( b = 6 \):
\[
x = -\frac{6}{2(-9)} = \frac{1}{3}
\]
- The axis of symmetry is \( x = \frac{1}{3} \).
Q9: Find the Vertex and Axis of Symmetry for \( y = 4x^2 - 1 \)
Given: \( y = 4x^2 - 1 \)
Solution:
- This is already a perfect square form:
\[
y = 4(x)^2 - 1
\]
- The vertex is \( (0, -1) \).
- Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = 4 \) and \( b = 0 \):
\[
x = 0
\]
- The axis of symmetry is \( x = 0 \).
Q10: Find the Vertex and Axis of Symmetry for \( y = x^2 - 16 \)
Given: \( y = x^2 - 16 \)
Solution:
- This is already a perfect square form:
\[
y = (x)^2 - 16
\]
- The vertex is \( (0, -16) \).
- Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = 1 \) and \( b = 0 \):
\[
x = 0
\]
- The axis of symmetry is \( x = 0 \).
Quadratic Equations-finding a and b
Worked Examples
Q1 (Write \( y = 4x^2 + 8x - 5 \) in the form \( y = a(x + b)^2 + c \), where \( a \), \( b \), and \( c \) are integers)
Given: \( y = 4x^2 + 8x - 5 \)
Solution:
- First, factor out the coefficient of \( x^2 \) from the first two terms:
\[
y = 4(x^2 + 2x) - 5
\]
- Now complete the square by adding and subtracting the square of half the coefficient of \( x \). Half of 2 is 1, and \( 1^2 = 1 \):
\[
y = 4\left(x^2 + 2x + 1 - 1\right) - 5
\]
- Simplify the expression:
\[
y = 4\left((x + 1)^2 - 1\right) - 5
\]
- Distribute the 4:
\[
y = 4(x + 1)^2 - 4 - 5
\]
- Combine the constants:
\[
y = 4(x + 1)^2 - 9
\]
- Thus, the quadratic function in the form \( y = a(x + b)^2 + c \) is:
\[
y = 4(x + 1)^2 - 9
\]
where \( a = 4 \), \( b = 1 \), and \( c = -9 \).
Intersection of a Quadratic Curve and a Line
Q2 (Find any points of intersection between the curve \( C \) and the line \( l \))
Given:
- Curve \( C \) has the equation \( y = x^2 - 3x + 2 \).
- Line \( l \) has the equation \( y = 3x - 7 \).
Solution:
- To find the points of intersection, set the equations for the curve and the line equal to each other:
\[
x^2 - 3x + 2 = 3x - 7
\]
- Rearrange the equation to form a standard quadratic equation:
\[
x^2 - 3x - 3x + 2 + 7 = 0 \implies x^2 - 6x + 9 = 0
\]
- Factor the quadratic equation:
\[
(x - 3)^2 = 0
\]
- Solving for \( x \), we get:
\[
x = 3
\]
- Substitute \( x = 3 \) back into the equation of the line to find the corresponding value of \( y \):
\[
y = 3(3) - 7 = 9 - 7 = 2
\]
- Therefore, the point of intersection is \( (3, 2) \).
Quadratic Equations-Conditions for No Real Roots
Worked Examples
Q1: Show that \( p^2 < 12q \) for the equation \( y = 3x^2 + 2px + 4q \) having no real roots
Given: \( y = 3x^2 + 2px + 4q \)
Solution:
- The general condition for a quadratic equation to have no real roots is that the discriminant must be less than zero. The discriminant \( \Delta \) of a quadratic equation \( ax^2 + bx + c = 0 \) is given by:
\[
\Delta = b^2 - 4ac
\]
- For the given equation \( y = 3x^2 + 2px + 4q \), the coefficients are:
\[
a = 3, \quad b = 2p, \quad c = 4q
\]
- Substituting these values into the discriminant formula:
\[
\Delta = (2p)^2 - 4(3)(4q) = 4p^2 - 48q
\]
- For the equation to have no real roots, the discriminant must be less than zero:
\[
4p^2 - 48q < 0
\]
- Simplifying the inequality:
\[
4p^2 < 48q
\]
Dividing both sides by 4:
\[
p^2 < 12q
\]
- Thus, we have shown that \( p^2 < 12q \).
Q2: Find the minimum value of the function \( f(x) = x^2 + 4x + c \), giving your answer in terms of \( c \)
Given: \( f(x) = x^2 + 4x + c \)
Solution:
- To find the minimum value of the function, we complete the square.
- First, factor the quadratic and linear terms:
\[
f(x) = (x^2 + 4x) + c
\]
- Complete the square by adding and subtracting the square of half the coefficient of \( x \). Half of 4 is 2, and \( 2^2 = 4 \):
\[
f(x) = (x^2 + 4x + 4 - 4) + c = (x + 2)^2 - 4 + c
\]
- The minimum value of \( (x + 2)^2 \) occurs when \( (x + 2)^2 = 0 \). Therefore, the minimum value of the function is:
\[
f(x) = -4 + c
\]
- Thus, the minimum value of the function is \( c - 4 \), and it occurs when \( x = -2 \).
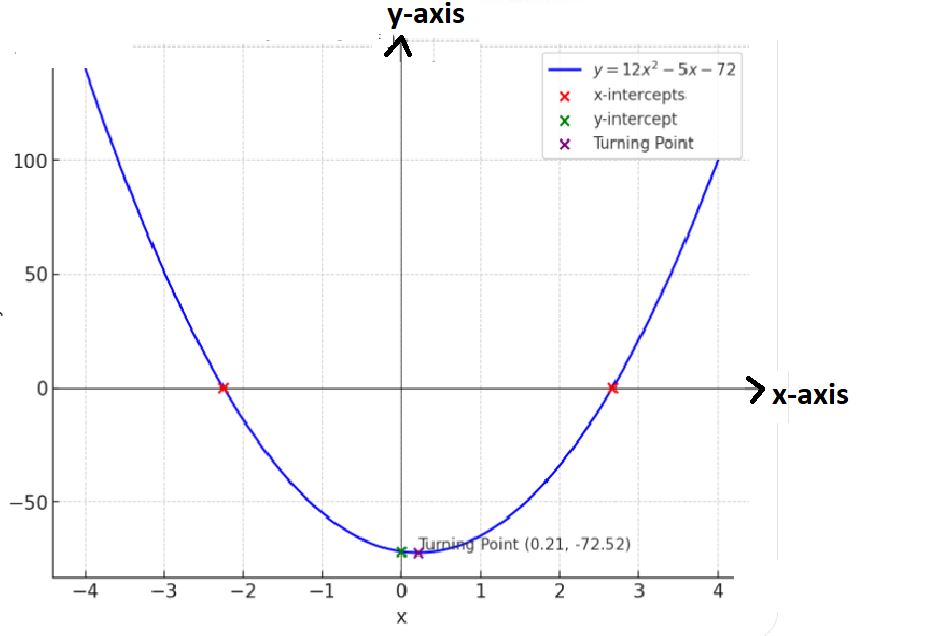
Q3: Sketch the graph of \( y = 12x^2 - 5x - 72 \), labelling any points where the graph crosses the coordinate axes and the turning point
Given: \( y = 12x^2 - 5x - 72 \)
Solution:
- To sketch the graph, we need to find:
- The x-intercepts (roots of the quadratic)
- The y-intercept (value of \( y \) when \( x = 0 \))
- The turning point (vertex of the parabola)
Step 1: Find the x-intercepts
- To find the x-intercepts, set \( y = 0 \) and solve the quadratic equation:
\[
12x^2 - 5x - 72 = 0
\]
- We can use the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
where \( a = 12 \), \( b = -5 \), and \( c = -72 \).
- Substituting the values:
\[
x = \frac{-(-5) \pm \sqrt{(-5)^2 - 4(12)(-72)}}{2(12)}
= \frac{5 \pm \sqrt{25 + 3456}}{24}
= \frac{5 \pm \sqrt{3481}}{24}
= \frac{5 \pm 59}{24}
\]
- This gives two solutions:
\[
x = \frac{5 + 59}{24} = \frac{64}{24} = \frac{8}{3}, \quad x = \frac{5 - 59}{24} = \frac{-54}{24} = -\frac{9}{4}
\]
- Therefore, the x-intercepts are \( x = \frac{8}{3} \) and \( x = -\frac{9}{4} \).
Step 2: Find the y-intercept
- To find the y-intercept, set \( x = 0 \):
\[
y = 12(0)^2 - 5(0) - 72 = -72
\]
- The y-intercept is \( y = -72 \).
Step 3: Find the turning point
- We can find the turning point using the formula for the vertex \( x = -\frac{b}{2a} \). For the given equation, \( a = 12 \) and \( b = -5 \):
\[
x = -\frac{-5}{2(12)} = \frac{5}{24}
\]
- Substitute \( x = \frac{5}{24} \) into the equation to find the corresponding \( y \)-value:
\[
y = 12\left(\frac{5}{24}\right)^2 - 5\left(\frac{5}{24}\right) - 72
\]
Simplifying this will give the value of \( y \) at the turning point.
Quadratic Equations-Completing the Square and Finding Turning Points
Worked Examples
Q1: Find the minimum value of \( x^2 - 7x + 8 \) and the corresponding value of \( x \)
Given: \( f(x) = x^2 - 7x + 8 \)
Solution:
- Complete the square to express the quadratic in the form \( a(x + b)^2 + c \):
\[
f(x) = x^2 - 7x + 8 = \left(x - \frac{7}{2}\right)^2 - \frac{49}{4} + 8
\]
Now simplify:
\[
f(x) = \left(x - \frac{7}{2}\right)^2 - \frac{49}{4} + \frac{32}{4} = \left(x - \frac{7}{2}\right)^2 - \frac{17}{4}
\]
- The minimum value occurs when \( \left(x - \frac{7}{2}\right)^2 = 0 \). This gives the minimum value of:
\[
f(x) = -\frac{17}{4}
\]
- The corresponding value of \( x \) is \( x = \frac{7}{2} \).
- Thus, the minimum value is \( -\frac{17}{4} \), and it occurs at \( x = \frac{7}{2} \).
Q2: Find the turning point of \( y = 7 + 5x - x^2 \) and determine if it is a maximum or minimum
Given: \( y = 7 + 5x - x^2 \)
Solution:
- Rearrange the equation to recognize the quadratic term:
\[
y = -x^2 + 5x + 7
\]
- Complete the square to express the quadratic in the form \( a(x + b)^2 + c \):
\[
y = -\left(x^2 - 5x + \frac{25}{4} - \frac{25}{4} + 7\right) = -\left(x - \frac{5}{2}\right)^2 + \frac{49}{4}
\]
- The vertex is \( \left(\frac{5}{2}, \frac{49}{4}\right) \).
- Since the coefficient of \( x^2 \) is negative, the parabola opens downwards, and thus the turning point is a maximum point.
- Therefore, the turning point is at \( \left(\frac{5}{2}, \frac{49}{4}\right) \), and it is a maximum point.
Worked Examples
Q1 (Jun 2006, Q6)
Solve the inequality \( x^2 + 2x < 3 \).
Solution:
- Rearrange the inequality to standard quadratic form:
\[
x^2 + 2x - 3 < 0
\]
- Factorize the quadratic expression:
\[
(x + 3)(x - 1) < 0
\]
- Determine the critical points, where \( x + 3 = 0 \) or \( x - 1 = 0 \):
\[
x = -3 \quad \text{and} \quad x = 1
\]
- Analyze the sign of \( (x + 3)(x - 1) \) in the intervals defined by the critical points \( x = -3 \) and \( x = 1 \):
- For \( x < -3 \), both factors are negative, so the product is positive.
- For \( -3 < x < 1 \), \( x + 3 \) is positive and \( x - 1 \) is negative, so the product is negative.
- For \( x > 1 \), both factors are positive, so the product is positive.
- The inequality holds in the interval where the product is negative:
\[
-3 < x < 1
\]
Q2 (Jun 2009, Q4)
Solve the inequality \( x(x - 6) > 0 \).
Solution:
- Find the critical points by solving \( x(x - 6) = 0 \):
\[
x = 0 \quad \text{or} \quad x = 6
\]
- Analyze the sign of \( x(x - 6) \) in the intervals defined by \( x = 0 \) and \( x = 6 \):
- For \( x < 0 \), both \( x \) and \( x - 6 \) are negative, so the product is positive.
- For \( 0 < x < 6 \), \( x \) is positive and \( x - 6 \) is negative, so the product is negative.
- For \( x > 6 \), both \( x \) and \( x - 6 \) are positive, so the product is positive.
- The inequality holds where the product is positive:
\[
x < 0 \quad \text{or} \quad x > 6
\]
Q3 (Jan 2010, Q2)
Solve the inequality \( \frac{5x - 3}{2} \leq x + 5 \).
Solution:
- First, eliminate the fraction by multiplying both sides by 2:
\[
5x - 3 \leq 2(x + 5)
\]
- Expand the right-hand side:
\[
5x - 3 \leq 2x + 10
\]
- Move all terms involving \( x \) to one side and constants to the other side:
\[
5x - 2x \leq 10 + 3
\]
\[
3x \leq 13
\]
- Divide both sides by 3:
\[
x \leq \frac{13}{3}
\]
- Thus, the solution is:
\[
x \leq \frac{13}{3}
\]
Q4 (Jan 2013, Q4)
Solve the inequality \( 5x^2 - 28x - 12 \leq 0 \).
Solution:
- First, solve the equation \( 5x^2 - 28x - 12 = 0 \) using the quadratic formula:
\[
x = \frac{-(-28) \pm \sqrt{(-28)^2 - 4(5)(-12)}}{2(5)}
\]
\[
x = \frac{28 \pm \sqrt{784 + 240}}{10}
\]
\[
x = \frac{28 \pm \sqrt{1024}}{10}
\]
\[
x = \frac{28 \pm 32}{10}
\]
- The two solutions are:
\[
x = \frac{28 + 32}{10} = 6 \quad \text{or} \quad x = \frac{28 - 32}{10} = -0.4
\]
- So the critical points are \( x = -0.4 \) and \( x = 6 \).
- Analyze the sign of \( 5x^2 - 28x - 12 \) in the intervals defined by these critical points:
- For \( x < -0.4 \), the expression is positive.
- For \( -0.4 \leq x \leq 6 \), the expression is non-positive.
- For \( x > 6 \), the expression is positive.
- Thus, the solution is:
\[
-0.4 \leq x \leq 6
\]
Q5 (Jun 2014, Q6)
Solve the inequality \( 3x^2 + 10x + 3 > 0 \).
Solution:
- First, solve the equation \( 3x^2 + 10x + 3 = 0 \) using the quadratic formula:
\[
x = \frac{-10 \pm \sqrt{(10)^2 - 4(3)(3)}}{2(3)}
\]
\[
x = \frac{-10 \pm \sqrt{100 - 36}}{6}
\]
\[
x = \frac{-10 \pm \sqrt{64}}{6}
\]
\[
x = \frac{-10 \pm 8}{6}
\]
- The two solutions are:
\[
x = \frac{-10 + 8}{6} = \frac{-2}{6} = -\frac{1}{3} \quad \text{or} \quad x = \frac{-10 - 8}{6} = \frac{-18}{6} = -3
\]
- So the critical points are \( x = -3 \) and \( x = -\frac{1}{3} \).
- Analyze the sign of \( 3x^2 + 10x + 3 \) in the intervals defined by these critical points:
- For \( x < -3 \), the expression is positive.
- For \( -3 < x < -\frac{1}{3} \), the expression is negative.
- For \( x > -\frac{1}{3} \), the expression is positive.
- Thus, the solution is:
\[
x < -3 \quad \text{or} \quad x > -\frac{1}{3}
\]
Q7 (OCR 4721, Jun 2005, Q8)
The length of a rectangular children’s playground is 10 m more than its width. The width of the playground is \( x \) meters.
(i) The perimeter of the playground is greater than 64 m. Write down a linear inequality in \( x \).
Solution:
- The length is \( x + 10 \) meters.
- The perimeter of a rectangle is given by:
\[
\text{Perimeter} = 2(\text{Length} + \text{Width}) = 2(x + x + 10) = 4x + 20
\]
- Set up the inequality for the perimeter:
\[
4x + 20 > 64
\]
- Simplify the inequality:
\[
4x > 44 \quad \Rightarrow \quad x > 11
\]
(ii) The area of the playground is less than 299 m². Show that \( (x - 13)(x + 23) < 0 \).
Solution:
- The area of a rectangle is given by:
\[
\text{Area} = \text{Length} \times \text{Width} = (x + 10)x = x^2 + 10x
\]
- Set up the inequality for the area:
\[
x^2 + 10x < 299
\]
- Rearrange the inequality to standard quadratic form:
\[
x^2 + 10x - 299 < 0
\]
- Factorize the quadratic expression:
\[
(x - 13)(x + 23) < 0
\]
(iii) By solving the inequalities in parts (i) and (ii), determine the set of possible values of \( x \).
Solution:
- From part (i), \( x > 11 \).
- From part (ii), \( -23 < x < 13 \).
- Combining these two results, the set of possible values of \( x \) is:
\[
11 < x < 13
\]
Worked Examples
Q1 (Jun 2010, Q7)
Solve the simultaneous equations:
- \( x + 2y - 6 = 0 \)
- \( 2x^2 + y^2 = 57 \)
Solution:
- From the first equation, solve for \( x \) in terms of \( y \):
\[
x = 6 - 2y
\]
- Substitute \( x = 6 - 2y \) into the second equation:
\[
2(6 - 2y)^2 + y^2 = 57
\]
- Expand and simplify:
\[
2(36 - 24y + 4y^2) + y^2 = 57
\]
\[
72 - 48y + 8y^2 + y^2 = 57
\]
\[
9y^2 - 48y + 72 = 57
\]
\]
\[
9y^2 - 48y + 15 = 0
\]
- Solve the quadratic equation using the quadratic formula:
\[
y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
where \( a = 9 \), \( b = -48 \), and \( c = 15 \).
- Substitute the values:
\[
y = \frac{48 \pm \sqrt{(-48)^2 - 4(9)(15)}}{2(9)}
\]
\[
y = \frac{48 \pm \sqrt{2304 - 540}}{18}
\]
\[
y = \frac{48 \pm \sqrt{1764}}{18}
\]
\[
y = \frac{48 \pm 42}{18}
\]
- Thus, the two solutions for \( y \) are:
\[
y = \frac{48 + 42}{18} = \frac{90}{18} = 5 \quad \text{or} \quad y = \frac{48 - 42}{18} = \frac{6}{18} = \frac{1}{3}
\]
- For \( y = 5 \), substitute into \( x = 6 - 2y \):
\[
x = 6 - 2(5) = -4
\]
- For \( y = \frac{1}{3} \), substitute into \( x = 6 - 2y \):
\[
x = 6 - 2\left(\frac{1}{3}\right) = 6 - \frac{2}{3} = \frac{16}{3}
\]
- Thus, the solutions are:
\[
(x, y) = (-4, 5) \quad \text{or} \quad \left(\frac{16}{3}, \frac{1}{3}\right)
\]
Q2 (Jun 2011, Q4)
Solve the simultaneous equations:
- \( y = 2(x - 2)^2 \)
- \( 3x + y = 26 \)
Solution:
- Substitute \( y = 2(x - 2)^2 \) into the second equation:
\[
3x + 2(x - 2)^2 = 26
\]
- Expand and simplify:
\[
3x + 2(x^2 - 4x + 4) = 26
\]
\[
3x + 2x^2 - 8x + 8 = 26
\]
\[
2x^2 - 5x + 8 = 26
\]
\[
2x^2 - 5x - 18 = 0
\]
- Solve the quadratic equation using the quadratic formula:
\[
x = \frac{-(-5) \pm \sqrt{(-5)^2 - 4(2)(-18)}}{2(2)}
\]
\[
x = \frac{5 \pm \sqrt{25 + 144}}{4}
\]
\[
x = \frac{5 \pm \sqrt{169}}{4}
\]
\[
x = \frac{5 \pm 13}{4}
\]
- Thus, the two solutions for \( x \) are:
\[
x = \frac{5 + 13}{4} = \frac{18}{4} = 4.5 \quad \text{or} \quad x = \frac{5 - 13}{4} = \frac{-8}{4} = -2
\]
- For \( x = 4.5 \), substitute into \( y = 2(x - 2)^2 \):
\[
y = 2(4.5 - 2)^2 = 2(2.5)^2 = 2(6.25) = 12.5
\]
- For \( x = -2 \), substitute into \( y = 2(x - 2)^2 \):
\[
y = 2(-2 - 2)^2 = 2(-4)^2 = 2(16) = 32
\]
- Thus, the solutions are:
\[
(x, y) = (4.5, 12.5) \quad \text{or} \quad (-2, 32)
\]
Q3 (Jan 2013, Q4)
(i) Solve the simultaneous equations:
- \( y = 2x^2 - 3x - 5 \)
- \( 10x + 2y + 11 = 0 \)
Solution:
- Substitute \( y = 2x^2 - 3x - 5 \) into the second equation:
\[
10x + 2(2x^2 - 3x - 5) + 11 = 0
\]
- Expand and simplify:
\[
10x + 4x^2 - 6x - 10 + 11 = 0
\]
\[
4x^2 + 4x + 1 = 0
\]
- Factorize the quadratic equation:
\[
(2x + 1)^2 = 0
\]
\li>Solve for \( x \):
\[
2x + 1 = 0 \quad \Rightarrow \quad x = -\frac{1}{2}
\]
- Substitute \( x = -\frac{1}{2} \) into \( y = 2x^2 - 3x - 5 \):
\[
y = 2\left(\frac{-1}{2}\right)^2 - 3\left(\frac{-1}{2}\right) - 5 = 2\left(\frac{1}{4}\right) + \frac{3}{2} - 5 = \frac{1}{2} + \frac{3}{2} - 5 = -3
\]
- Thus, the solution is:
\[
(x, y) = \left( -\frac{1}{2}, -3 \right)
\]
(ii) What can you deduce from the answer to part (i) about the curve \( y = 2x^2 - 3x - 5 \) and the line \( 10x + 2y + 11 = 0 \)?
Solution:
- The curve and the line intersect at exactly one point, \( \left( -\frac{1}{2}, -3 \right) \), which means the line is a tangent to the curve at this point.
Q4 (Jun 2015, Q6)
Solve the simultaneous equations:
- \( 2x + y - 5 = 0 \)
- \( x^2 - y^2 = 3 \)
Solution:
- From the first equation, solve for \( y \) in terms of \( x \):
\[
y = 5 - 2x
\]
- Substitute \( y = 5 - 2x \) into the second equation:
\[
x^2 - (5 - 2x)^2 = 3
\]
- Expand and simplify:
\[
x^2 - (25 - 20x + 4x^2) = 3
\]
\[
x^2 - 25 + 20x - 4x^2 = 3
\]
\[
-3x^2 + 20x - 28 = 0
\]
\li>Multiply through by \(-1\):
\[
3x^2 - 20x + 28 = 0
\]
- Solve the quadratic equation using the quadratic formula:
\[
x = \frac{-(-20) \pm \sqrt{(-20)^2 - 4(3)(28)}}{2(3)}
\]
- Solve the quadratic equation using the quadratic formula:
\[
x = \frac{-(-20) \pm \sqrt{(-20)^2 - 4(3)(28)}}{2(3)}
\]
\[
x = \frac{20 \pm \sqrt{400 - 336}}{6}
\]
\[
x = \frac{20 \pm \sqrt{64}}{6}
\]
\[
x = \frac{20 \pm 8}{6}
\]
- Thus, the two solutions for \( x \) are:
- For the positive root:
\[
x = \frac{20 + 8}{6} = \frac{28}{6} = \frac{14}{3}
\]
- For the negative root:
\[
x = \frac{20 - 8}{6} = \frac{12}{6} = 2
\]
- For \( x = \frac{14}{3} \), substitute into \( y = 5 - 2x \):
\[
y = 5 - 2\left(\frac{14}{3}\right) = 5 - \frac{28}{3} = \frac{15}{3} - \frac{28}{3} = -\frac{13}{3}
\]
- For \( x = 2 \), substitute into \( y = 5 - 2x \):
\[
y = 5 - 2(2) = 5 - 4 = 1
\]
- Thus, the solutions are:
\[
(x, y) = \left(\frac{14}{3}, -\frac{13}{3}\right) \quad \text{or} \quad (2, 1)
\]
Q5 (Jun 2016, Q3)
Solve the simultaneous equations:
- \( x^2 + y^2 = 34 \)
- \( 3x - y + 4 = 0 \)
Solution:
- From the second equation, solve for \( y \) in terms of \( x \):
\[
y = 3x + 4
\]
- Substitute \( y = 3x + 4 \) into the first equation:
\[
x^2 + (3x + 4)^2 = 34
\]
- Expand and simplify:
\[
x^2 + (9x^2 + 24x + 16) = 34
\]
\[
10x^2 + 24x + 16 = 34
\]
\[
10x^2 + 24x - 18 = 0
\]
- Simplify by dividing through by 2:
\[
5x^2 + 12x - 9 = 0
\]
- Solve the quadratic equation using the quadratic formula:
\[
x = \frac{-12 \pm \sqrt{(12)^2 - 4(5)(-9)}}{2(5)}
\]
\[
x = \frac{-12 \pm \sqrt{144 + 180}}{10}
\]
\[
x = \frac{-12 \pm \sqrt{324}}{10}
\]
\[
x = \frac{-12 \pm 18}{10}
\]
- Thus, the two solutions for \( x \) are:
- For the positive root:
\[
x = \frac{-12 + 18}{10} = \frac{6}{10} = 0.6
\]
- For the negative root:
\[
x = \frac{-12 - 18}{10} = \frac{-30}{10} = -3
\]
- For \( x = 0.6 \), substitute into \( y = 3x + 4 \):
\[
y = 3(0.6) + 4 = 1.8 + 4 = 5.8
\]
- For \( x = -3 \), substitute into \( y = 3x + 4 \):
\[
y = 3(-3) + 4 = -9 + 4 = -5
\]
- Thus, the solutions are:
\[
(x, y) = (0.6, 5.8) \quad \text{or} \quad (-3, -5)
\]
Worked Examples
Question No:1
Solve the equation:
- \( \frac{x^{2002} + 4x^{2001}}{4x^{2000}} = 2449.25 \)
Solution:
- Start by multiplying both sides by 4 to eliminate the denominator:
\[
\frac{x^{2002} + 4x^{2001}}{x^{2000}} = 9797
\]
- Factor out \( x^{2000} \) from the numerator:
\[
\frac{x^{2000}(x^2 + 4x)}{x^{2000}} = 9797
\]
- Cancel \( x^{2000} \) from both sides, leading to:
\[
x^2 + 4x = 9797
\]
- Rearrange the equation:
\[
x^2 + 4x - 9797 = 0
\]
- Solve the quadratic equation using the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
where \( a = 1 \), \( b = 4 \), and \( c = -9797 \).
- Substitute the values:
\[
x = \frac{-4 \pm \sqrt{4^2 - 4(1)(-9797)}}{2(1)} = \frac{-4 \pm \sqrt{16 + 39188}}{2} = \frac{-4 \pm \sqrt{39204}}{2}
\]
- Simplify:
\[
x = \frac{-4 \pm 198}{2}
\]
- The two possible solutions are:
\[
x = \frac{-4 + 198}{2} = 97 \quad \text{or} \quad x = \frac{-4 - 198}{2} = -101
\]
- Thus, the roots of the equation are \( x = 97 \) and \( x = -101 \).
Question No: 2
Ben opened his history book and noticed that the product of the two pages in front of him was equal to 1122. What were the numbers of those pages?
Solution:
- Let the first page be \( n \). The next page is \( n + 1 \).
- The product of the pages is given by:
\[
n(n + 1) = 1122
\]
- Expand the equation:
\[
n^2 + n = 1122
\]
- Move all terms to the left-hand side:
\[
n^2 + n - 1122 = 0
\]
- Solve the quadratic equation by factoring:
\[
(n + 34)(n - 33) = 0
\]
- Set each factor to zero:
\[
n + 34 = 0 \quad \text{or} \quad n - 33 = 0
\]
Hence, \( n = -34 \) or \( n = 33 \).
- Since a page number cannot be negative, \( n = 33 \) is the only valid solution.
- The two pages are \( n = 33 \) and \( n + 1 = 34 \).
Question No: 3
Worked Examples
Find the value of the following expression:
- \( \sqrt{6 + \sqrt{6 + \sqrt{6 + \cdots}}} \)
Solution:
- Let \( x \) be the value of the expression, so we can write:
\[
x = \sqrt{6 + \sqrt{6 + \sqrt{6 + \cdots}}}.
\]
- This simplifies to:
\[
x = \sqrt{6 + x}.
\]
- Square both sides to remove the square root:
\[
x^2 = 6 + x.
\]
- Rearrange the equation to form a quadratic equation:
\[
x^2 - x - 6 = 0.
\]
- Factor the quadratic equation:
\[
(x - 3)(x + 2) = 0.
\]
- Solve for \( x \):
\[
x - 3 = 0 \quad \Rightarrow \quad x = 3,
\]
\[
x + 2 = 0 \quad \Rightarrow \quad x = -2.
\]
- Since \( x \) must be greater than 0 (because it represents the value inside a square root), the valid solution is \( x = 3 \).
- Thus, the value of the expression is:
\[
\sqrt{6 + \sqrt{6 + \sqrt{6 + \cdots}}} = 3.
\]
Understanding Maximum and Minimum Values of a Quadratic Function
1. General Form
The quadratic function is represented as \( f(x) = ax^2 + bx + c \), where \( a, b, \) and \( c \) are constants and \( a \neq 0 \).
2. Shape of the Graph
The graph of a quadratic function is a parabola. The direction (upward or downward) depends on the sign of \( a \):
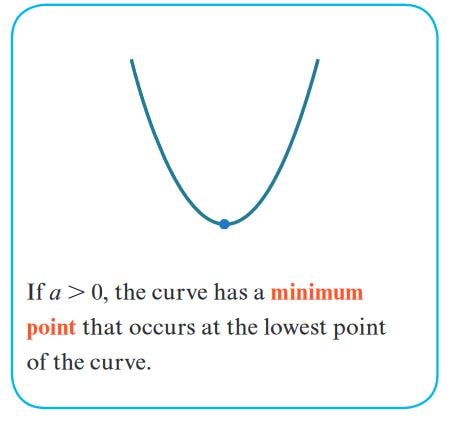
- If \( a > 0 \), parabola opens upwards (minimum point at vertex).
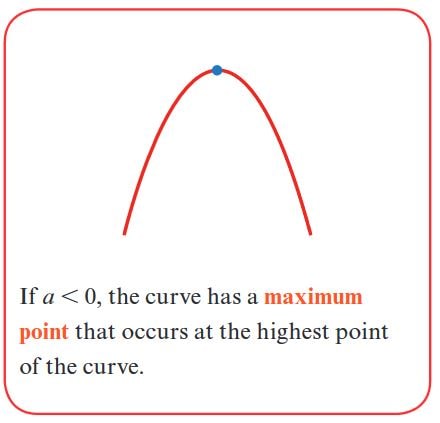
- If \( a < 0 \), parabola opens downwards (maximum point at vertex).
3. Finding the Vertex
The vertex (h, k) can be found using:
- \( h = -\frac{b}{2a} \)
- \( k = f(h) \)
4. Vertex Form of a Quadratic Function
Rewrite the function in vertex form: \( f(x) = a(x-h)^2 + k \)
5. Determining Maximum or Minimum Values
Based on the coefficient \( a \):
- Minimum Value: If \( a > 0 \), \( f(x) \) has a minimum at \( x = h \), value \( k \).
- Maximum Value: If \( a < 0 \), \( f(x) \) has a maximum at \( x = h \), value \( k \).
6. Examples
Question No: 1
Worked Examples
Find the vertex and minimum value of the following quadratic function:
- \( f(x) = 2x^2 - 4x + 1 \)
Solution:
- First, identify the general form of a quadratic function:
\[
f(x) = ax^2 + bx + c.
\]
- For the given function \( f(x) = 2x^2 - 4x + 1 \), we have:
\[
a = 2, \quad b = -4, \quad c = 1.
\]
- The x-coordinate of the vertex can be found using the formula:
\[
x = -\frac{b}{2a}.
\]
- Substituting the values of \( a \) and \( b \):
\[
x = -\frac{-4}{2 \times 2} = \frac{4}{4} = 1.
\]
- Thus, the x-coordinate of the vertex is \( x = 1 \).
- Next, find the y-coordinate (minimum value) by substituting \( x = 1 \) into the original function:
\[
f(1) = 2(1)^2 - 4(1) + 1 = 2 - 4 + 1 = -1.
\]
- Thus, the vertex is at \( (1, -1) \), and the minimum value of the function is \( -1 \).
Question No: 2
Worked Examples
Find the vertex and maximum value of the following quadratic function:
- \( f(x) = -x^2 + 6x - 8 \)
Solution:
- The given function is \( f(x) = -x^2 + 6x - 8 \). Here:
\[
a = -1, \quad b = 6, \quad c = -8.
\]
- The x-coordinate of the vertex is given by the formula:
\[
x = -\frac{b}{2a}.
\]
- Substituting the values of \( a \) and \( b \):
\[
x = -\frac{6}{2 \times -1} = \frac{6}{-2} = 3.
\]
- Thus, the x-coordinate of the vertex is \( x = 3 \).
- Next, find the y-coordinate (maximum value) by substituting \( x = 3 \) into the original function:
\[
f(3) = -(3)^2 + 6(3) - 8 = -9 + 18 - 8 = 1.
\]
- Thus, the vertex is at \( (3, 1) \), and the maximum value of the function is \( 1 \).
For \( f(x) = -x^2 + 6x - 8 \), the vertex is at \( x = 3 \), maximum value is \( 1 \).
7. Applications
Quadratic functions are used in scenarios like projectile motion, economics, and architectural designs.


