Differentiation Concepts Explained

Notation

There are three different notations commonly used to describe the derivative of a function:

• If \( y = x^2 \), then \( \frac{dy}{dx} = 2x \).
• If \( f(x) = x^2 \), then \( f'(x) = 2x \).
• \( \frac{d}{dx}(x^2) = 2x \).

The derivative \( \frac{dy}{dx} \) is called the derivative of \( y \) with respect to \( x \). \( f'(x) \) is the derivative of \( f(x) \), sometimes referred to as the gradient function of this curve, indicating the slope of the tangent to the curve at any point.

Differentiation of Power Functions

The power rule for differentiation is given by:

\[ \frac{d}{dx}(x^n) = nx^{n-1} \]

This rule applies to any real power \( n \), not only for positive integers.

Examples

• \( \frac{d}{dx}(x^4) = 4x^3 \)
• \( \frac{d}{dx}(x^5) = 5x^4 \)
• \( \frac{d}{dx}(x^6) = 6x^5 \)

Key Point 7.1

The general rule for differentiating power functions is:

\[ \frac{d}{dx}(x^n) = nx^{n-1} \]

Find the Derivative of Each of the Following

• \( x^7 \): \( \frac{d}{dx}(x^7) = 7x^6 \)
• \( \frac{1}{x^2} \): Rewrite as \( x^{-2} \), then \( \frac{d}{dx}(x^{-2}) = -2x^{-3} = -\frac{2}{x^3} \)
• \( \sqrt{x} \): Rewrite as \( x^{1/2} \), then \( \frac{d}{dx}(x^{1/2}) = \frac{1}{2}x^{-1/2} = \frac{1}{2\sqrt{x}} \)
• \( y = 2 \): The derivative of a constant is zero.

Detailed Solutions for Differentiation

Example 1: Differentiating a Polynomial and Rational Function

Function: \( f(x) = 3x^4 - \frac{1}{2x^2} + \frac{4}{\sqrt{x}} + 5 \)

Differentiation:

\[ f'(x) = \frac{d}{dx}(3x^4) - \frac{d}{dx}\left(\frac{1}{2x^2}\right) + \frac{d}{dx}\left(\frac{4}{x^{1/2}}\right) + \frac{d}{dx}(5) \]

\[ = 12x^3 + \frac{1}{x^3} - \frac{2}{\sqrt{x^3}} \]

Example 2: Gradient of the Tangent to the Curve

Function: \( y = x(2x-1)(x+3) \)

Expanded: \( y = 2x^3 + 5x^2 - 3x \)

Differentiate: \( \frac{dy}{dx} = 6x^2 + 10x - 3 \)

At \( x = 1 \): \( \frac{dy}{dx} = 6(1)^2 + 10(1) - 3 = 13 \)

Gradient at \( (1, 4) \) is 13.

Example 3: Coefficients of a Polynomial

Function: \( y = ax^4 + bx^2 + x \)

Differentiate: \( \frac{dy}{dx} = 4ax^3 + 2bx + 1 \)

Given gradients:

\( 4a(1)^3 + 2b(1) + 1 = 3 \)

\( 4a(-2)^3 + 2b(-2) + 1 = -51 \)

Solving these equations:

\( 4a + 2b = 2 \)

\( -32a - 4b = -52 \)

\( a = 2, b = -3 \)

Gradient Calculations

Example a: y = x^4 at (1, 1) results in dy/dx = 4.

Example b: y = x^2 - 2x + 3 at (0, 3) results in dy/dx = -2.

Differentiation of Functions

Example a: \( y = x^5 \) results in \( dy/dx = 5x^4 \).

Example b: \( y = x^9 \) results in \( dy/dx = 9x^8 \).

Example c: \( y = \frac{1}{x} \) results in \( dy/dx = -\frac{1}{x^2} \).

Derivatives for Given Functions

Example a: \( f(x) = 2x^4 \) results in \( f'(x) = 8x^3 \).

Example b: \( f(x) = 3x^5 \) results in \( f'(x) = 15x^4 \).

Derivatives at Specific Points

Example a: \( y = x^2 + x - 4 \) at (1, -2) results in \( dy/dx = 3 \).

Example b: \( y = 5 - \frac{2}{x} \) at (2, 4) results in \( dy/dx = \frac{1}{2} \).

Detailed Solutions for Differentiation

Finding Gradients and Differentiating Functions

Example a: \( y = x^4 \) at \( (1, 1) \), gradient: \( \frac{dy}{dx} = 4x^3 \rightarrow 4 \).

Example b: \( y = x^2 - 2x + 3 \) at \( (0, 3) \), gradient: \( \frac{dy}{dx} = 2x - 2 \rightarrow -2 \).

Basic Differentiation

Example a: \( x^5 \), derivative: \( \frac{dx^5}{dx} = 5x^4 \).

Example b: \( x^9 \), derivative: \( \frac{dx^9}{dx} = 9x^8 \).

Example c: \( x^{-4} \), derivative: \( \frac{dx^{-4}}{dx} = -4x^{-5} = -\frac{4}{x^5} \).

Example d: \( \frac{1}{x} \), derivative: \( \frac{d}{dx}(\frac{1}{x}) = -\frac{1}{x^2} \).

Complex Function Differentiation

Example e: \( \frac{5}{3x^2} \), derivative: \( \frac{d}{dx}(\frac{5}{3x^2}) = -\frac{10}{3x^3} \).

Example f: \( -2 \), derivative: \( \frac{d}{dx}(-2) = 0 \).

Example g: \( \frac{4x}{\sqrt{x}} \), derivative: \( \frac{d}{dx}(4\sqrt{x}) = 2\sqrt{x} \).

Example h: \( \frac{2x}{3x^3} \), derivative: \( \frac{d}{dx}(\frac{2}{3x^2}) = -\frac{4}{3x^3} \).

Differentiating Polynomial and Rational Functions

Example g: \( y = 7x^2 - \frac{3}{x} + \frac{2}{x^2} \), derivative: \( \frac{dy}{dx} = 14x + \frac{3}{x^2} - \frac{4}{x^3} \).

Example h: \( y = 3x + \frac{5}{x} - \frac{1}{\sqrt{x}} \), derivative: \( \frac{dy}{dx} = 3 - \frac{5}{x^2} + \frac{1}{2x^{3/2}} \).

Example i: \( y = 4x^2 + 3x - \frac{2}{\sqrt{x}} \), derivative: \( \frac{dy}{dx} = 8x + 3 + \frac{1}{x^{3/2}} \).

Further Problems with solutions

Problem 1: Coordinates of Points on the Curve

\( y = x^3 - 3x - 8 \) with gradient 9. Solutions: Points \((2, -9)\) and \((-2, -2)\).

Problem 2: Gradient at x-axis Crossing

Gradient at \( x = 2 \) for \( y = \frac{5x - 10}{x^2} \) is 1.25.

Problem 3: Intersection Points and Gradients

Points A and B: \((3, -8)\) and \((-2, 7)\).

Problem 4: Gradient for Quadratic Equation

\( y = ax^2 + bx \) at \( (3, -3) \), gradient is 5, solving for \( a \) and \( b \).

Problem 5: Derivative and Coefficients

\( y = x^3 + ax^2 + bx + 7 \) at \( (1, 5) \), gradient -5, solve for \( a \) and \( b \).

Chain Rule

Solution for the Curve Problem

The curve \( y = \sqrt{ax + b} \) passes through the point (12, 4) and has gradient \( \frac{1}{4} \) at this point. Find the value of \( a \) and the value of \( b \).

Given: \( y = \sqrt{ax + b} \), passes through \( (12, 4) \), gradient \( \frac{1}{4} \) at this point.

Start by substituting \( x = 12 \) and \( y = 4 \):

\[ 4 = \sqrt{12a + b} \quad \text{(1)} \]

Square both sides to eliminate the square root:

\[ 16 = 12a + b \quad \text{(rearranged from 1)} \]

Differentiate \( y = \sqrt{ax + b} \) with respect to \( x \) using the chain rule:

\[ \frac{dy}{dx} = \frac{a}{2\sqrt{ax + b}} \]

Set the derivative equal to the known gradient at \( x = 12 \):

\[ \frac{1}{4} = \frac{a}{2\sqrt{12a + b}} \quad \text{(2)} \]

Substitute \( b = 16 - 12a \) from (1) into (2) and solve for \( a \) and \( b \):

\[ \frac{1}{4} = \frac{a}{8} \Rightarrow a = 2, \quad b = -8 \text{ (from solving the system)} \]

Conclusion: \( a = 2 \), \( b = -8 \).

TextBook solutions

Differentiation Problems

1a. \( \frac{d}{dx}\left(x + 4\right)^6 = 6\left(x + 4\right)^5 \)

1b. \( \frac{d}{dx}\left(2x + 3\right)^8 = 16\left(2x + 3\right)^7 \)

1c. \( \frac{d}{dx}\left(3 - 4x\right)^5 = -20\left(3 - 4x\right)^4 \)

1d. \( \frac{d}{dx}\left(\frac{x}{2} + 1\right)^9 = \frac{9}{2}\left(\frac{x}{2} + 1\right)^8 \)

Tangents and Normals

Equations of Tangent and Normal Lines

Find the equation of the tangent and the normal to the curve \( y = 2x^2 + \frac{8}{x^2} - 9 \) at the point where \( x = 2 \).

Answer:

Given the function:

\[ y = 2x^2 + \frac{8}{x^2} - 9 \]

First, differentiate with respect to \( x \) to find \( \frac{dy}{dx} \):

\[ \frac{dy}{dx} = 4x - \frac{16}{x^3} \]

At \( x = 2 \), calculate \( y \) and \( \frac{dy}{dx} \):

\[ y = 2(2)^2 + \frac{8}{(2)^2} - 9 = 1 \]

\[ \frac{dy}{dx} = 4(2) - \frac{16}{(2)^3} = 6 \]

The equation of the tangent line at \( (2, 1) \) with a gradient of 6:

\[ y - 1 = 6(x - 2) \]

\[ y = 6x - 11 \]

The equation of the normal line at \( (2, 1) \) with a gradient of \( -\frac{1}{6} \):

\[ y - 1 = -\frac{1}{6}(x - 2) \]

\[ x + 6y = 8 \]

Question

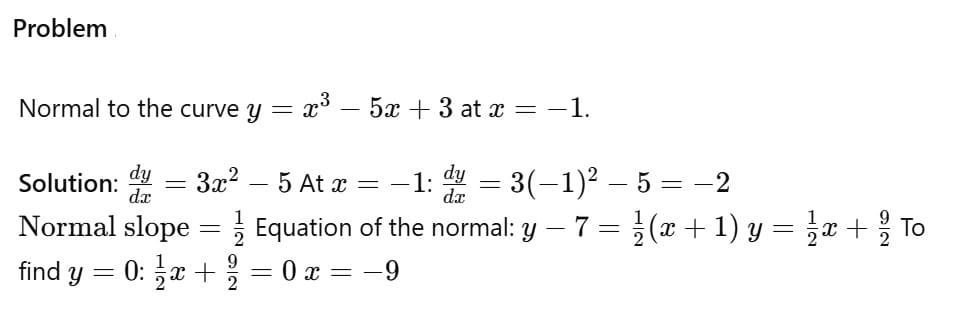
Worksheet 1: Basic Differentiation

Differentiate the following functions:

1. \( f(x) = 6x^5 \)


2. \( g(x) = 9x^3 - 4x \)


3. \( h(x) = x^2 + 3x + 7 \)


4. \( p(x) = 5 \)


5. \( q(x) = 8x^{-2} \)


6. \( r(x) = \sqrt{x} \)


7. \( s(x) = \frac{1}{x} \)


8. \( t(x) = x^{3/2} \)


9. \( u(x) = 3x^4 - 5x^2 + 6 \)


10. \( v(x) = 4x \)


11. \( w(x) = 7 \)


12. \( y(x) = 3x^3 - 2x + 4x^{-1} \)


13. \( z(x) = \frac{1}{\sqrt{x}} \)


14. \( a(x) = x^7 - 7x^3 + 5x \)


15. \( b(x) = 9x^{2/3} - 3x^{1/3} \)


16. \( c(x) = 5x^{1/4} \)


17. \( d(x) = 2x^2 + 5x^3 - x^{-3} \)


18. \( e(x) = \frac{2}{x^2} - 3x^4 \)


19. \( f(x) = x(x^2 + 1) \)


20. \( g(x) = (2x + 3)(x - 5) \)

Worksheet 2: Chain Rule

Differentiate the following functions using the chain rule:

1. \( f(x) = (3x+4)^5 \)


2. \( g(x) = \sqrt{5x-1} \)


3. \( h(x) = \left(\frac{x}{x+1}\right)^2 \)


4. \( p(x) = \sin(2x + 3) \)


5. \( q(x) = e^{2x-3} \)


6. \( r(x) = \ln(x^2 + 1) \)


7. \( s(x) = \cos^2(x) \)


8. \( t(x) = e^{x^2 + 2x} \)


9. \( u(x) = \tan(x + \frac{\pi}{4}) \)


10. \( v(x) = \sqrt{x^4 + 3x} \)


11. \( w(x) = (x^3 - x)^4 \)


12. \( y(x) = \ln(\sin x) \)


13. \( z(x) = e^{\sqrt{x}} \)


14. \( a(x) = (2x^2 - 3x + 4)^3 \)


15. \( b(x) = \sin^2(3x) \)


16. \( c(x) = \cos(x^2 + x) \)


17. \( d(x) = \tan^2(x + 2) \)


18. \( e(x) = \sqrt{\cos x} \)


19. \( f(x) = (5x + 3)^{1/2} \)


20. \( g(x) = \ln(x^3 + 2x) \)

Worksheet 3: Tangents and Normals

Determine the equations for the tangents and normals to the following functions at the given points:

1. \( y = x^3 - 4x \) at \( x = 2 \)


2. \( y = \sqrt{x} \) at \( x = 4 \)


3. \( y = \sin x \) at \( x = \frac{\pi}{4} \)


4. \( y = \ln(x) \) at \( x = e \)


5. \( y = e^{x} \) at \( x = 1 \)


6. \( y = \tan x \) at \( x = \frac{\pi}{4} \)


7. \( y = \frac{1}{x} \) at \( x = 1 \)


8. \( y = x^2 \) at \( x = -1 \)


9. \( y = 3x^3 - 5x + 1 \) at \( x = 0 \)


10. \( y = 4\sqrt{x} \) at \( x = 9 \)


11. \( y = \cos x \) at \( x = \frac{\pi}{3} \)


12. \( y = e^{-x} \) at \( x = 2 \)


13. \( y = \frac{x}{x+1} \) at \( x = 1 \)


14. \( y = \frac{1}{x^2} \) at \( x = 2 \)


15. \( y = x^4 - 2x^2 + x \) at \( x = 1 \)


16. \( y = \sqrt{x+1} \) at \( x = 0 \)


17. \( y = \frac{1}{\sqrt{x}} \) at \( x = 4 \)


18. \( y = x^3 \) at \( x = -2 \)


19. \( y = \ln(x^2 + 1) \) at \( x = 0 \)


20. \( y = \sin^2(x) \) at \( x = \frac{\pi}{6} \)