• Logo
  • Wk 1
  • Wk 2
  • Wk 3
  • Wk 4
  • Wk 5
  • Wk 6
  • Wk 7
  • Wk 8
  • Wk 9
  • Wk 10
  • Wk 11
  • wk 12-Asgn
  • wk 13-Mid-Term
  • wk 14-Sol
  • wk 15
  • HomeWork

Circular Measures Vocabulary

  • Week 6[Chapter 4-Circular Measures]

    • Circular Measure Notes

  • What is a Radian
  • Text Book Solutions
  • Worksheet
  • Circular Measure-Quiz
  • Past Papers

Circular Measure-Vocabulary List

Circular Measures Vocabulary

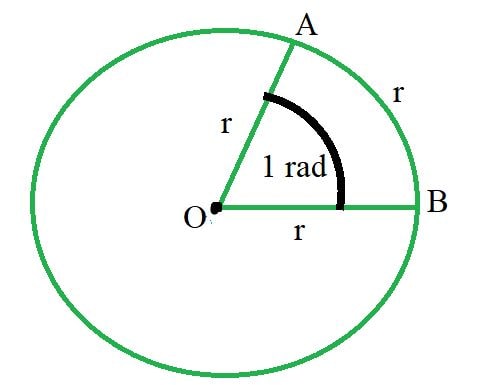
  • Radian: A unit of angle measure in which the angle is defined as the ratio of the length of the arc to the radius of the circle. One radian is the angle formed when the arc length is equal to the radius.
  • Degree: A unit of angle measure where one complete revolution around a circle is divided into 360 equal parts.
  • Conversion between Degrees and Radians: To convert from degrees to radians:

    \[ \text{Radians} = \text{Degrees} \times \frac{\pi}{180} \]

    To convert from radians to degrees:

    \[ \text{Degrees} = \text{Radians} \times \frac{180}{\pi} \]

  • Arc Length: The distance along the curved line making up the arc. For an angle \( \theta \) in radians and a circle with radius \( r \):

    \[ \text{Arc Length} = r \times \theta \]

  • Sector: A region of a circle bounded by two radii and the corresponding arc. It resembles a "slice" of the circle.
  • Area of a Sector: The area of a sector of a circle with angle \( \theta \) (in radians) and radius \( r \) is given by:

    \[ \text{Area of Sector} = \frac{1}{2} r^2 \theta \]

  • Central Angle: An angle whose vertex is the center of the circle and whose sides are radii of the circle. It is measured in degrees or radians.
  • Full Circle (in Radians): A complete revolution around a circle corresponds to \( 2\pi \) radians or \( 360^\circ \).
  • Semicircle: Half of a circle. The angle subtended by a semicircle is \( \pi \) radians or \( 180^\circ \).
  • Minor and Major Arcs: A minor arc is an arc smaller than a semicircle, and a major arc is larger than a semicircle. Together, they make up the entire circumference of the circle.
  • Sector Angle: The angle subtended by the arc of the sector at the center of the circle. It is measured in radians or degrees.
  • Perimeter of a Sector: The sum of the lengths of the two radii and the arc length:

    \[ \text{Perimeter} = 2r + r\theta \]

    (where \( \theta \) is in radians).
  • Segment of a Circle: A region bounded by a chord and the corresponding arc. There are two types: the minor segment (smaller) and the major segment (larger).
  • Area of a Segment: The area of a segment can be found by subtracting the area of the triangular part from the area of the sector:

    \[ \text{Area of Segment} = \frac{1}{2}r^2(\theta - \sin\theta) \]

    (where \( \theta \) is in radians).
  • Circular Arc: A portion of the circumference of a circle. The length of a circular arc is directly proportional to the central angle subtended.
  • Circular Sector: A portion of a circle enclosed by two radii and their intercepted arc. The area is proportional to the angle it subtends.
  • Chord: A line segment with both endpoints on the circle. A chord divides the circle into two arcs: the minor arc (smaller) and the major arc (larger).
  • Tangent: A line that touches the circle at exactly one point, called the point of tangency. A tangent is perpendicular to the radius at the point of tangency.
  • Secant: A line that intersects the circle at two distinct points. A secant contains a chord.
  • Sector Radius: The radius of the circle that forms the boundary of a sector. It is a line segment from the center of the circle to any point on the arc.
  • Angular Velocity: The rate of change of the angle (in radians) with respect to time. It is often used in rotational motion:

    \[ \omega = \frac{\theta}{t} \]

    where \( \omega \) is the angular velocity, \( \theta \) is the angle in radians, and \( t \) is the time.
  • Arc Measure: The measure of the angle subtended by the arc at the center of the circle, expressed in radians or degrees.
  • Inscribed Angle: An angle formed by two chords in a circle which have a common endpoint. The vertex of the angle is on the circle itself.
  • Relationship between Inscribed and Central Angles: The measure of an inscribed angle is half the measure of the central angle that subtends the same arc:

    \[ \text{Inscribed Angle} = \frac{1}{2} \times \text{Central Angle} \]

  • Length of a Chord: The length of a chord can be calculated using the radius and the angle subtended by the chord:

    \[ \text{Length of Chord} = 2r \sin\left(\frac{\theta}{2}\right) \]

    (where \( \theta \) is the angle in radians and \( r \) is the radius).
  • Angle at the Center: An angle formed by two radii of a circle. This angle is twice any inscribed angle subtending the same arc.

Past Papers

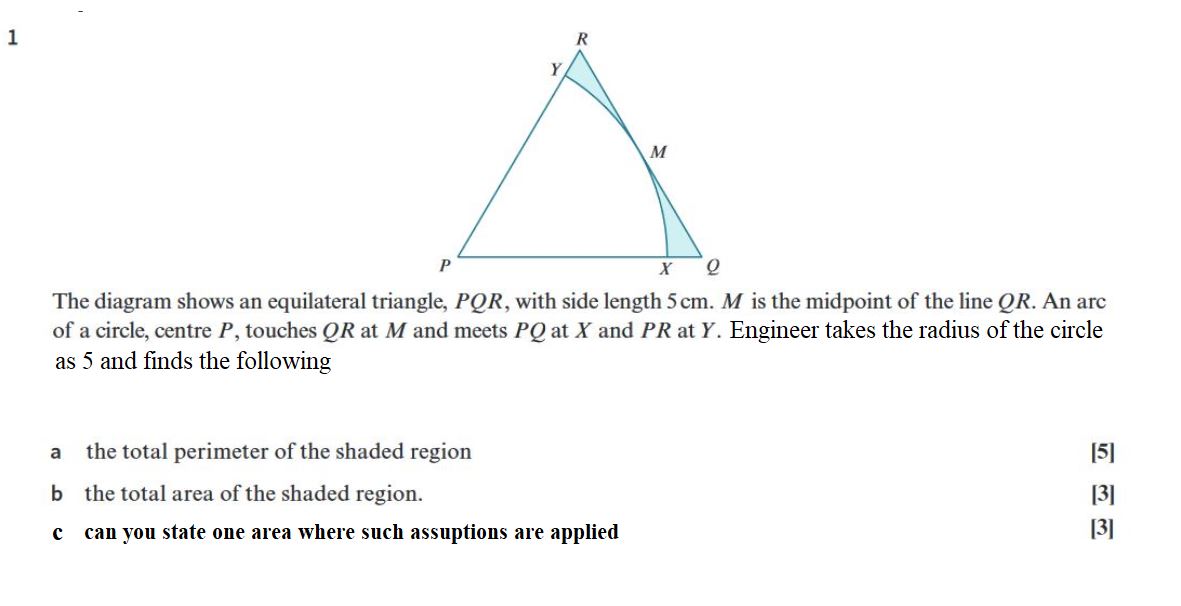
\[ \textbf{4. Finding the Perimeter of the Shaded Region} \] \[ 1. \text{Perimeter of the equilateral triangle } PQR: \] \[ \text{Each side of the triangle is } 5 \text{ cm}. \] \[ \text{Perimeter of } PQR = 5 + 5 + 5 = 15 \text{ cm} \] \[ 2. \text{Perimeter of the sector } PXMYP: \] \[ \text{The sector includes two radii (PX and PY) each of } 5 \text{ cm, and the arc } XY \text{ of } \frac{5\pi}{3} \text{ cm}. \] \[ \text{Perimeter of sector } PXMYP = 5 + \frac{5\pi}{3} + 5 = 10 + \frac{5\pi}{3} \text{ cm} \] \[ 3. \text{Perimeter of the shaded region:} \] \[ \text{Perimeter of shaded region} = \text{Perimeter of } PQR - (\text{Perimeter of sector } PXMYP) + \text{Arc } XY \] \[ = 15 - \left(10 + \frac{5\pi}{3}\right) + \frac{5\pi}{3} \] \[ = 15 - 10 \] \[ = 5 \text{ cm} \] \[ \textbf{The total perimeter of the shaded region is } 5 \text{ cm}. \]
Note:
Explanation:

Application of Guess and Check Methodology in Diverse Fields

The approach of an engineer assuming the radius of a circle to be 5 units, when juxtaposed with the dimensions of a side of an equilateral triangle, may initially seem mathematically imprecise or abstract. However, this practice aligns with the broader mathematical strategy known as "guess and check" or "trial and testing," methodologies that are fundamental not only in mathematical problem-solving but also extensively utilized in fields such as pharmacology, game design, and virtual reality.


Justification and Broader Implications:

Guess and Check in Mathematical Context:

This method involves making an initial guess, testing this guess against the given conditions, and adjusting it based on the outcome. This iterative process is similar to the approach taken in the problem where an initial assumption about the circle's radius is tested against geometric constraints.


Applications in Pharmacology:

In drug development, the "trial and testing" approach is pivotal. Researchers hypothesize about drug interactions, dosages, or therapeutic effects and test these hypotheses through clinical trials. The initial assumptions (guesses) are rigorously tested and refined based on empirical data, mirroring the iterative nature of refining the circle's radius in the geometric problem.


Relevance to Cartoon Movies, Animation Graphics, Game Design and Virtual Reality:

In game design and virtual reality, developers often create and adjust virtual environments and character proportions based on what is visually and interactively effective. The example of Popeye with disproportionately large arms illustrates this concept vividly. Designers "guess" dimensions that might enhance the character's appeal or functionality and "check" these in the game's setting to gauge player reception and usability.


The acceptance of exaggerated features in characters like Popeye underscores a key principle in virtual design: reality can be altered for thematic emphasis or narrative engagement, much like how geometric dimensions can be theoretically adjusted for illustrative purposes.


Understanding Acceptable Deviations:

Just as pharmacologists need to determine acceptable limits for drug efficacy and safety, game developers must decide on the extent of deviation from realistic proportions that remains acceptable to players. This decision is often guided by user feedback, testing sessions, and market trends, similar to how mathematical assumptions are refined based on theoretical consistency and practical application.


The question of "how much is acceptable" is central to both fields. In gaming and VR, this often translates to determining the threshold at which a feature or design becomes immersive rather than distracting. This balance is crucial for maintaining the suspension of disbelief essential in engaging digital experiences.


Conclusion:

The assumption by the engineer of using a 5-unit circle radius in a problem setup, though seemingly abstract, serves as a practical example of the application of guess-and-check methodologies. These methodologies are not only foundational in mathematical reasoning but also extend their utility to diverse fields like pharmacology and digital media design. They facilitate innovative solutions and creative designs that push the boundaries of conventional approaches, ultimately enhancing user engagement and satisfaction in digital environments.


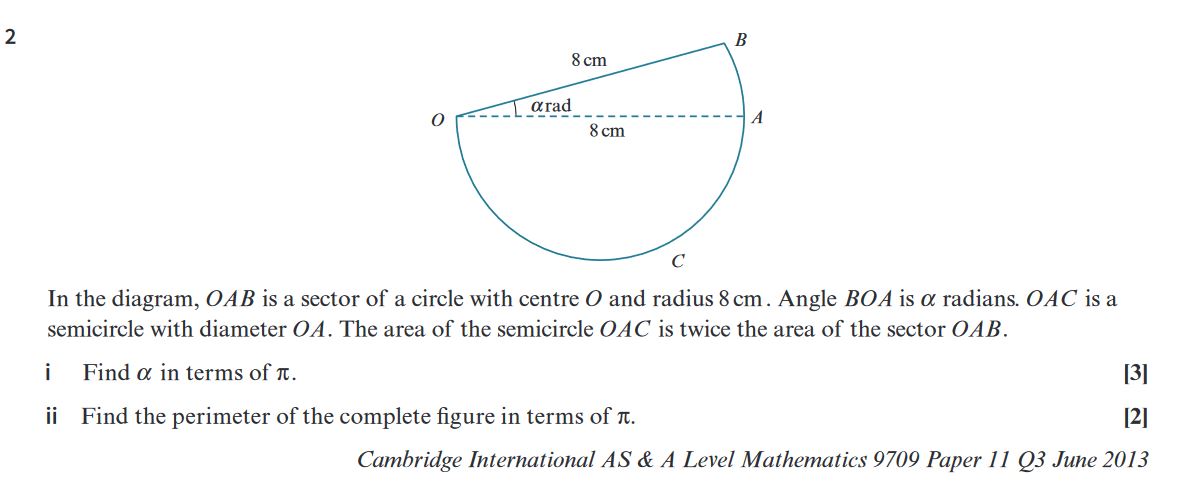
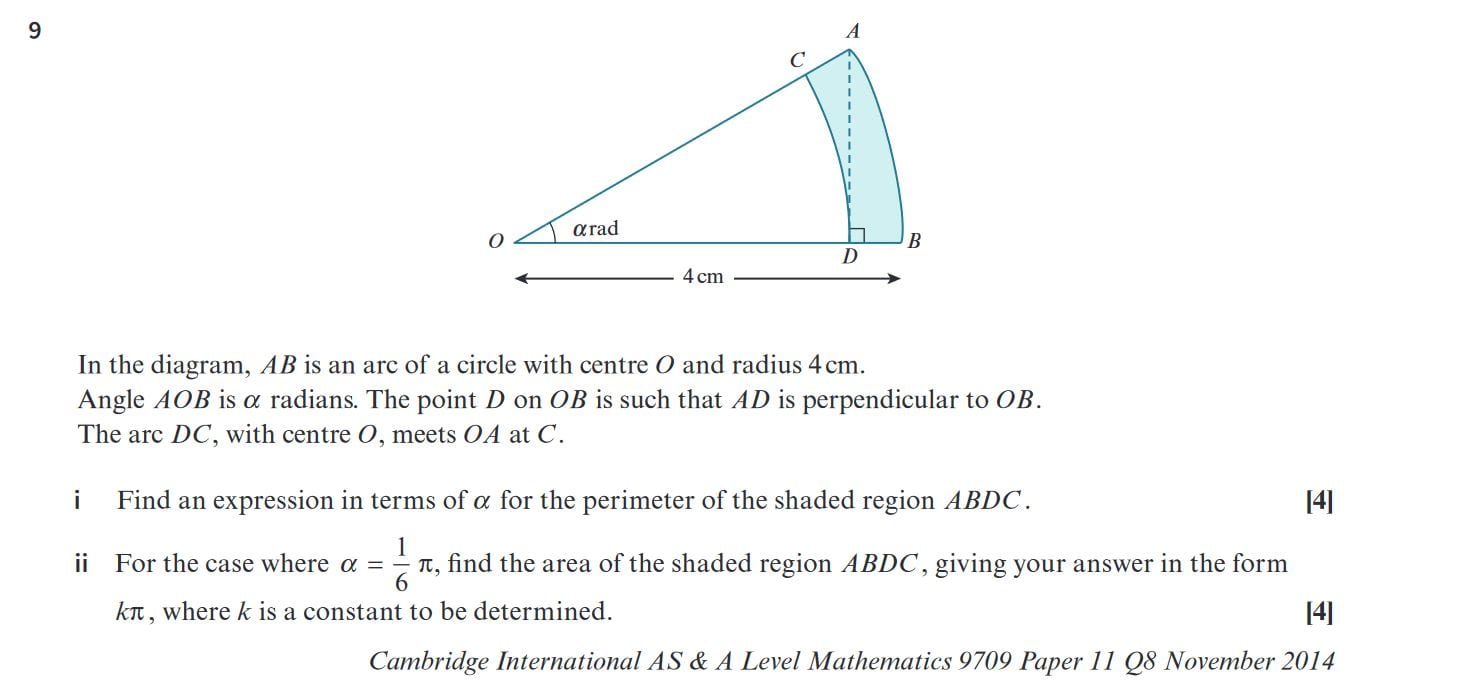
\[ \textbf{2. Find } \alpha \textbf{ and the Perimeter of the Complete Figure:} \] \[ \textbf{i. Finding } \alpha \textbf{ in terms of } \pi \] \[ 1. \text{Area of the sector } OAB: \] \[ \text{The area of a sector is given by } \frac{1}{2}r^2\alpha. \] \[ \text{For } OAB, \text{ the radius } r = 8 \text{ cm and angle } \alpha. \] \[ \text{Area of sector } OAB = \frac{1}{2} \times 8^2 \times \alpha = 32\alpha \text{ cm}^2 \] \[ 2. \text{Area of the semicircle } OAC: \] \[ \text{The semicircle has a radius of } 4 \text{ cm} \text{ (half of } OA). \] \[ \text{Area of the semicircle } OAC = \frac{1}{2} \times \pi \times 4^2 = 8\pi \text{ cm}^2 \] \[ \text{Given that the area of the semicircle is twice the area of the sector } OAB: \] \[ 8\pi = 2 \times 32\alpha \] \[ 8\pi = 64\alpha \] \[ \alpha = \frac{\pi}{8} \] \[ \textbf{ii. Finding the Perimeter of the Complete Figure} \] \[ 1. \text{Perimeter components:} \] \[ \text{The perimeter consists of } OA, \text{ arc } AB, \text{ and the semicircle } AC. \] \[ 2. \text{Length of } OA = 8 \text{ cm}. \] \[ 3. \text{Length of the arc } AB: \] \[ \text{Arc length } = r \alpha = 8 \times \frac{\pi}{8} = \pi \text{ cm} \] \[ 4. \text{Length of the semicircle } AC: \] \[ \text{Circumference of a circle with radius 4 cm is } 2 \pi \times 4 = 8\pi \text{ cm}. \] \[ \text{Length of the semicircle } = \frac{8\pi}{2} = 4\pi \text{ cm} \] \[ 5. \text{Add up all the components:} \] \[ \text{Perimeter} = OA + \text{Arc } AB + \text{Semicircle } AC = 8 + \pi + 4\pi \] \[ = 8 + 5\pi \text{ cm} \] \[ \textbf{i. } \alpha = \frac{\pi}{8} \] \[ \textbf{ii. Perimeter} = 8 + 5\pi \text{ cm} \]


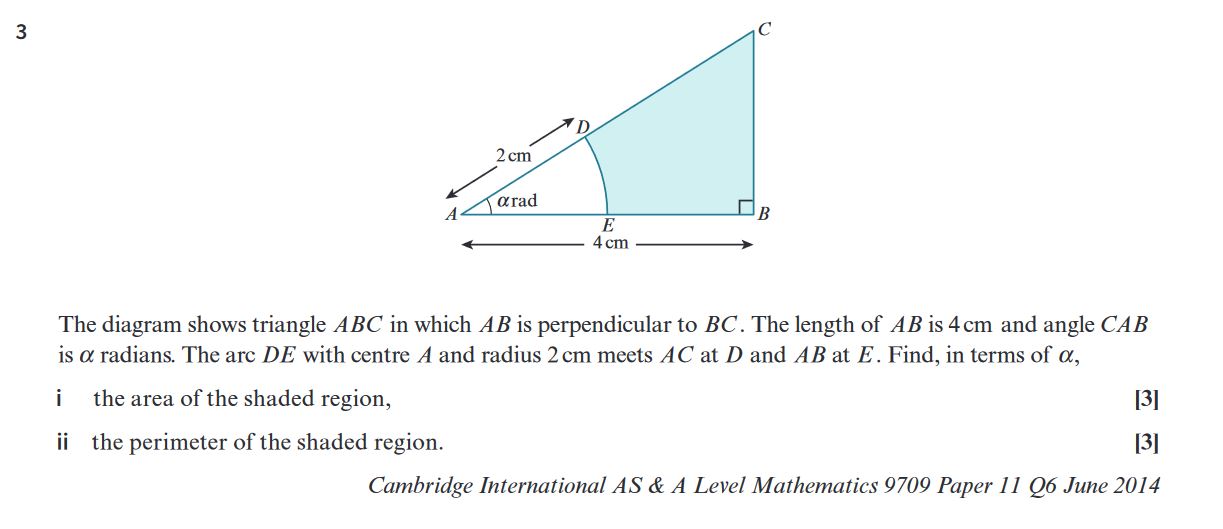
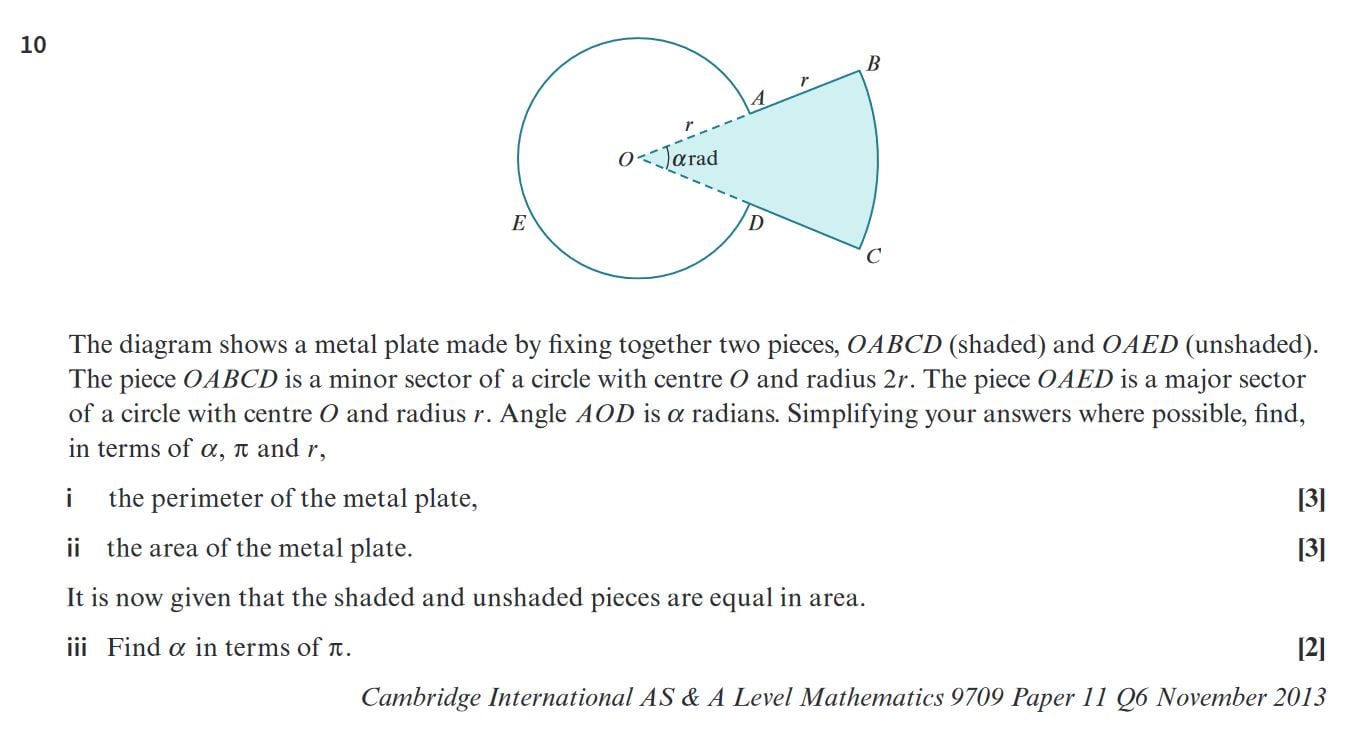
\[ \textbf{3. Finding the Area and Perimeter of the Shaded Region:} \] \[ \textbf{i. Finding the Area of the Shaded Region} \] \[ 1. \text{Area of the sector } ADE: \] \[ \text{The sector } ADE \text{ has a radius of } 2 \text{ cm and angle } \alpha. \] \[ \text{Area of sector } ADE = \frac{1}{2} \times 2^2 \times \alpha = 2\alpha \text{ cm}^2 \] \[ 2. \text{Area of } \triangle ABC: \] \[ \text{Since } AB \text{ is perpendicular to } BC, \triangle ABC \text{ is a right triangle}. \] \[ \text{Base } AB = 4 \text{ cm and height } BC = 2 \text{ cm}. \] \[ \text{Area of } \triangle ABC = \frac{1}{2} \times 4 \times 2 = 4 \text{ cm}^2 \] \[ 3. \text{Subtract the area of the sector from the triangle area:} \] \[ \text{Shaded Area} = 4 - 2\alpha \text{ cm}^2 \] \[ \textbf{i. Area of the Shaded Region} = 4 - 2\alpha \text{ cm}^2 \] \[ \textbf{ii. Finding the Perimeter of the Shaded Region} \] \[ 1. \text{Perimeter components:} \] \[ \text{The perimeter consists of } DE \text{ (arc length), and the line segments } DC \text{ and } CE. \] \[ 2. \text{Length of the arc } DE: \] \[ \text{Arc length} = r \times \alpha = 2 \times \alpha = 2\alpha \text{ cm} \] \[ 3. \text{Length of } DC: \] \[ DC = 2 \text{ cm (height of the triangle)} \] \[ 4. \text{Length of } CE: \] \[ CE = 4 \text{ cm (base of the triangle)} \] \[ 5. \text{Add up all the components:} \] \[ \text{Perimeter} = DE + DC + CE = 2\alpha + 2 + 4 \] \[ = 2\alpha + 6 \text{ cm} \] \[ \textbf{ii. Perimeter of the Shaded Region} = 2\alpha + 6 \text{ cm} \]


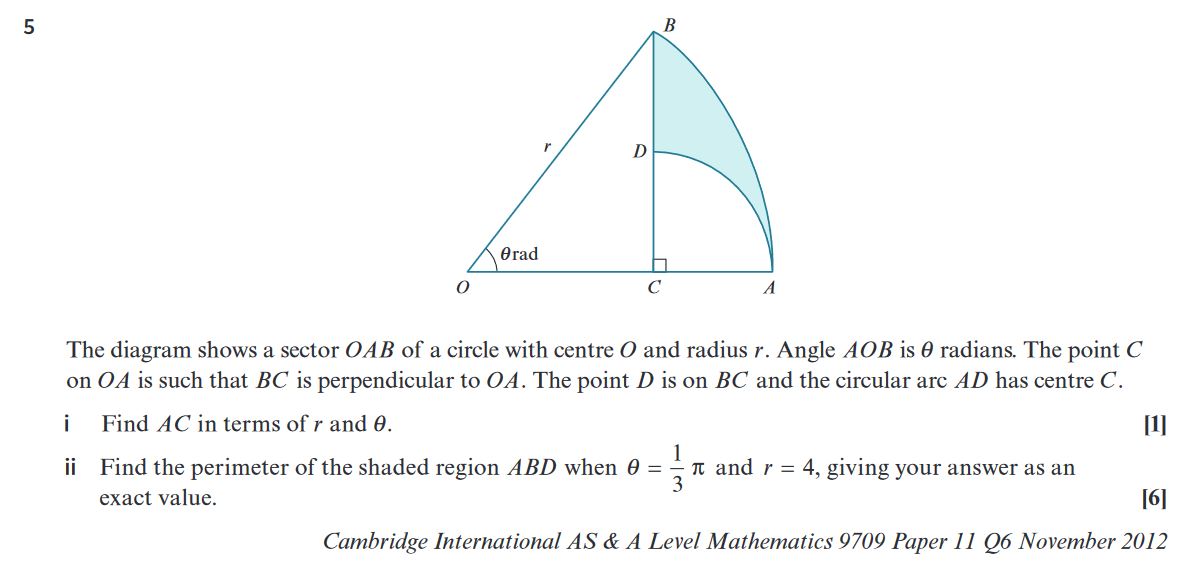
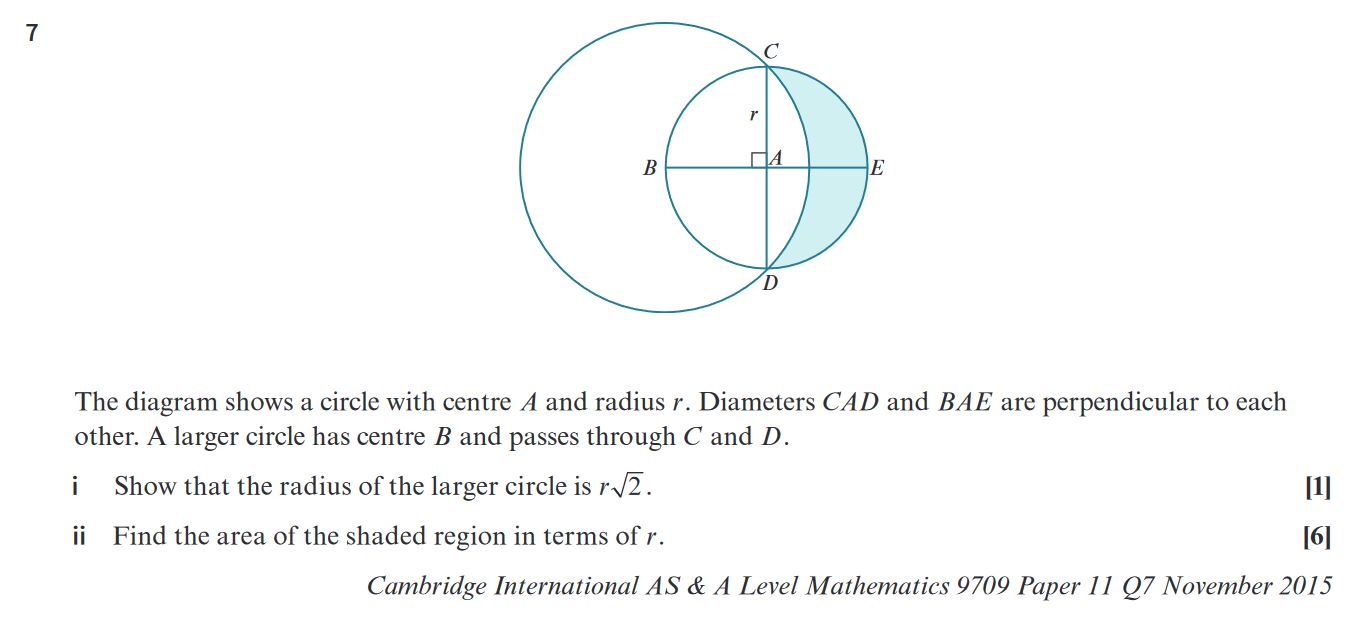
Try these

Try these



Solution

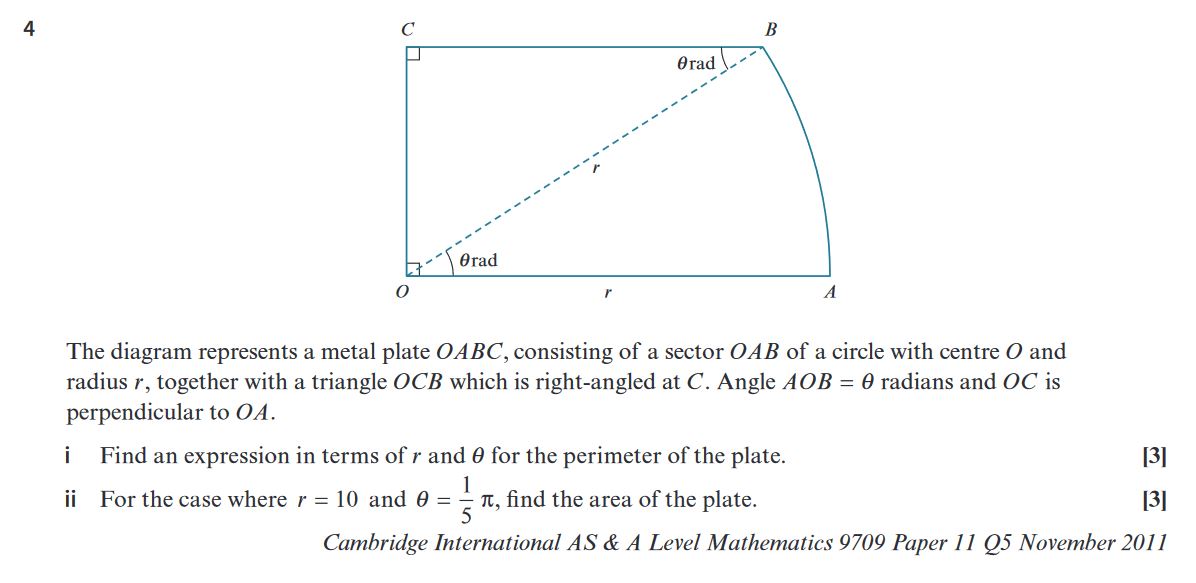
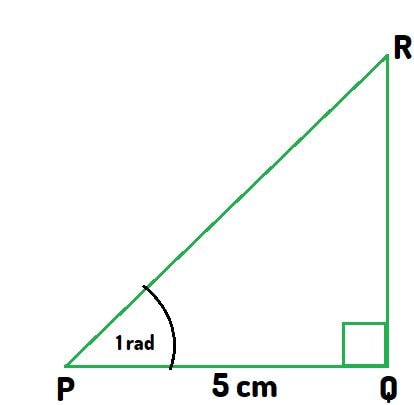
Part (i): Find an expression for the perimeter in terms of \( r \) and \( \theta \).

Arc \( AB \):
The arc length formula is given by:

\[ \text{Arc length } AB = r\theta \]

Line segment \( OA \):
This is a radius of the circle, so:

\[ OA = r \]

Line segment \( OC \):
Since \( OC \) is perpendicular to \( OA \) and forms a right-angled triangle \( OCB \), we use the cosine ratio:

\[ OC = r \cos(\theta) \]

Line segment \( BC \):
Again, using the sine ratio in the right triangle \( OCB \):

\[ BC = r \sin(\theta) \]

Perimeter of the plate:
Thus, the total perimeter \( P \) is the sum of the arc length \( AB \), the line segments \( OA \), \( BC \), and \( OC \):

\[ P = OA + AB + BC + OC \]

Substituting the values:

\[ P = r + r\theta + r \sin(\theta) + r \cos(\theta) \]

Simplifying:

\[ P = r(1 + \theta + \sin(\theta) + \cos(\theta)) \]

Part (ii): Find the area of the plate for \( r = 10 \) and \( \theta = \frac{\pi}{5} \).
The total area consists of two parts:

Area of the sector \( OAB \):
The area of a sector is given by:

\[ A_{\text{sector}} = \frac{1}{2} r^2 \theta \]

Substituting the given values \( r = 10 \) and \( \theta = \frac{\pi}{5} \):

\[ A_{\text{sector}} = \frac{1}{2} (10^2) \left(\frac{\pi}{5}\right) = 50 \times \frac{\pi}{5} = 10 \pi \, \text{cm}^2 \]

Area of the triangle \( OCB \):
The area of a right triangle is given by:

\[ A_{\text{triangle}} = \frac{1}{2} \times OC \times BC \]

Using the expressions for \( OC = r \cos(\theta) \) and \( BC = r \sin(\theta) \), the area becomes:

\[ A_{\text{triangle}} = \frac{1}{2} r^2 \cos(\theta) \sin(\theta) \]

Substituting \( r = 10 \) and \( \theta = \frac{\pi}{5} \):

\[ A_{\text{triangle}} = \frac{1}{2} (10^2) \cos\left(\frac{\pi}{5}\right) \sin\left(\frac{\pi}{5}\right) = 50 \cos\left(\frac{\pi}{5}\right) \sin\left(\frac{\pi}{5}\right) \]

Using values for \( \cos\left(\frac{\pi}{5}\right) = 0.809 \) and \( \sin\left(\frac{\pi}{5}\right) = 0.588 \):

\[ A_{\text{triangle}} = 50 \times 0.809 \times 0.588 = 23.8 \, \text{cm}^2 \]

Total Area:

\[ A_{\text{total}} = A_{\text{sector}} + A_{\text{triangle}} = 10\pi + 23.8 \, \text{cm}^2 \]

Thus, the total area is:

\[ A_{\text{total}} = 10\pi + 23.8 \, \text{cm}^2 \]

Final Rectified Answers:
Perimeter:

\[ P = r(1 + \theta + \sin(\theta) + \cos(\theta)) = 10\left(1 + \frac{\pi}{5} + \sin\left(\frac{\pi}{5}\right) + \cos\left(\frac{\pi}{5}\right)\right) \]

Total Area:

\[ A_{\text{total}} = 10\pi + 23.8 \, \text{cm}^2 \]


Solution \[ \text{In the right-angled triangle } OAC, \text{ we use the cosine function to relate the adjacent side to the hypotenuse:} \] \[ \cos(\theta) = \frac{\text{adjacent side}}{\text{hypotenuse}} \] \[ \text{Here, the adjacent side to the angle } \theta \text{ is } AC, \text{ and the hypotenuse is } OA = r. \] \[ \cos(\theta) = \frac{AC}{r} \] \[ \text{Multiplying both sides by } r, \text{ we get:} \] \[ AC = r \cos(\theta) \] \[ \text{Thus, the length of side } AC \text{ is given by } r \cos(\theta), \text{ which relates the radius of the circle and the angle at } O. \]

Solution \[ \text{Part (i): Show that } A = 12r - r^2. \] \[ \text{Perimeter of the sector } = r\theta + 2r \] \[ r\theta + 2r = 24 \implies r\theta = 24 - 2r \implies \theta = \frac{24 - 2r}{r} \] \[ \text{Area of the sector } A = \frac{1}{2} r^2 \theta = \frac{1}{2} r^2 \times \frac{24 - 2r}{r} = 12r - r^2 \] \[ \text{Part (ii): Express } A \text{ in the form } a - (r - b)^2. \] \[ A = 12r - r^2 = -(r^2 - 12r) \] \[ A = -(r^2 - 12r + 36 - 36) = -(r - 6)^2 + 36 \] \[ \text{Thus, } A = 36 - (r - 6)^2 \text{ where } a = 36 \text{ and } b = 6. \] \[ \text{Part (iii): Find the greatest value of } A \text{ and the corresponding angle.} \] \[ \text{The greatest value of } A = 36 \text{ occurs when } r = 6. \] \[ \text{Find } \theta \text{ using } r = 6: \] \[ 6\theta + 12 = 24 \implies 6\theta = 12 \implies \theta = 2 \text{ radians}. \] \[ \text{Final answer: The greatest value of } A \text{ is } 36, \text{ and the corresponding angle is } 2 \text{ radians}. \]


Solution \[ \text{We are given that the diameters } CAD \text{ and } BAE \text{ are perpendicular to each other.} \] Part i: Show that the radius of the larger circle is \[ r\sqrt{2}\] \[ \text{Using Pythagoras' Theorem in } \triangle ABC: \] \[ BC^2 = AB^2 + AC^2 = r^2 + r^2 = 2r^2 \] \[ BC = \sqrt{2r^2} = r\sqrt{2} \] \[ \text{Hence, the radius of the larger circle is } r\sqrt{2}. \] Part ii: Find the area of the shaded region in terms of } r \[ \text{The area of the smaller circle is: } A_{\text{small}} = \pi r^2 \] \[ \text{The area of the larger circle is: } A_{\text{large}} = 2\pi r^2 \] \[ \text{The area of the quarter circle from the larger circle is: } A_{\text{quarter}} = \frac{\pi r^2}{2} \] \[ \text{The area of the sector in the smaller circle is: } A_{\text{sector}} = \frac{\pi r^2}{4} \] \[ \text{Therefore, the area of the shaded region is: } A_{\text{shaded}} = \frac{\pi r^2}{2} - \frac{\pi r^2}{4} = \frac{\pi r^2}{4} \] \[ \text{Hence, the area of the shaded region is } \frac{\pi r^2}{4}. \]



Solution \[ \text{Part (i): Find the perimeter of the shaded region.} \] The perimeter consists of: 1. Arc \( CB = r\theta \) 2. Segment \( CD = r \sin \theta \) 3. Segment \( DO = r \cos \theta \) Thus, the total perimeter is: \[ P = r(\theta + \sin \theta + \cos \theta) \] \[ \text{Part (ii): Find the area of the shaded region when } r = 5 \text{ cm and } \theta = 0.6. \] 1. The area of sector \( AOB \) is: \[ A_{\text{sector}} = \frac{1}{2}r^2\theta = \frac{1}{2} \times 5^2 \times 0.6 = 7.5 \, \text{cm}^2 \] 2. The area of triangle \( OCD \) is: \[ A_{\text{triangle}} = \frac{1}{2} \times r \cos \theta \times r \sin \theta = \frac{1}{2} \times 5 \times \cos(0.6) \times 5 \times \sin(0.6) \approx 5.82 \, \text{cm}^2 \] 3. The area of the shaded region is: \[ A_{\text{shaded}} = A_{\text{sector}} - A_{\text{triangle}} = 7.5 - 5.82 = 1.68 \, \text{cm}^2 \]



Solution \[ \text{Part (i): Find the perimeter of the shaded region.} \] The perimeter consists of: 1. Arc \( AB = 4\alpha \) 2. Segment \( AD = 4 \sin \alpha \) 3. Arc \( DC = 4 \alpha \) 4. Segment \( OC = 4 \cos \alpha \) Thus, the total perimeter is: \[ \text{Perimeter} = 4\alpha + 4 \sin \alpha + 4\alpha + 4 \cos \alpha = 8\alpha + 4 \sin \alpha + 4 \cos \alpha \] \[ \text{Part (ii): Find the area of the shaded region when } \alpha = \frac{\pi}{6}. \] 1. The area of sector \( AOB \) is: \[ \text{Area of sector} = \frac{1}{2} \times r^2 \times \alpha = \frac{1}{2} \times 4^2 \times \frac{\pi}{6} = \frac{4\pi}{3} \, \text{cm}^2 \] 2. The area of triangle \( AOD \) is: \[ \text{Area of triangle} = \frac{1}{2} \times 4^2 \times \sin \frac{\pi}{6} = 4 \, \text{cm}^2 \] 3. The area of the shaded region is: \[ \text{Shaded area} = \frac{4\pi}{3} - 4 = \frac{4\pi - 12}{3} \, \text{cm}^2 \]



Solution \[ \text{Part (i): Find the perimeter of the metal plate.} \] 1. Arc \( OABC = 2r\alpha \) 2. Arc \( AED = 2\pi r - r\alpha \) 3. Line segments \( OA = OD = r \) Thus, the total perimeter is: \[ \text{Perimeter} = 2r\alpha + (2\pi r - r\alpha) + r + r = r\alpha + 2\pi r + 2r \] \[ \text{Part (ii): Find the area of the metal plate.} \] 1. The area of sector \( OABC \) is: \[ \text{Area of sector OABC} = 2r^2 \alpha \] 2. The area of sector \( OAED \) is: \[ \text{Area of sector OAED} = \pi r^2 - \frac{1}{2} r^2 \alpha \] Thus, the total area is: \[ \text{Total area} = \pi r^2 + \frac{3}{2} r^2 \alpha \] \[ \text{Part (iii): Given that the shaded and unshaded areas are equal, find } \alpha. \] We set the areas equal: \[ 2r^2 \alpha = \pi r^2 - \frac{1}{2} r^2 \alpha \] Solving for \( \alpha \): \[ 5\alpha = 2\pi \quad \Rightarrow \quad \alpha = \frac{2\pi}{5} \]

What is a Radian

Radians

In the diagram above, the magnitude of angle AOB is 1 radian. 1 radian is sometimes written as 1 rad..


Points to Remember




Note

When an angle is written in terms of π, we usually omit the word radian (or rad). Hence, π = 180°


Converting from Degrees to Radian measure

\[ \textbf{Converting from degrees to radians:} \] \[ \text{Since } 180^\circ = \pi, \text{ then } 90^\circ = \frac{\pi}{2}, 45^\circ = \frac{\pi}{4} \text{ etc.} \] \[ \text{We can convert angles that are not simple fractions of } 180^\circ \text{ using the following rule.} \]


Point to Remember


Converting from Radians to Degree measure

\[ \textbf{Converting from radians to degrees:} \] \[ \text{Since } \pi = 180^\circ, \frac{\pi}{6} = 30^\circ, \frac{\pi}{10} = 18^\circ \text{ etc.} \] \[ \text{We can convert angles that are not simple fractions of } \pi \text{ using the following rule.} \]

\[ \text{(It is useful to remember that } 1 \text{ radian} = 1 \times \frac{180}{\pi} \approx 57^\circ\text{.)} \]


Point to Remember




\[ \textbf{Question: Change } 30^\circ \text{ to radians, giving your answer in terms of } \pi. \] \[ \textbf{Question: Change } \frac{5\pi}{9} \text{ radians to degrees.} \]

Method 1

Answer

\[ 180^\circ = \pi \text{ radians} \] \[ \left(\frac{180}{6}\right)^\circ = \frac{\pi}{6} \text{ radians} \] \[ 30^\circ = \frac{\pi}{6} \text{ radians} \]


Method 2

Answer

\[ 30^\circ = \left(30 \times \frac{\pi}{180}\right) \text{ radians} \] \[ 30^\circ = \frac{\pi}{6} \text{ radians} \]

Method 1

Answer

\[ \pi \text{ radians} = 180^\circ \] \[ \frac{\pi}{9} \text{ radians} = 20^\circ \] \[ \frac{5\pi}{9} \text{ radians} = 100^\circ \]

Method 2

Answer

\[ \frac{5\pi}{9} \text{ radians} = \left(\frac{5\pi}{9} \times \frac{180}{\pi}\right)^\circ \] \[ \frac{5\pi}{9} \text{ radians} = 100^\circ \]

Point to Remember: Some important Angles whose Degree - Radian equivalent are given below




\[ \textbf{1. Change these angles to radians, giving your answers in terms of } \pi.\]

\[ \textbf{a. } 20^\circ\] \[ 20^\circ = \left(20 \times \frac{\pi}{180}\right) = \frac{\pi}{9} \text{ radians} \]

\[ \textbf{b. } 40^\circ\] \[ 40^\circ = \left(40 \times \frac{\pi}{180}\right) = \frac{2\pi}{9} \text{ radians} \]

\[ \textbf{c. } 25^\circ\] \[ 25^\circ = \left(25 \times \frac{\pi}{180}\right) = \frac{5\pi}{36} \text{ radians} \]

\[ \textbf{d. } 50^\circ\] \[ 50^\circ = \left(50 \times \frac{\pi}{180}\right) = \frac{5\pi}{18} \text{ radians} \]

\[ \textbf{e. } 5^\circ\] \[ 5^\circ = \left(5 \times \frac{\pi}{180}\right) = \frac{\pi}{36} \text{ radians} \]

\[ \textbf{f. } 150^\circ\] \[ 150^\circ = \left(150 \times \frac{\pi}{180}\right) = \frac{5\pi}{6} \text{ radians} \]

\[ \textbf{g. } 135^\circ\] \[ 135^\circ = \left(135 \times \frac{\pi}{180}\right) = \frac{3\pi}{4} \text{ radians} \]

\[ \textbf{h. } 210^\circ\] \[ 210^\circ = \left(210 \times \frac{\pi}{180}\right) = \frac{7\pi}{6} \text{ radians} \]

\[ \textbf{i. } 225^\circ\] \[ 225^\circ = \left(225 \times \frac{\pi}{180}\right) = \frac{5\pi}{4} \text{ radians} \]

\[ \textbf{j. } 300^\circ\] \[ 300^\circ = \left(300 \times \frac{\pi}{180}\right) = \frac{5\pi}{3} \text{ radians} \]

\[ \textbf{k. } 65^\circ\] \[ 65^\circ = \left(65 \times \frac{\pi}{180}\right) = \frac{13\pi}{36} \text{ radians} \]

\[ \textbf{l. } 540^\circ\] \[ 540^\circ = \left(540 \times \frac{\pi}{180}\right) = 3\pi \text{ radians} \]

\[ \textbf{m. } 9^\circ\] \[ 9^\circ = \left(9 \times \frac{\pi}{180}\right) = \frac{\pi}{20} \text{ radians} \]

\[ \textbf{n. } 35^\circ\] \[ 35^\circ = \left(35 \times \frac{\pi}{180}\right) = \frac{7\pi}{36} \text{ radians} \]

\[ \textbf{o. } 600^\circ\] \[ 600^\circ = \left(600 \times \frac{\pi}{180}\right) = \frac{10\pi}{3} \text{ radians} \]

\[ \textbf{2. Change these angles to degrees.}\]

\[ \textbf{a. } \frac{\pi}{2}\] \[ \frac{\pi}{2} \text{ radians} = \left(\frac{\pi}{2} \times \frac{180}{\pi}\right) = 90^\circ \]

\[ \textbf{b. } \frac{\pi}{3}\] \[ \frac{\pi}{3} \text{ radians} = \left(\frac{\pi}{3} \times \frac{180}{\pi}\right) = 60^\circ \]

\[ \textbf{c. } \frac{\pi}{6}\] \[ \frac{\pi}{6} \text{ radians} = \left(\frac{\pi}{6} \times \frac{180}{\pi}\right) = 30^\circ \]

\[ \textbf{d. } \frac{\pi}{12}\] \[ \frac{\pi}{12} \text{ radians} = \left(\frac{\pi}{12} \times \frac{180}{\pi}\right) = 15^\circ \]

\[ \textbf{e. } \frac{4\pi}{3}\] \[ \frac{4\pi}{3} \text{ radians} = \left(\frac{4\pi}{3} \times \frac{180}{\pi}\right) = 240^\circ \]

\[ \textbf{f. } \frac{4\pi}{9}\] \[ \frac{4\pi}{9} \text{ radians} = \left(\frac{4\pi}{9} \times \frac{180}{\pi}\right) = 80^\circ \]

\[ \textbf{g. } \frac{3\pi}{10}\] \[ \frac{3\pi}{10} \text{ radians} = \left(\frac{3\pi}{10} \times \frac{180}{\pi}\right) = 54^\circ \]

\[ \textbf{h. } \frac{7\pi}{12}\] \[ \frac{7\pi}{12} \text{ radians} = \left(\frac{7\pi}{12} \times \frac{180}{\pi}\right) = 105^\circ \]

\[ \textbf{i. } \frac{9\pi}{20}\] \[ \frac{9\pi}{20} \text{ radians} = \left(\frac{9\pi}{20} \times \frac{180}{\pi}\right) = 81^\circ \]

\[ \textbf{j. } \frac{9\pi}{2}\] \[ \frac{9\pi}{2} \text{ radians} = \left(\frac{9\pi}{2} \times \frac{180}{\pi}\right) = 810^\circ \]

\[ \textbf{k. } \frac{7\pi}{5}\] \[ \frac{7\pi}{5} \text{ radians} = \left(\frac{7\pi}{5} \times \frac{180}{\pi}\right) = 252^\circ \]

\[ \textbf{l. } \frac{4\pi}{15}\] \[ \frac{4\pi}{15} \text{ radians} = \left(\frac{4\pi}{15} \times \frac{180}{\pi}\right) = 48^\circ \]

\[ \textbf{m. } \frac{5\pi}{4}\] \[ \frac{5\pi}{4} \text{ radians} = \left(\frac{5\pi}{4} \times \frac{180}{\pi}\right) = 225^\circ \]

\[ \textbf{n. } \frac{7\pi}{3}\] \[ \frac{7\pi}{3} \text{ radians} = \left(\frac{7\pi}{3} \times \frac{180}{\pi}\right) = 420^\circ \]

\[ \textbf{o. } \frac{9\pi}{8}\] \[ \frac{9\pi}{8} \text{ radians} = \left(\frac{9\pi}{8} \times \frac{180}{\pi}\right) = 202.5^\circ \]


Write each of these angles in radians, correct to 3 significant figures.

\[ \textbf{a. } 28^\circ \] \[ 28^\circ = \left(28 \times \frac{\pi}{180}\right) = 0.489 \text{ radians (3 significant figures)} \]

\[ \textbf{b. } 32^\circ \] \[ 32^\circ = \left(32 \times \frac{\pi}{180}\right) = 0.559 \text{ radians (3 significant figures)} \]

\[ \textbf{c. } 47^\circ\] \[ 47^\circ = \left(47 \times \frac{\pi}{180}\right) = 0.820 \text{ radians (3 significant figures)} \]

\[ \textbf{d. } 200^\circ\] \[ 200^\circ = \left(200 \times \frac{\pi}{180}\right) = 3.49 \text{ radians (3 significant figures)} \]

\[ \textbf{e. } 320^\circ\] \[ 320^\circ = \left(320 \times \frac{\pi}{180}\right) = 5.59 \text{ radians (3 significant figures)} \]

Write each of these angles in degrees, correct to 1 decimal place.

\[ \textbf{a. } 1.2 \text{ rad}\] \[ 1.2 \text{ rad} = \left(1.2 \times \frac{180}{\pi}\right) = 68.8^\circ \text{ (1 decimal place)} \]

\[ \textbf{b. } 0.8 \text{ rad}\] \[ 0.8 \text{ rad} = \left(0.8 \times \frac{180}{\pi}\right) = 45.8^\circ \text{ (1 decimal place)} \]

\[ \textbf{c. } 1.34 \text{ rad}\] \[ 1.34 \text{ rad} = \left(1.34 \times \frac{180}{\pi}\right) = 76.8^\circ \text{ (1 decimal place)} \]

\[ \textbf{d. } 1.52 \text{ rad}\] \[ 1.52 \text{ rad} = \left(1.52 \times \frac{180}{\pi}\right) = 87.1^\circ \text{ (1 decimal place)} \]

\[ \textbf{e. } 0.79 \text{ rad}\] \[ 0.79 \text{ rad} = \left(0.79 \times \frac{180}{\pi}\right) = 45.3^\circ \text{ (1 decimal place)} \]


Question

Calculate the length of QR

Solution:

Given: \( \angle PQR = 1 \text{ radian} \) and \( PQ = 5 \text{ cm} \). We need to find the length of \( QR \).

To find \( QR \) in a right triangle, we use the tangent function since we know the angle and the adjacent side:

\[ \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} = \frac{QR}{PQ} \] Substituting the given values: \[ \tan(1 \text{ rad}) = \frac{QR}{5 \text{ cm}} \] Solving for \( QR \): \[ QR = 5 \text{ cm} \times \tan(1 \text{ rad}) \] The value of \( \tan(1 \text{ rad}) \approx 1.5574 \). Therefore: \[ QR = 5 \times 1.5574 \approx 7.787 \text{ cm} \]

Thus, the correct length of \( QR \) is approximately \( 7.787 \) cm.


Question

Robert is told the size of angle BAC in degrees and he is then asked to calculate the length of the line BC. He uses his calculator but forgets that his calculator is in radian mode. Luckily he still manages to obtain the correct answer. Given that angle BAC is between 10° and 15° , use graphing software to help you find the size of angle BAC, correct to 2 decimal places.

\[ \text{Given: } AC = 6 \text{ cm}, \text{ and } \angle BAC \text{ is between } 10^\circ \text{ and } 15^\circ. \] \[ \text{Robert uses his calculator in radian mode to calculate } BC. \] \[ BC = AC \times \sin(\angle BAC) \text{ in radians}. \]

\[ \textbf{Step 1: Convert degrees to radians for the given range.} \] \[ 10^\circ = \frac{10 \times \pi}{180} = 0.1745 \text{ radians (approx)} \] \[ 15^\circ = \frac{15 \times \pi}{180} = 0.2618 \text{ radians (approx)} \]

\[ \textbf{Step 2: Use graphing software to find } \angle BAC \textbf{ within the given range.} \]

We set up the equation: \[ BC = 6 \text{ cm} \times \sin(\angle BAC) \] Since Robert gets the correct answer, we test different values within the radian range (0.1745 to 0.2618). Let’s find the angle that matches the calculated value of \( BC \).

\[ \textbf{Step 3: Find the correct value using the sine function.}\] Assume \( \angle BAC = 0.2094 \) radians (which is \( 12^\circ \) approximately): \[ BC = 6 \times \sin(0.2094) \approx 6 \times 0.2079 = 1.247 \text{ cm} \]

\[ \textbf{Step 4: Convert the angle back to degrees and round to 2 decimal places.}\] \[ \angle BAC = 0.2094 \times \frac{180}{\pi} = 12.00^\circ \text{ (correct to 2 decimal places)} \]

\[ \textbf{Final Answer:} \textbf{The size of angle} \angle BAC = 12.00^\circ \]

Worksheet

\[ \textbf{Problem Set} \]

\[ \textbf{1. Convert the following angles to radians, giving your answers in terms of } \pi: \] \[ \textbf{a. } 15^\circ \] \[ \textbf{b. } 75^\circ \] \[ \textbf{c. } 120^\circ \] \[ \textbf{d. } 210^\circ \] \[ \textbf{e. } 330^\circ \]

\[ \textbf{2. Convert the following angles to degrees:} \] \[ \textbf{a. } \frac{\pi}{8} \] \[ \textbf{b. } \frac{2\pi}{3} \] \[ \textbf{c. } \frac{5\pi}{12} \] \[ \textbf{d. } \frac{7\pi}{4} \] \[ \textbf{e. } \frac{11\pi}{6} \]

\[ \textbf{3. Write each of these angles in radians, correct to 3 significant figures:} \] \[ \textbf{a. } 35^\circ \] \[ \textbf{b. } 150^\circ \] \[ \textbf{c. } 240^\circ \] \[ \textbf{d. } 75^\circ \] \[ \textbf{e. } 10^\circ \]

\[ \textbf{4. Write each of these angles in degrees, correct to 1 decimal place:} \] \[ \textbf{a. } 0.95 \text{ rad} \] \[ \textbf{b. } 1.8 \text{ rad} \] \[ \textbf{c. } 2.4 \text{ rad} \] \[ \textbf{d. } 0.5 \text{ rad} \] \[ \textbf{e. } 3.2 \text{ rad} \]

\[ \textbf{5.} \text{ A triangle has an angle of } 1.5 \text{ rad and a side length of } 7 \text{ cm}. \text{ Find the length of the opposite side to this angle.} \]

\[ \textbf{6.} \text{ In a right triangle, angle } \theta = 0.75 \text{ rad and the hypotenuse is } 10 \text{ cm}. \text{ Calculate the length of the adjacent side.} \]

\[ \textbf{7.} \text{ A sector has a central angle of } 2 \text{ rad and a radius of } 8 \text{ cm}. \text{ Find the arc length of the sector.} \]

\[ \textbf{8.} \text{ Robert measures angle } BAC \text{ as } 18^\circ \text{ but accidentally uses his calculator in radian mode when computing the length of side } BC. \] \[\text{ Given that } AC = 5 \text{ cm}, \text{ find the length of } BC \text{ using the radian mode calculation.} \]

\[ \textbf{Answer Key} \]

\[ \textbf{1. Convert to radians:} \] \[ \textbf{a. } 15^\circ = \frac{\pi}{12} \] \[ \textbf{b. } 75^\circ = \frac{5\pi}{12} \] \[ \textbf{c. } 120^\circ = \frac{2\pi}{3} \] \[ \textbf{d. } 210^\circ = \frac{7\pi}{6} \] \[ \textbf{e. } 330^\circ = \frac{11\pi}{6} \]

\[ \textbf{2. Convert to degrees:} \] \[ \textbf{a. } \frac{\pi}{8} = 22.5^\circ \] \[ \textbf{b. } \frac{2\pi}{3} = 120^\circ \] \[ \textbf{c. } \frac{5\pi}{12} = 75^\circ \] \[ \textbf{d. } \frac{7\pi}{4} = 315^\circ \] \[ \textbf{e. } \frac{11\pi}{6} = 330^\circ \]

\[ \textbf{3. Write in radians:} \] \[ \textbf{a. } 35^\circ = 0.611 \text{ radians} \] \[ \textbf{b. } 150^\circ = 2.62 \text{ radians} \] \[ \textbf{c. } 240^\circ = 4.19 \text{ radians} \] \[ \textbf{d. } 75^\circ = 1.31 \text{ radians} \] \[ \textbf{e. } 10^\circ = 0.175 \text{ radians} \]

\[ \textbf{4. Write in degrees:} \] \[ \textbf{a. } 0.95 \text{ rad} = 54.4^\circ \] \[ \textbf{b. } 1.8 \text{ rad} = 103.1^\circ \] \[ \textbf{c. } 2.4 \text{ rad} = 137.5^\circ \] \[ \textbf{d. } 0.5 \text{ rad} = 28.6^\circ \] \[ \textbf{e. } 3.2 \text{ rad} = 183.4^\circ \]

\[ \textbf{5. Solution:} \] \[ \text{Opposite side} = 7 \times \sin(1.5) = 7 \times 0.997 = 6.98 \text{ cm} \]

\[ \textbf{6. Solution:} \] \[ \text{Adjacent side} = 10 \times \cos(0.75) = 10 \times 0.731 = 7.31 \text{ cm} \]

\[ \textbf{7. Solution:} \] \[ \text{Arc length} = 2 \times 8 = 16 \text{ cm} \]

\[ \textbf{8. Solution:} \] \[ BC = 5 \times \sin(0.314) = 5 \times 0.309 = 1.55 \text{ cm} \]

© 2024 Pure Mathematics I AS Level Complete Guide