Coordinate Geometry-Vocabulary List

Coordinate Geometry Vocabulary

Cartesian Plane: A plane defined by two perpendicular number lines, called the x-axis and y-axis, intersecting at a point called the origin.
Origin: The point where the x-axis and y-axis intersect, represented as $(0, 0)$ .
Quadrants: The four regions of the Cartesian plane, divided by the x-axis and y-axis. They are labeled as Quadrant I, II, III, and IV.
Coordinates: An ordered pair of numbers $(x, y)$ used to locate a point on the Cartesian plane, where $x$ is the horizontal position (x-coordinate) and $y$ is the vertical position (y-coordinate).
Distance Formula: A formula used to find the distance between two points $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ on the Cartesian plane:
$d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$
Midpoint Formula: A formula used to find the midpoint of a line segment connecting two points $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ :
$(\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$
Slope: A measure of the steepness or incline of a line, defined as the ratio of the vertical change to the horizontal change between two points on the line:
$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$
Slope-Intercept Form: The equation of a line written as $y = m x + c$ , where $m$ is the slope and $c$ is the y-intercept (the point where the line crosses the y-axis).
Point-Slope Form: The equation of a line that passes through a point $(x_{1}, y_{1})$ with slope $m$ :
$y - y_{1} = m (x - x_{1})$
Y-Intercept: The point where a line crosses the y-axis, represented as $(0, y)$ .
X-Intercept: The point where a line crosses the x-axis, represented as $(x, 0)$ .
Equation of a Circle: The equation of a circle with center $(a, b)$ and radius $r$ is:
$(x - a)^{2} + (y - b)^{2} = r^{2}$
Collinear Points: Points that lie on the same straight line.
Parallel Lines: Lines in the same plane that never intersect, having the same slope but different y-intercepts.
Perpendicular Lines: Lines that intersect at a right angle (90°). The slopes of perpendicular lines are negative reciprocals of each other:
$m_{1} \times m_{2} = - 1$
Isosceles Triangle: A triangle with two equal sides. In coordinate geometry, the distance formula can be used to check whether two sides of a triangle are equal.
Equilateral Triangle: A triangle where all three sides are of equal length. Again, the distance formula is used to verify this.
Right-Angled Triangle: A triangle with one angle equal to 90°. The Pythagorean theorem is often used to verify right-angled triangles:
$c^{2} = a^{2} + b^{2}$
Collinearity Test: A method of determining if three points are collinear by calculating the slopes of the line segments between them. If the slopes are equal, the points are collinear.
Distance between Parallel Lines: The shortest distance between two parallel lines is given by:
$d = \frac{| c_{1} - c_{2} |}{\sqrt{a^{2} + b^{2}}}$
Where $c_{1}$ and $c_{2}$ are the constants in the equations of the lines, and $a$ and $b$ are coefficients of $x$ and $y$ in the general line equation.
Centroid: The point where the medians of a triangle intersect, calculated as the average of the x-coordinates and y-coordinates of the triangle's vertices:
$G = (\frac{x_{1} + x_{2} + x_{3}}{3}, \frac{y_{1} + y_{2} + y_{3}}{3})$
Pythagorean Theorem: A fundamental relation in a right-angled triangle between the lengths of the hypotenuse and the other two sides:
$c^{2} = a^{2} + b^{2}$
Inclination of a Line: The angle that a line makes with the positive x-axis, usually denoted by $θ$ . The slope $m$ of the line is related to the inclination angle by:
$m = \tan (θ)$
General Form of a Line: The equation of a line in the form:
$a x + b y + c = 0$
where $a$ , $b$ , and $c$ are constants.
Vector Equation of a Line: The vector form of the equation of a line can be written as:
$\vec{r} = \vec{r_{0}} + t \vec{d}$
where $\vec{r_{0}}$ is a point on the line, $\vec{d}$ is the direction vector, and $t$ is a scalar.
Area of a Triangle (using coordinates): The area of a triangle with vertices $(x_{1}, y_{1})$ , $(x_{2}, y_{2})$ , and $(x_{3}, y_{3})$ can be calculated using the formula:
$Area = \frac{1}{2} | x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2}) |$
Centroid of a Triangle: The point where the three medians of a triangle intersect. The centroid divides each median into a 2:1 ratio, with the longer part closer to the vertex.
Circumcenter: The point where the perpendicular bisectors of the sides of a triangle intersect. It is the center of the circumcircle, the circle that passes through all three vertices of the triangle.
Orthocenter: The point where the altitudes of a triangle intersect. The altitude is the perpendicular segment from a vertex to the opposite side.

Straight Lines

Finding the Equation of a Straight Line

The equation of a line can be written in various forms. The slope-intercept form is:

$y = m x + c$

Where:

$m$ is the slope.
$c$ is the y-intercept.

The point-slope form is:

$y - y_{1} = m (x - x_{1})$

$m$ is the slope.
$(x_{1}, y_{1})$ is a point on the line.

Midpoint formula

Midpoint Formula:

$M = (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$

Distance Formula:

$P Q = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$

Solved Problem

The point $M (\frac{5}{2}, - 7)$ is the midpoint of the line segment joining the points $P (- 3, 6)$ and $Q (a, b)$ .

Find the value of $a$ and $b$ .

Solution:

We use the midpoint formula:

$M = (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$

Given that the midpoint is $M (\frac{5}{2}, - 7)$ , and the points are $P (- 3, 6)$ and $Q (a, b)$ , we substitute into the formula:

$(\frac{- 3 + a}{2}, \frac{6 + b}{2}) = (\frac{5}{2}, - 7)$

Step 1: Equating the x-coordinates

Equate the x-coordinates:

$\frac{- 3 + a}{2} = \frac{5}{2}$

Multiplying both sides by 2:

$- 3 + a = 5$

Solve for $a$ :

$a = 5 + 3 = 8$

Step 2: Equating the y-coordinates

Equate the y-coordinates:

$\frac{6 + b}{2} = - 7$

Multiplying both sides by 2:

$6 + b = - 14$

Solve for $b$ :

$b = - 14 - 6 = - 20$

Final Answer:

The values are:

$a = 8 and b = - 20$

Example :

Parallelogram Question

Three of the vertices of a parallelogram, $A B C D$ , are $A (- 6, 2)$ , $B (0, - 3)$ , and $C (5, 1)$ .

a) Find the midpoint of $A C$ .
b) Find the coordinates of $D$ .

Solution:

Step 1: Find the midpoint of $A C$

The formula for the midpoint between two points $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ is:

$Midpoint = (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$

Substitute $A (- 6, 2)$ and $C (5, 1)$ :

$Midpoint of A C = (\frac{- 6 + 5}{2}, \frac{2 + 1}{2}) = (\frac{- 1}{2}, \frac{3}{2})$

Step 2: Find the coordinates of $D$

Let the coordinates of $D$ be $(m, n)$ . Since $A B C D$ is a parallelogram, the midpoint of $B D$ is the same as the midpoint of $A C$ .

The midpoint of $B D$ is:

$(\frac{0 + m}{2}, \frac{- 3 + n}{2})$

Equating with the midpoint of $A C$ , we get the following system of equations:

$\frac{0 + m}{2} = \frac{- 1}{2} and \frac{- 3 + n}{2} = \frac{3}{2}$

Step 3: Solve for $m$ and $n$

For the x-coordinates:

$\frac{0 + m}{2} = \frac{- 1}{2}$

Multiply both sides by 2:

$m = - 1$

For the y-coordinates:

$\frac{- 3 + n}{2} = \frac{3}{2}$

Multiply both sides by 2:

$- 3 + n = 3$

Solve for $n$ :

$n = 6$

Final Answer:

The midpoint of $A C$ is $(\frac{- 1}{2}, \frac{3}{2})$ .
The coordinates of $D$ are $(- 1, 6)$ .

Example :

Distance Formula Problem

The distance between two points $P (- 4, a)$ and $Q (a - 3, - 5)$ is 20.

Find the two possible values of $a$ .

Solution:

Step 1: Apply the distance formula

The distance formula is:

$d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$

Substituting the coordinates $P (- 4, a)$ and $Q (a - 3, - 5)$ into the formula:

$20 = \sqrt{((a - 3) - (- 4))^{2} + (- 5 - a)^{2}}$

Simplify:

$20 = \sqrt{(a - 3 + 4)^{2} + (- 5 - a)^{2}}$

$20 = \sqrt{(a + 1)^{2} + (- 5 - a)^{2}}$

Step 2: Square both sides

Square both sides to remove the square root:

$20^{2} = (a + 1)^{2} + (- 5 - a)^{2}$

$400 = (a + 1)^{2} + (- 5 - a)^{2}$

Step 3: Expand both terms

Expand both squares:

$400 = (a^{2} + 2 a + 1) + (a^{2} + 10 a + 25)$

Step 4: Combine like terms

Combine the terms:

$400 = 2 a^{2} + 12 a + 26$

Step 5: Rearrange the equation

Rearrange the terms to form a quadratic equation:

$0 = 2 a^{2} + 12 a + 26 - 400$

$0 = 2 a^{2} + 12 a - 374$

Divide by 2:

$0 = a^{2} + 6 a - 187$

Step 6: Solve the quadratic equation

Use the quadratic formula:

$a = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

Substitute $b = 6$ , $a = 1$ , and $c = - 187$ :

$a = \frac{- 6 \pm \sqrt{6^{2} - 4 (1) (- 187)}}{2 (1)}$

$a = \frac{- 6 \pm \sqrt{36 + 748}}{2}$

$a = \frac{- 6 \pm \sqrt{784}}{2}$

$a = \frac{- 6 \pm 28}{2}$

Step 7: Calculate the two possible values of $a$

The two values are:

$a = \frac{- 6 + 28}{2} = \frac{22}{2} = 11$

$a = \frac{- 6 - 28}{2} = \frac{- 34}{2} = - 17$

Final Answer:

The two possible values of $a$ are $11$ and $- 17$ .

Text Book Solutions

Step-by-Step Solutions for 5 Geometry Questions

Question 1a:

Calculate the lengths of the sides of the triangle $P Q R$ .

Points: $P (- 4, 6)$ , $Q (6, 1)$ , $R (2, 9)$

Step 1: Calculate $P Q$

Using the distance formula:

$P Q = \sqrt{(6 - (- 4))^{2} + (1 - 6)^{2}} = 5 \sqrt{5}$

Step 2: Calculate $Q R$

$Q R = \sqrt{(2 - 6)^{2} + (9 - 1)^{2}} = 4 \sqrt{5}$

Step 3: Calculate $P R$

$P R = \sqrt{(2 - (- 4))^{2} + (9 - 6)^{2}} = 3 \sqrt{5}$

Step 4: Verify if the triangle is right-angled

Check Pythagoras:

$P Q^{2} = P R^{2} + Q R^{2}$

$(5 \sqrt{5})^{2} = (3 \sqrt{5})^{2} + (4 \sqrt{5})^{2}$

$125 = 45 + 80 = 125$

The triangle is right-angled.

Question 1b:

Calculate the lengths of the sides of the triangle $P Q R$ .

Points: $P (- 5, 2)$ , $Q (9, 3)$ , $R (- 2, 8)$

Step 1: Calculate $P Q$

$P Q = \sqrt{(9 - (- 5))^{2} + (3 - 2)^{2}} = \sqrt{197}$

Step 2: Calculate $Q R$

$Q R = \sqrt{(- 2 - 9)^{2} + (8 - 3)^{2}} = \sqrt{146}$

Step 3: Calculate $P R$

$P R = \sqrt{(- 2 - (- 5))^{2} + (8 - 2)^{2}} = 3 \sqrt{5}$

Step 4: Conclusion

Since $P Q^{2} \neq P R^{2} + Q R^{2}$ , the triangle is not right-angled.

Question 2:

Show that triangle $P Q R$ is a right-angled isosceles triangle and calculate the area.

Points: $P (1, 6)$ , $Q (- 2, 1)$ , $R (3, - 2)$

Step 1: Calculate side lengths

$P Q$ :

$P Q = \sqrt{((- 2) - 1)^{2} + (1 - 6)^{2}} = \sqrt{34}$

$P R$ :

$P R = \sqrt{(3 - 1)^{2} + (- 2 - 6)^{2}} = \sqrt{68}$

$Q R$ :

$Q R = \sqrt{(3 - (- 2))^{2} + (- 2 - 1)^{2}} = \sqrt{34}$

Step 2: Verify right-angle

Pythagoras holds:

$P R^{2} = P Q^{2} + Q R^{2}$

$68 = 34 + 34$

Step 3: Calculate the area

The area of a right-angled isosceles triangle is:

$Area = \frac{1}{2} \times P Q \times Q R = 17$

Question 3:

The distance between two points, $P (a, - 1)$ and $Q (- 5, a)$ , is $4 \sqrt{5}$ . Find the two possible values of $a$ .

Step 1: Use the distance formula

$4 \sqrt{5} = \sqrt{(- 5 - a)^{2} + (a + 1)^{2}}$

Square both sides:

$80 = (25 + 10 a + a^{2}) + (a^{2} + 2 a + 1)$

Step 2: Simplify the equation

$80 = 2 a^{2} + 12 a + 26$

Rearrange:

$2 a^{2} + 12 a - 54 = 0$

Divide by 2:

$a^{2} + 6 a - 27 = 0$

Step 3: Solve using the quadratic formula

$a = \frac{- 6 \pm \sqrt{6^{2} - 4 (1) (- 27)}}{2 (1)}$

$a = \frac{- 6 \pm \sqrt{144}}{2}$

Two possible values of $a$ :

$a = 3 or a = - 9$

Question 4:

The distance between two points, $P (- 3, - 2)$ and $Q (b, 2 b)$ , is 10. Find the two possible values of $b$ .

Step 1: Use the distance formula

$10 = \sqrt{(b - (- 3))^{2} + (2 b - (- 2))^{2}}$

Square both sides:

$100 = (b + 3)^{2} + (2 b + 2)^{2}$

Step 2: Expand the terms

$100 = (b^{2} + 6 b + 9) + (4 b^{2} + 8 b + 4)$

Combine terms:

$100 = 5 b^{2} + 14 b + 13$

Step 3: Solve the quadratic equation

$b = \frac{- 14 \pm \sqrt{14^{2} - 4 (5) (- 87)}}{2 (5)}$

$b = \frac{- 14 \pm \sqrt{1936}}{10}$

Two possible values of $b$ :

$b = 3 or b = - 5.8$

Question 5:

The point $(- 2, - 3)$ is the midpoint of the line segment joining $P (- 6, - 5)$ and $Q (a, b)$ . Find the values of $a$ and $b$ .

Step 1: Use the midpoint formula

Midpoint formula:

$(\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$

Substitute $P (- 6, - 5)$ , $Q (a, b)$ , and the midpoint $(- 2, - 3)$ :

$(\frac{- 6 + a}{2}, \frac{- 5 + b}{2}) = (- 2, - 3)$

Step 2: Solve for $a$

Equating x-coordinates:

$\frac{- 6 + a}{2} = - 2$

Multiply both sides by 2:

$- 6 + a = - 4$

$a = 2$

Step 3: Solve for $b$

Equating y-coordinates:

$\frac{- 5 + b}{2} = - 3$

Multiply both sides by 2:

$- 5 + b = - 6$

$b = - 1$

Final Answer:

Values of $a$ and $b$ are $2$ and $- 1$ , respectively.

Geometry Worksheet

Instructions:

Solve the following problems. Show all your work and justify your answers.

Question 1:

Calculate the lengths of the sides of triangle $P Q R$ . Use your answers to determine whether the triangle is right-angled.

Points: $P (- 3, 5)$ , $Q (4, 1)$ , $R (0, 7)$

Question 2:

The distance between two points $P (a, - 2)$ and $Q (- 6, a)$ is $5 \sqrt{5}$ . Find the two possible values of $a$ .

Question 3:

Show that the triangle with vertices $P (1, 1)$ , $Q (- 2, 1)$ , and $R (1, - 2)$ is an isosceles right-angled triangle. Calculate the area of the triangle.

Question 4:

The point $(- 1, 3)$ is the midpoint of the line segment joining $P (- 5, - 1)$ and $Q (a, b)$ . Find the values of $a$ and $b$ .

Question 5:

The distance between two points $P (3, - 4)$ and $Q (b, 2 b)$ is 13. Find the two possible values of $b$ .

Question 6:

Find the length of the diagonal of a rectangle whose vertices are $P (1, 2)$ , $Q (7, 2)$ , $R (7, - 6)$ , and $S (1, - 6)$ .

Question 7:

Determine whether the points $A (- 2, - 3)$ , $B (3, 2)$ , and $C (6, 5)$ are collinear.

Question 8:

The distance between two points $P (1, 1)$ and $Q (4, a)$ is 5. Find the two possible values of $a$ .

Question 9:

Find the area of triangle $P Q R$ with vertices $P (0, 0)$ , $Q (6, 0)$ , and $R (6, 8)$ .

Question 10:

The point $(- 4, - 1)$ is the midpoint of the line segment joining $P (2, 7)$ and $Q (a, b)$ . Find the values of $a$ and $b$ .

Answer Key

Answer 1:

Using the distance formula:

$P Q = \sqrt{(4 - (- 3))^{2} + (1 - 5)^{2}} = \sqrt{7^{2} + (- 4)^{2}} = \sqrt{49 + 16} = \sqrt{65}$

$Q R = \sqrt{(0 - 4)^{2} + (7 - 1)^{2}} = \sqrt{(- 4)^{2} + 6^{2}} = \sqrt{16 + 36} = \sqrt{52}$

$P R = \sqrt{(0 - (- 3))^{2} + (7 - 5)^{2}} = \sqrt{3^{2} + 2^{2}} = \sqrt{9 + 4} = \sqrt{13}$

Since $P Q^{2} \neq P R^{2} + Q R^{2}$ , the triangle is not right-angled.

Answer 2:

Using the distance formula:

$5 \sqrt{5} = \sqrt{(- 6 - a)^{2} + (a + 2)^{2}}$

Square both sides and simplify:

$125 = (a + 6)^{2} + (a + 2)^{2}$

Solve the resulting quadratic to find $a = 5$ and $a = - 1$ .

Answer 3:

Check side lengths:

$P Q = \sqrt{(1 - (- 2))^{2} + (1 - 1)^{2}} = \sqrt{3^{2} + 0^{2}} = 3$

$P R = \sqrt{(1 - 1)^{2} + (1 - (- 2))^{2}} = \sqrt{0^{2} + 3^{2}} = 3$

Since $P Q = P R$ and the Pythagorean theorem holds, the triangle is right-angled isosceles.

Area of triangle:

$Area = \frac{1}{2} \times 3 \times 3 = 4.5 square units$

Answer 4:

Using the midpoint formula:

$(- 1, 3) = (\frac{- 5 + a}{2}, \frac{- 1 + b}{2})$

Solving, we get $a = 3$ and $b = 7$ .

Answer 5:

Using the distance formula:

$13 = \sqrt{(b - 3)^{2} + (2 b - (- 4))^{2}}$

Solve to find $b = 3$ or $b = - 1$ .

Answer 6:

The diagonal of the rectangle is the distance between $P (1, 2)$ and $R (7, - 6)$ :

$P R = \sqrt{(7 - 1)^{2} + (- 6 - 2)^{2}} = \sqrt{6^{2} + (- 8)^{2}} = \sqrt{36 + 64} = \sqrt{100} = 10$

Answer 7:

Find the slopes between $A$ , $B$ , and $C$ :

$Slope of A B = \frac{2 - (- 3)}{3 - (- 2)} = \frac{5}{5} = 1$

$Slope of B C = \frac{5 - 2}{6 - 3} = \frac{3}{3} = 1$

Since the slopes are equal, the points are collinear.

Answer 8:

Using the distance formula:

$5 = \sqrt{(4 - 1)^{2} + (a - 1)^{2}}$

Solve to find $a = 5$ or $a = - 3$ .

Answer 9:

Area of triangle:

$Area = \frac{1}{2} \times 6 \times 8 = 24 square units$

Answer 10:

Using the midpoint formula:

$(- 4, - 1) = (\frac{2 + a}{2}, \frac{7 + b}{2})$

Solving, we get $a = - 10$ and $b = - 9$ .

Question: 1

Step-by-Step Solutions

Question

i. Express $- x^{2} + 6 x - 5$ in the form $a (x + b)^{2} + c$ , where $a$ , $b$ , and $c$ are constants.

ii. State the smallest possible value of $m$ for which $f$ is one-one.

iii. For the case where $m = 5$ , find an expression for $f^{- 1} (x)$ and state the domain of $f^{- 1}$ .

Solution:

i. Express $- x^{2} + 6 x - 5$ in the form $a (x + b)^{2} + c$

We begin by completing the square for the quadratic expression:

- x^{2} + 6 x - 5

Step 1: Factor out the negative sign from the first two terms:

= - (x^{2} - 6 x) - 5

Step 2: Complete the square inside the parentheses. To complete the square, take half of the coefficient of $x$ (which is $- 6$ ), square it, and add it and subtract it inside the parentheses:

= - (x^{2} - 6 x + 9 - 9) - 5

= - (x^{2} - 6 x + 9) + 9 - 5

Step 3: Factor the perfect square trinomial:

= - (x - 3)^{2} + 4

Thus, the expression in the required form is:

- x^{2} + 6 x - 5 = - (x - 3)^{2} + 4

Here, $a = - 1$ , $b = - 3$ , and $c = 4$ .

ii. State the smallest possible value of $m$ for which $f$ is one-one.

For a quadratic function to be one-one, it must either be strictly increasing or strictly decreasing. From the completed square form $f (x) = - (x - 3)^{2} + 4$ , we know that the vertex of the parabola is at $x = 3$ , and the function is decreasing for $x \leq 3$ and increasing for $x \geq 3$ . To make $f$ one-one, we restrict the domain to values of $x$ greater than or equal to the vertex.

The smallest possible value of $m$ for which $f$ is one-one is:

m = 3

iii. For the case where $m = 5$ , find an expression for $f^{- 1} (x)$ and state the domain of $f^{- 1}$ .

Given that $m = 5$ , the function $f (x) = - (x - 3)^{2} + 4$ is defined for $x \geq 5$ .

We will find the inverse function $f^{- 1} (x)$ . Start by setting $y = - (x - 3)^{2} + 4$ and solving for $x$ :

y = - (x - 3)^{2} + 4

Step 1: Subtract 4 from both sides:

y - 4 = - (x - 3)^{2}

Step 2: Multiply both sides by -1:

- (y - 4) = (x - 3)^{2}

We get

4 - y = (x - 3)^{2}

Replace x with y, and y with x

4 - x = (y - 3)^{2}

Step 3: Take the square root of both sides:

\sqrt{(4 - x)} = y - 3

Step 4: Solve for $y$ :

y = 3 + \sqrt{(4 - x)}

The inverse function is:

f^{- 1} (x) = 3 + \sqrt{(4 - x)}

The domain of the inverse function is restricted to values of $x$ for which $(4 - x) \geq 0$ , or equivalently:

x \leq 4

Final Answer:

i. $- (x - 3)^{2} + 4$

ii. $m = 3$

iii. $f^{- 1} (x) = 3 + \sqrt{(4 - x)}$ , Domain: $x \leq 4$

Question: 2

Step-by-Step Solutions

Question

The function $f : x \mapsto x^{2} - 4 x + k$ is defined for the domain $x \geq p$ , where $k$ and $p$ are constants.

i. Express $f (x)$ in the form $(x + a)^{2} + b + k$ , where $a$ and $b$ are constants.

ii. State the range of $f$ in terms of $k$ .

iii. State the smallest possible value of $p$ for which $f$ is one-one.

iv. For the value of $p$ found in part iii, find an expression for $f^{- 1} (x)$ and state the domain of $f^{- 1}$ , giving your answer in terms of $k$ .

Solution:

i. Express $f (x)$ in the form $(x + a)^{2} + b + k$

We begin by completing the square for the quadratic expression:

f (x) = x^{2} - 4 x + k

Step 1: Factor out any constants from the first two terms:

= (x^{2} - 4 x) + k

Step 2: Complete the square inside the parentheses. To complete the square, take half of the coefficient of $x$ (which is $- 4$ ), square it, and add it and subtract it inside the parentheses:

= (x^{2} - 4 x + 4 - 4) + k

= (x - 2)^{2} - 4 + k

Thus, the expression in the required form is:

f (x) = (x - 2)^{2} + k - 4

Here, $a = - 2$ , and $b = - 4$ .

ii. State the range of $f$ in terms of $k$

From the expression $f (x) = (x - 2)^{2} + k - 4$ , we know that the minimum value of $(x - 2)^{2}$ is 0, as squares are always non-negative. Therefore, the minimum value of $f (x)$ occurs when $(x - 2)^{2} = 0$ , which gives:

f_{min} = k - 4

Thus, the range of $f (x)$ is:

f (x) \geq k - 4

iii. State the smallest possible value of $p$ for which $f$ is one-one.

For a quadratic function to be one-one, we need to restrict the domain such that the function is either strictly increasing or strictly decreasing. From the expression $f (x) = (x - 2)^{2} + k - 4$ , we know that the vertex of the parabola occurs at $x = 2$ , and the function is increasing for $x \geq 2$ .

Therefore, the smallest possible value of $p$ for which $f$ is one-one is:

p = 2

iv. For the value of $p = 2$ , find an expression for $f^{- 1} (x)$ and state the domain of $f^{- 1}$ , giving your answer in terms of $k$ .

We are given that $p = 2$ , so the function $f (x) = (x - 2)^{2} + k - 4$ is defined for $x \geq 2$ .

We will find the inverse function $f^{- 1} (x)$ . Start by setting $y = (x - 2)^{2} + k - 4$ and solving for $x$ :

y = (x - 2)^{2} + k - 4

Step 1: Subtract $k - 4$ from both sides:

y - (k - 4) = (x - 2)^{2}

Step 2: Take the square root of both sides (since the domain of $f$ is restricted to $x \geq 2$ , we only take the positive square root):

\sqrt{y - (k - 4)} = x - 2

Step 3: Solve for $x$ :

x = 2 + \sqrt{y - (k - 4)}

The inverse function is:

f^{- 1} (x) = 2 + \sqrt{x - (k - 4)}

The domain of $f^{- 1} (x)$ is the range of $f (x)$ , which we found to be $f (x) \geq k - 4$ . Therefore, the domain of $f^{- 1} (x)$ is:

x \geq k - 4

Final Answer:

i. $f (x) = (x - 2)^{2} + k - 4$

ii. $f (x) \geq k - 4$

iii. $p = 2$

iv. $f^{- 1} (x) = 2 + \sqrt{x - (k - 4)}$ , Domain: $x \geq k - 4$

Question: 3

Step-by-Step Solutions

Question:

The function $f$ is defined as:

f (x) = {\begin{cases} 3 x - 2 & for - 1 \leq x \leq 1, \\ \frac{4}{5 - x} & for 1 < x \leq 4. \end{cases}

i. State the range of $f$ .

ii. Copy the diagram and sketch the graph of $y = f^{- 1} (x)$ .

iii. Obtain expressions to define the function $f^{- 1} (x)$ , giving the set of values for which each expression is valid.

Solution:

i. State the range of $f$

First, we evaluate the range of each piece of the function:

- For

- 1 \leq x \leq 1

, the function is

f (x) = 3 x - 2

. The range is found by evaluating the function at the endpoints:

f (- 1) = 3 (- 1) - 2 = - 5, f (1) = 3 (1) - 2 = 1.

Thus, the range of

3 x - 2

is

[- 5, 1]

. - For

1 < x \leq 4

, the function is

f (x) = \frac{4}{5 - x}

. We find the range by evaluating the function at the endpoints:

f (4) = \frac{4}{5 - 4} = 4, f (1^{+}) = \frac{4}{5 - 1} = 1.

So the range of

\frac{4}{5 - x}

is

(1, 4]

.

Thus, the range of the entire function $f (x)$ is:

[- 5, 4]

ii. Copy the diagram and sketch the graph of $y = f^{- 1} (x)$

The graph of the inverse function $y = f^{- 1} (x)$ is obtained by reflecting the graph of $f (x)$ over the line $y = x$ . To sketch the graph:

- The points on the graph of

f (x)

are reflected as

(x, y) \to (y, x)

. - For example,

f (- 1) = - 5

gives a point on

f^{- 1} (x)

as

(- 5, - 1)

, and

f (1) = 1

gives

(1, 1)

. - Similarly, for the second part of

f (x)

,

f (4) = 4

gives

(4, 4)

, and

f (1^{+}) = 1

reflects as

(1, 1)

.

The graph of $f^{- 1} (x)$ can now be sketched accordingly by reflecting these points and ensuring the correct piecewise behavior of the inverse function.

iii. Obtain expressions to define the function $f^{- 1} (x)$ , giving the set of values for which each expression is valid

We now need to find the inverse of each piece of $f (x)$ and specify the domain for each:

- For

f (x) = 3 x - 2

(valid for

- 1 \leq x \leq 1

): - Start with

y = 3 x - 2

. - Solve for

x

:

y + 2 = 3 x

x = \frac{y + 2}{3}

So,

f^{- 1} (x) = \frac{x + 2}{3}

, valid for

- 5 \leq x \leq 1

(since the range of

f (x)

for this piece is

[- 5, 1]

). - For

f (x) = \frac{4}{5 - x}

(valid for

1 < x \leq 4

): - Start with

y = \frac{4}{5 - x}

. - Solve for

x

:

y (5 - x) = 4

5 - x = \frac{4}{y}

x = 5 - \frac{4}{y}

So,

f^{- 1} (x) = 5 - \frac{4}{x}

, valid for

1 < x \leq 4

.

Final Answer:

i. Range of $f (x)$ : $[- 5, 4]$

ii. See graph of $y = f^{- 1} (x)$ , which is the reflection of $f (x)$ over the line $y = x$ .

iii. The inverse function is:

f^{- 1} (x) = {\begin{cases} \frac{x + 2}{3} & for - 5 \leq x \leq 1, \\ 5 - \frac{4}{x} & for 1 < x \leq 4. \end{cases}

Graph

Step-by-Step Solutions

Question:

The function $f (x) = 2 x^{2} - 12 x + 13$ is defined as follows:

i. Express $2 x^{2} - 12 x + 13$ in the form $a (x + b)^{2} + c$ , where $a$ , $b$ , and $c$ are constants.

Solution:

We will complete the square to express the quadratic in the required form:

f (x) = 2 (x^{2} - 6 x) + 13

Now, complete the square for $x^{2} - 6 x$ :

x^{2} - 6 x = (x - 3)^{2} - 9

Thus:

f (x) = 2 ((x - 3)^{2} - 9) + 13

Simplifying:

f (x) = 2 (x - 3)^{2} - 18 + 13

f (x) = 2 (x - 3)^{2} - 5

Thus, the expression in the required form is:

f (x) = 2 (x - 3)^{2} - 5

ii. The function $f (x) = 2 x^{2} - 12 x + 13$ is defined for $x \geq k$ , where $k$ is a constant. It is given that $f$ is a one-to-one function. State the smallest possible value of $k$ .

In order for the quadratic function to be one-to-one, we need to restrict the domain so that the function is either strictly increasing or strictly decreasing. The function $f (x) = 2 (x - 3)^{2} - 5$ has a minimum value when $x = 3$ , which is the vertex of the parabola.

To make $f$ one-to-one, we restrict the domain to $x \geq 3$ , so that the function is strictly increasing. Thus, the smallest possible value of $k$ is:

k = 3

iii. Find the range of $f$ .

The range of $f (x) = 2 (x - 3)^{2} - 5$ is determined by the fact that the minimum value of $(x - 3)^{2}$ is 0, since squares are always non-negative.

Thus, the minimum value of $f (x)$ is:

f_{min} = 2 (0) - 5 = - 5

Since the function is strictly increasing for $x \geq 3$ , the range of $f (x)$ is:

f (x) \geq - 5

iv. Find the expression for $f^{- 1} (x)$ and state the domain of $f^{- 1}$ .

We start by setting $y = 2 (x - 3)^{2} - 5$ and solve for $x$ :

y + 5 = 2 (x - 3)^{2}

\frac{y + 5}{2} = (x - 3)^{2}

Now, take the square root of both sides:

\sqrt{\frac{y + 5}{2}} = x - 3

\p>Thus, the expression for

f^{- 1} (x)

is:

f^{- 1} (x) = 3 + \sqrt{\frac{x + 5}{2}}

Since $f (x)$ is defined for $x \geq 3$ , the domain of $f^{- 1} (x)$ is the range of $f (x)$ , which is $x \geq - 5$ . Thus, the domain of $f^{- 1} (x)$ is:

x \geq - 5

Question

i. Express $x^{2} - 2 x - 15$ in the form $(x + a)^{2} + b$ .

Solution:

We will complete the square for the expression $x^{2} - 2 x - 15$ .

Step 1: Take the quadratic part $x^{2} - 2 x$ and complete the square:

x^{2} - 2 x = (x - 1)^{2} - 1

Step 2: Substitute this back into the original expression:

x^{2} - 2 x - 15 = (x - 1)^{2} - 1 - 15

= (x - 1)^{2} - 16

Thus, the expression in the required form is:

f (x) = (x - 1)^{2} - 16

---

ii. State the smallest possible value of $c$ .

Since $f (x) = (x - 1)^{2} - 16$ , the minimum value of $(x - 1)^{2}$ is 0 (because squares are non-negative). Therefore, the smallest value of $f (x)$ is:

f_{min} = - 16

Thus, the smallest possible value of $c$ is:

c = - 16

---

iii. For the case where $c = 9$ and $d = 65$ , find $p$ and $q$ .

We are given that $f (x)$ is bounded between 9 and 65. From the equation $f (x) = (x - 1)^{2} - 16$ , set $f (x) = 9$ and solve for $x$ :

(x - 1)^{2} - 16 = 9

(x - 1)^{2} = 25

x - 1 = \pm 5

x = 1 \pm 5

x = 6 or x = - 4

So, $p = - 4$ and $q = 6$ .

---

iv. Find an expression for $f^{- 1} (x)$ and state the domain of $f^{- 1}$ .

To find the inverse function $f^{- 1} (x)$ , we start by setting $y = (x - 1)^{2} - 16$ and solve for $x$ :

y + 16 = (x - 1)^{2}

Take the square root of both sides:

x - 1 = \pm \sqrt{y + 16}

So:

x = 1 \pm \sqrt{y + 16}

Since $f (x)$ is defined for $x \geq - 4$ , we take the positive square root:

f^{- 1} (x) = 1 + \sqrt{x + 16}

The domain of $f^{- 1} (x)$ is the range of $f (x)$ , which is $9 \leq x \leq 65$ . Therefore, the domain of $f^{- 1} (x)$ is:

9 \leq x \leq 65

Question

Step-by-Step Solution

i. Express $f (x)$ in the form $a (x - b)^{2} - c$

We are given the function:

f (x) = 2 x^{2} - 12 x + 7

To express $f (x)$ in the form $a (x - b)^{2} - c$ , we need to complete the square.

Step 1: Factor out 2 from the quadratic terms:

f (x) = 2 (x^{2} - 6 x) + 7

Step 2: Complete the square for the expression inside the parentheses:

x^{2} - 6 x = (x - 3)^{2} - 9

Substitute this back into the equation:

f (x) = 2 ((x - 3)^{2} - 9) + 7

Step 3: Simplify the expression:

f (x) = 2 (x - 3)^{2} - 18 + 7

f (x) = 2 (x - 3)^{2} - 11

Thus, the expression in the required form is:

f (x) = 2 (x - 3)^{2} - 11

ii. State the range of $f$

The function $f (x) = 2 (x - 3)^{2} - 11$ is a parabola that opens upwards (since the coefficient of $(x - 3)^{2}$ is positive).

The minimum value of $f (x)$ occurs when $(x - 3)^{2} = 0$ , which gives:

f_{min} = 2 (0) - 11 = - 11

Therefore, the range of $f (x)$ is:

f (x) \geq - 11

iii. Find the set of values of $x$ for which $f (x) < 21$

We are given that $f (x) = 2 (x - 3)^{2} - 11$ , and we need to find the values of $x$ for which $f (x) < 21$ .

Step 1: Set the inequality:

2 (x - 3)^{2} - 11 < 21

Step 2: Add 11 to both sides:

2 (x - 3)^{2} < 32

Step 3: Divide both sides by 2:

(x - 3)^{2} < 16

Step 4: Take the square root of both sides:

- 4 < x - 3 < 4

Step 5: Solve for $x$ :

- 4 + 3 < x < 4 + 3

- 1 < x < 7

Therefore, the set of values of $x$ for which $f (x) < 21$ is:

x \in (- 1, 7)

iv. Find the value of the constant $k$ for which the equation $g (f (x)) = 0$ has two equal roots

We are given that $g (x) = 2 x + k$ and need to find $k$ such that $g (f (x)) = 0$ has two equal roots.

First, express $g (f (x)) = 0$ :

g (f (x)) = 2 f (x) + k = 0

Substitute $f (x) = 2 (x - 3)^{2} - 11$ into the equation:

2 (2 (x - 3)^{2} - 11) + k = 0

Simplify:

4 (x - 3)^{2} - 22 + k = 0

4 (x - 3)^{2} + k = 22

For the equation to have two equal roots, the expression inside the parentheses $(x - 3)^{2}$ must be zero, which occurs when $x = 3$ .

Substitute $x = 3$ into the equation:

4 (0) + k = 22

Thus, $k = 22$ .

Notes on Parallel and Perpendicular Lines

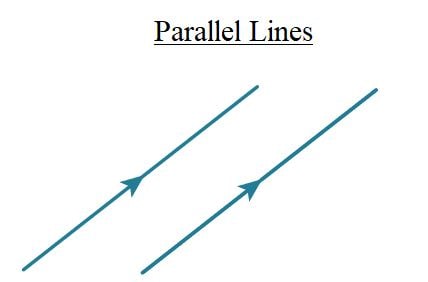
1. Parallel Lines

Definition: Parallel lines are two or more lines in the same plane that never intersect. They remain equidistant from each other at all points.

Properties of Parallel Lines:

Parallel lines have the same slope.
If two lines are parallel, their slopes are equal.
The y-intercepts of parallel lines may be different.

Slope Condition for Parallel Lines:

Let the slopes of two lines be $m_{1}$ and $m_{2}$ . For the lines to be parallel, their slopes must be equal:

$m_{1} = m_{2}$

Equation of Parallel Lines:

Two parallel lines can be represented as:

First line: $y = m_{1} x + c_{1}$
Second line: $y = m_{2} x + c_{2}$

If $m_{1} = m_{2}$ , the lines are parallel, but the constants $c_{1}$ and $c_{2}$ determine the vertical positions of the lines.

Example:

Consider the lines $y = 2 x + 3$ and $y = 2 x - 5$ . Both lines have the same slope $m = 2$ , which means they are parallel. However, they have different y-intercepts.

Perpendicular Lines

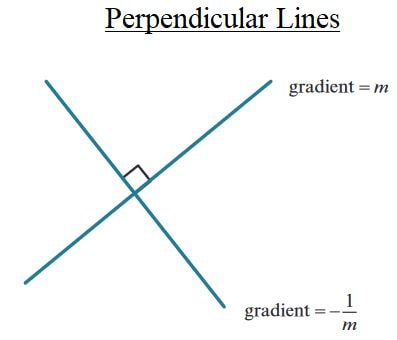
2. Perpendicular Lines

Definition: Perpendicular lines are two lines that intersect at a right angle (90°). Their slopes have a specific relationship: the product of their slopes is $- 1$ .

Properties of Perpendicular Lines:

Perpendicular lines intersect at 90°.
The slopes of two perpendicular lines are negative reciprocals of each other.
If one line has a slope of $m$ , the slope of the perpendicular line is $- \frac{1}{m}$ .

Slope Condition for Perpendicular Lines:

Let the slopes of two lines be $m_{1}$ and $m_{2}$ . For the lines to be perpendicular, the product of their slopes must be $- 1$ :

$m_{1} \times m_{2} = - 1$

Equation of Perpendicular Lines:

If one line has the equation $y = m_{1} x + c_{1}$ and another line is perpendicular to it, the slope of the perpendicular line will be $- \frac{1}{m_{1}}$ . Thus, the equation of the perpendicular line will be:

$y = - \frac{1}{m_{1}} x + c_{2}$

Example:

Consider the lines $y = \frac{3}{4} x + 2$ and $y = - \frac{4}{3} x + 5$ . Since the product of the slopes $\frac{3}{4} \times - \frac{4}{3} = - 1$ , the lines are perpendicular.

3. Parallel and Perpendicular Line Relationships

The relationship between parallel and perpendicular lines is important in both geometry and algebra:

Parallel lines have equal slopes, but different y-intercepts (unless they are the same line).
Perpendicular lines have slopes that are negative reciprocals of each other.

Summary of Conditions:

For two lines:

If $m_{1} = m_{2}$ , the lines are parallel.
If $m_{1} \times m_{2} = - 1$ , the lines are perpendicular.

4. Distance Between Two Parallel Lines

The shortest distance between two parallel lines $y = m_{1} x + c_{1}$ and $y = m_{1} x + c_{2}$ is given by:

$d = \frac{| c_{2} - c_{1} |}{\sqrt{1 + m_{1}^{2}}}$

Example:

Consider the lines $y = 2 x + 3$ and $y = 2 x - 4$ . The distance between these two parallel lines is:

$d = \frac{| 3 - (- 4) |}{\sqrt{1 + 2^{2}}} = \frac{7}{\sqrt{5}}$

Example: Find the distance of the point $(4, - 6)$ from the line $2 x - 7 y - 24 = 0$ .

Solution: The given line is $2 x - 7 y - 24 = 0$ .

Comparing with the general equation of a line $A x + B y + C = 0$ , we get $A = 2$ , $B = - 7$ , and $C = - 24$ .

Given point is $(x_{1}, y_{1}) = (4, - 6)$ .

The distance of the given point from the given line is $d = \frac{| A x_{1} + B y_{1} + C |}{\sqrt{A^{2} + B^{2}}} = \frac{| 2 \cdot 4 - 7 \cdot (- 6) - 24 |}{\sqrt{2^{2} + (- 7)^{2}}} = 3.6$ .

Example: Estimate the distance between the two parallel lines $y = 2 x + 7$ and $y = 2 x + 5$ .

Solution: The distance between two parallel lines is given by $\frac{| c_{1} - c_{2} |}{\sqrt{a^{2} + b^{2}}}$ .

Here, the equations of parallel lines are $y = 2 x + 7$ and $y = 2 x + 5$ .

Slopes are the same $m_{2} = m_{1} = 2$ and $c_{1} = 7$ , $c_{2} = 5$ .

So, the distance between two parallel lines is given by, $Distance = \frac{| c_{1} - c_{2} |}{\sqrt{a^{2} + b^{2}}} = \frac{| 7 - 5 |}{\sqrt{2^{2} + 1^{2}}} = \frac{2}{\sqrt{5}}$

Example:

Example 5: Let $P S$ be the median of the triangle with vertices $P (2, 2)$ , $Q (6, - 1)$ , and $R (7, 3)$ . The equation of the line passing through $(1, - 1)$ and parallel to $P S$ is:

A) $2 x - 9 y - 7 = 0$
B) $2 x - 9 y - 11 = 0$
C) $2 x + 9 y - 11 = 0$
D) $2 x + 9 y + 7 = 0$

Solution:

$S$ is the midpoint of $Q R$ : $S = (\frac{6 + 7}{2}, \frac{- 1 + 3}{2}) = (\frac{13}{2}, 1)$

Slope of $P S$ : $Slope of P S = \frac{1 - 2}{\frac{13}{2} - 2} = \frac{- 1}{\frac{9}{2}} = - \frac{2}{9}$

Equation of line passing through $(x_{1}, y_{1})$ having slope $m$ is $y - y_{1} = m (x - x_{1})$ . The required equation is: $y + 1 = - \frac{2}{9} (x - 1)$ Simplifying, we get: $2 x + 9 y + 7 = 0$

Hence, Option D is the answer.

5. Perpendicular Bisector

The perpendicular bisector of a line segment is the line that divides the segment into two equal parts and is perpendicular to the segment.

Equation of the Perpendicular Bisector:

To find the equation of the perpendicular bisector of the segment joining two points $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ , follow these steps:

Find the midpoint of the segment:

$(\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$

Find the slope of the line segment:

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

The slope of the perpendicular bisector is the negative reciprocal of this slope:

$m_{bisector} = - \frac{1}{m}$

Example:

Find the equation of the perpendicular bisector of the segment joining the points $(2, 3)$ and $(6, 7)$ .

Solution:

Midpoint: $(\frac{2 + 6}{2}, \frac{3 + 7}{2}) = (4, 5)$
Slope of the segment: $m = \frac{7 - 3}{6 - 2} = 1$
Slope of the perpendicular bisector: $m_{bisector} = - 1$
Equation of the perpendicular bisector: $y - 5 = - 1 (x - 4)$ , or $y = - x + 9$ .

Question:

The coordinates of three points are $A (k - 5, - 15)$ , $B (10, k)$ , and $C (6, - k)$ . Find the two possible values of $k$ if $A$ , $B$ , and $C$ are collinear.

Answer:

If $A$ , $B$ , and $C$ are collinear, then they lie on the same line. Thus, the gradient of $A B$ must equal the gradient of $B C$ :

$\frac{- 15 - k}{k - 15} = \frac{k + k}{10 - 6}$ $\begin{aligned} Simplify: & \frac{- 15 - k}{k - 15} = \frac{2 k}{4} \\ Cross-multiply: & 4 (- 15 - k) = 2 k (k - 15) \\ Expand brackets: & - 60 - 4 k = 2 k^{2} - 30 k \\ Collect terms on one side: & 2 k^{2} - 26 k - 60 = 0 \\ Factorise: & 2 (k^{2} - 13 k - 30) = 0 \\ Solve: & (k - 3) (k - 10) = 0 \end{aligned}$

Thus, $k = 3$ or $k = 10$ .

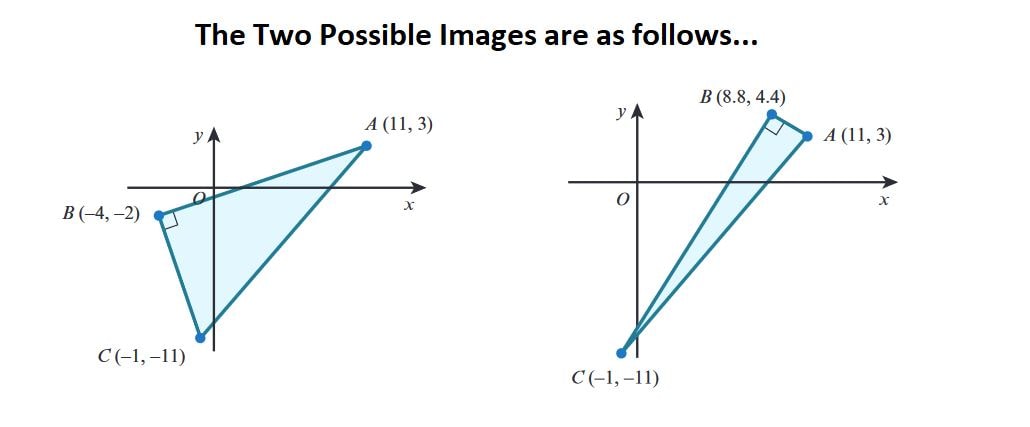
Example

The vertices of triangle $A B C$ are $A (1, 3)$ , $B (2 k, k)$ , and $C (- 1, - 1)$ . Find the two possible values of $k$ if angle $A B C$ is $90^{\circ}$ .

Answer:

Since angle $A B C$ is $90^{\circ}$ , the product of the gradients of $A B$ and $B C$ must be $- 1$ :

$\frac{k - 3}{2 k - 11} \times \frac{- 11 - k}{- 1 - 2 k} = - 1$

Cross-multiply to equate with $- 1$ : $\frac{k - 3}{2 k - 11} = \frac{- 1}{\frac{- 11 - k}{- 1 - 2 k}} ⟹ \frac{k - 3}{2 k - 11} = \frac{k + 11}{2 k + 1}$

Clear the denominator: $(k - 3) (2 k + 1) = (2 k - 11) (k + 11)$

Expand and simplify: $2 k^{2} + k - 3 = 2 k^{2} + 9 k - 121$ $12 k = 118 ⟹ k = \frac{118}{12} \approx 9.83$

Upon re-evaluation (solving a quadratic equation derived from above expansions): $5 k^{2} - 12 k - 44 = 0 ⟹ (5 k - 22) (k + 2) = 0$

Solve for $k$ : $k = \frac{22}{5} or k = - 2$

Thus, $k = 4.4$ or $k = - 2$ .

Reflections in Graphs: Detailed Notes

Understanding Reflections

Reflection: A transformation that "flips" a graph over a specified line, such as the x-axis or y-axis, producing a mirror image of the original graph. The most common types of reflections are:

Reflection over the x-axis: This type of reflection is achieved by multiplying the entire function by $- 1$ . If the original function is $y = f (x)$ , then the reflected function is $y = - f (x)$ .

Reflection over the y-axis: This type of reflection is achieved by replacing $x$ with $- x$ in the function. If the original function is $y = f (x)$ , then the reflected function is $y = f (- x)$ .

Example: Reflection Over the x-axis

Consider the function $y = x^{2} - 2 x + 1$ . The reflection of this function over the x-axis can be found by multiplying the entire function by $- 1$ .

The original function is:

y = x^{2} - 2 x + 1

The reflected function is:

y = - (x^{2} - 2 x + 1) = - x^{2} + 2 x - 1

When these two functions are graphed, they are mirror images of each other across the x-axis. This means that for every point $(x, y)$ on the original graph, there is a corresponding point $(x, - y)$ on the reflected graph.

Key Observations:

For every $x$ value, the y-coordinates of the reflected graph are the negative of the y-coordinates of the original graph.

The shapes of the original graph and the reflected graph are identical, but they are positioned on opposite sides of the x-axis.

Example: Reflection Over the y-axis

Consider the function $y = (x - 3)^{2} + 2$ . The reflection of this function over the y-axis can be found by replacing $x$ with $- x$ in the function.

The original function is:

y = (x - 3)^{2} + 2

The reflected function is:

y = (- x - 3)^{2} + 2

This operation reflects the graph over the y-axis. The result is that for every point $(x, y)$ on the original graph, there is a corresponding point $(- x, y)$ on the reflected graph.

Key Observations:

The y-coordinates remain unchanged, but the x-coordinates are the negative of those in the original graph.

The shapes of the original graph and the reflected graph are identical, but they are positioned on opposite sides of the y-axis.

Conclusion:

Reflections are a fundamental type of transformation that can be used to understand how graphs behave under certain operations. By reflecting a graph over the x-axis or y-axis, we can visualize how the graph would look if flipped across these axes. This concept is widely used in various mathematical applications and helps in understanding symmetry in functions.

Solved Examples

Reflections: Step-by-Step Solutions

Problem 2a:

Find the equation of the graph $y = 5 x^{2}$ after reflection in the x-axis.

Steps:

1. Original Function:

y = 5 x^{2}

2. Reflection in the x-axis:

To reflect the graph over the x-axis, multiply the entire function by $- 1$ :

y = - 5 x^{2}

Final Answer:

y = - 5 x^{2}

Problem 2b:

Find the equation of the graph $y = 2 x^{4}$ after reflection in the y-axis.

Steps:

1. Original Function:

y = 2 x^{4}

2. Reflection in the y-axis:

To reflect the graph over the y-axis, replace $x$ with $- x$ in the function:

y = 2 (- x)^{4}

3. Simplify:

Since $(- x)^{4} = x^{4}$ , the equation remains the same:

y = 2 x^{4}

Final Answer:

y = 2 x^{4}

(Note: The reflection over the y-axis does not change the graph because $x^{4}$ is an even function.)

Problem 2c:

Find the equation of the graph $y = 2 x^{2} - 3 x + 1$ after reflection in the y-axis.

Steps:

1. Original Function:

y = 2 x^{2} - 3 x + 1

2. Reflection in the y-axis:

To reflect the graph over the y-axis, replace $x$ with $- x$ in the function:

y = 2 (- x)^{2} - 3 (- x) + 1

3. Simplify:

Simplify each term:

y = 2 x^{2} + 3 x + 1

Final Answer:

y = 2 x^{2} + 3 x + 1

Problem 2d:

Find the equation of the graph $y = 5 + 2 x - 3 x^{2}$ after reflection in the x-axis.

Steps:

1. Original Function:

y = 5 + 2 x - 3 x^{2}

2. Reflection in the x-axis:

To reflect the graph over the x-axis, multiply the entire function by $- 1$ :

y = - (5 + 2 x - 3 x^{2})

3. Distribute $- 1$ :

Distribute the negative sign across the function:

y = - 5 - 2 x + 3 x^{2}

Final Answer:

y = 3 x^{2} - 2 x - 5

Transformation Descriptions: Step-by-Step Solutions

Problem 3a:

Describe the transformation that maps the graph $y = x^{2} + 7 x - 3$ onto the graph $y = - x^{2} - 7 x + 3$ .

Steps:

1. Compare the Original and Transformed Functions:

y = x^{2} + 7 x - 3

y = - x^{2} - 7 x + 3

2. Identify the Transformation:

Notice that the entire function has been multiplied by $- 1$ , which indicates a reflection over the x-axis.

Final Answer:

The transformation that maps the original graph onto the new graph is a reflection over the x-axis.

Problem 3b:

Describe the transformation that maps the graph $y = x^{2} - 3 x + 4$ onto the graph $y = x^{2} + 3 x + 4$ .

Steps:

1. Compare the Original and Transformed Functions:

y = x^{2} - 3 x + 4

y = x^{2} + 3 x + 4

2. Identify the Transformation:

Notice that the sign of the linear term $- 3 x$ has changed to $+ 3 x$ , which indicates a reflection over the y-axis.

Final Answer:

The transformation that maps the original graph onto the new graph is a reflection over the y-axis.

Problem 3c:

Describe the transformation that maps the graph $y = 2 x - 5 x^{2}$ onto the graph $y = 5 x^{2} - 2 x$ .

Steps:

1. Compare the Original and Transformed Functions:

y = 2 x - 5 x^{2}

y = 5 x^{2} - 2 x

2. Identify the Transformation:

Notice that the terms in the function have been reordered, with their signs reversed. This transformation involves both a reflection over the y-axis and a rearrangement of the terms.

Final Answer:

The transformation that maps the original graph onto the new graph is a reflection over the y-axis followed by rearranging the terms.

Problem 3d:

Describe the transformation that maps the graph $y = x^{3} + 2 x^{2} - 3 x + 1$ onto the graph $y = - x^{3} - 2 x^{2} + 3 x - 1$ .

Steps:

1. Compare the Original and Transformed Functions:

y = x^{3} + 2 x^{2} - 3 x + 1

y = - x^{3} - 2 x^{2} + 3 x - 1

2. Identify the Transformation:

Notice that the entire function has been multiplied by $- 1$ , which indicates a reflection over the x-axis.

Final Answer:

The transformation that maps the original graph onto the new graph is a reflection over the x-axis.

Question:

Find the equation of the perpendicular bisector of the line segment joining $A (- 5, 1)$ and $B (7, - 2)$ .

Answer:

Step 1: Calculate the gradient of $A B$ :

$Gradient of A B = \frac{- 2 - 1}{7 - (- 5)} = \frac{- 3}{12} = - \frac{1}{4}$

Step 2: Find the gradient of the perpendicular bisector (negative reciprocal):

$Gradient of the perpendicular bisector = 4$

Step 3: Find the midpoint of $A B$ :

$Midpoint of A B = (\frac{- 5 + 7}{2}, \frac{1 + (- 2)}{2}) = (1, - \frac{1}{2})$

Step 4: Use the point-slope form to find the equation of the perpendicular bisector:

$y - y_{1} = m (x - x_{1})$

Substitute $x_{1} = 1$ , $y_{1} = - \frac{1}{2}$ , and $m = 4$ :

$y + \frac{1}{2} = 4 (x - 1)$

Step 5: Simplify and expand:

$y + \frac{1}{2} = 4 x - 4$

Step 6: Multiply both sides by 2 to remove the fraction:

$2 y + 1 = 8 x - 8$

Final equation of the perpendicular bisector:

$2 y = 8 x - 9$

Question 1:

Find the equation of the line with:

Gradient 2 passing through the point $(4, 9)$

Solution:

The equation of the line is given by the point-slope form:

y - y_{1} = m (x - x_{1})

Substitute $m = 2$ , $x_{1} = 4$ , and $y_{1} = 9$ :

y - 9 = 2 (x - 4)

Expand:

y - 9 = 2 x - 8

Simplify:

y = 2 x + 1

Gradient $- 3$ passing through the point $(1, - 4)$

Solution:

y - y_{1} = m (x - x_{1})

Substitute $m = - 3$ , $x_{1} = 1$ , and $y_{1} = - 4$ :

y + 4 = - 3 (x - 1)

Expand:

y + 4 = - 3 x + 3

Simplify:

y = - 3 x - 1

Gradient $- \frac{2}{3}$ passing through the point $(- 4, 3)$

Solution:

y - y_{1} = m (x - x_{1})

Substitute $m = - \frac{2}{3}$ , $x_{1} = - 4$ , and $y_{1} = 3$ :

y - 3 = - \frac{2}{3} (x + 4)

Expand:

y - 3 = - \frac{2}{3} x - \frac{8}{3}

Simplify:

y = - \frac{2}{3} x + \frac{1}{3}

Question 2:

Find the equation of the line passing through each pair of points:

Points $(1, 0)$ and $(5, 6)$

Solution:

Step 1: Calculate the gradient:

m = \frac{6 - 0}{5 - 1} = \frac{6}{4} = \frac{3}{2}

Step 2: Use point-slope form with $x_{1} = 1$ and $y_{1} = 0$ :

y - 0 = \frac{3}{2} (x - 1)

Expand:

y = \frac{3}{2} x - \frac{3}{2}

Points $(3, - 5)$ and $(- 2, 4)$

Solution:

Step 1: Calculate the gradient:

m = \frac{4 - (- 5)}{- 2 - 3} = \frac{9}{- 5} = - \frac{9}{5}

Step 2: Use point-slope form with $x_{1} = 3$ and $y_{1} = - 5$ :

y + 5 = - \frac{9}{5} (x - 3)

Expand:

y + 5 = - \frac{9}{5} x + \frac{27}{5}

Simplify:

y = - \frac{9}{5} x - \frac{2}{5}

Points $(3, - 1)$ and $(- 3, - 5)$

Solution:

Step 1: Calculate the gradient:

m = \frac{- 5 - (- 1)}{- 3 - 3} = \frac{- 4}{- 6} = \frac{2}{3}

Step 2: Use point-slope form with $x_{1} = 3$ and $y_{1} = - 1$ :

y + 1 = \frac{2}{3} (x - 3)

Expand:

y + 1 = \frac{2}{3} x - 2

Simplify:

y = \frac{2}{3} x - 3

Question 3:

Find the equation of the line:

Parallel to the line $y = 3 x - 5$ , passing through the point $(1, 7)$

Solution:

The gradient of the required line is the same as that of $y = 3 x - 5$ , which is 3. Using point-slope form:

y - 7 = 3 (x - 1)

Expand:

y - 7 = 3 x - 3

Simplify:

y = 3 x + 4

Parallel to the line $x + 2 y = 6$ , passing through the point $(4, - 6)$

Solution:

Step 1: Rearrange $x + 2 y = 6$ into slope-intercept form:

2 y = - x + 6 ⟹ y = - \frac{1}{2} x + 3

Step 2: Use the same gradient $- \frac{1}{2}$ and point-slope form:

y + 6 = - \frac{1}{2} (x - 4)

Expand:

y + 6 = - \frac{1}{2} x + 2

Simplify:

y = - \frac{1}{2} x - 4

Perpendicular to the line $y = 2 x - 3$ , passing through the point $(6, 1)$

Solution:

The gradient of the perpendicular line is the negative reciprocal of 2, which is $- \frac{1}{2}$ . Using point-slope form:

y - 1 = - \frac{1}{2} (x - 6)

Expand:

y - 1 = - \frac{1}{2} x + 3

Simplify:

y = - \frac{1}{2} x + 4

Perpendicular to the line $2 x - 3 y = 12$ , passing through the point $(8, - 3)$

Solution:

Step 1: Rearrange $2 x - 3 y = 12$ into slope-intercept form:

3 y = 2 x - 12 ⟹ y = \frac{2}{3} x - 4

Step 2: The gradient of the perpendicular line is $- \frac{3}{2}$ . Using point-slope form:

y + 3 = - \frac{3}{2} (x - 8)

Expand:

y + 3 = - \frac{3}{2} x + 12

Simplify:

y = - \frac{3}{2} x + 9

Question 4:

Find the equation of the perpendicular bisector of the line segment joining the points:

Points $(5, 2)$ and $(- 3, 6)$

Solution:

Step 1: Find the midpoint:

Midpoint = (\frac{5 + (- 3)}{2}, \frac{2 + 6}{2}) = (1, 4)

Step 2: Find the gradient of the line segment:

m = \frac{6 - 2}{- 3 - 5} = \frac{4}{- 8} = - \frac{1}{2}

Step 3: The gradient of the perpendicular bisector is 2. Use point-slope form with the midpoint $(1, 4)$ :

y - 4 = 2 (x - 1)

Expand:

y - 4 = 2 x - 2

Simplify:

y = 2 x + 2

Question 5:

The line $l_{1}$ passes through the points $P (- 10, 1)$ and $Q (2, 10)$ . The line $l_{2}$ is parallel to $l_{1}$ and passes through the point $(4, - 1)$ . The point $R$ lies on $l_{2}$ , such that $Q R$ is perpendicular to $l_{2}$ . Find the coordinates of $R$ .

Solution:

Step 1: Find the gradient of $l_{1}$ :

m_{l_{1}} = \frac{10 - 1}{2 - (- 10)} = \frac{9}{12} = \frac{3}{4}

Step 2: The gradient of $l_{2}$ is the same as that of $l_{1}$ because they are parallel:

m_{l_{2}} = \frac{3}{4}

Step 3: Use the point-slope form to find the equation of $l_{2}$ , using the point $(4, - 1)$ :

y + 1 = \frac{3}{4} (x - 4)

Expand:

y + 1 = \frac{3}{4} x - 3

Simplify:

y = \frac{3}{4} x - 4

Step 4: The gradient of $Q R$ is the negative reciprocal of $\frac{3}{4}$ , which is $- \frac{4}{3}$ . Use the point-slope form with point $Q (2, 10)$ :

y - 10 = - \frac{4}{3} (x - 2)

Expand:

y - 10 = - \frac{4}{3} x + \frac{8}{3}

Simplify:

y = - \frac{4}{3} x + \frac{38}{3}

Step 5: Solve the system of equations to find the coordinates of $R$ . Set the equations of $l_{2}$ and $Q R$ equal to each other:

\frac{3}{4} x - 4 = - \frac{4}{3} x + \frac{38}{3}

Multiply through by 12 to eliminate fractions:

9 x - 48 = - 16 x + 152

Solve for $x$ :

25 x = 200 ⟹ x = 8

Step 6: Substitute $x = 8$ into the equation of $l_{2}$ :

y = \frac{3}{4} (8) - 4 = 6 - 4 = 2

Thus, the coordinates of $R$ are $(8, 2)$ .

Question 6:

Given $P (- 4, 2)$ and $Q (5, - 4)$ , a line $l$ is drawn through $P$ and perpendicular to $P Q$ to meet the y-axis at $R$ .

Find the equation of the line $l$ .

Solution:

Step 1: Find the gradient of $P Q$ :

m_{P Q} = \frac{- 4 - 2}{5 - (- 4)} = \frac{- 6}{9} = - \frac{2}{3}

Step 2: The gradient of the perpendicular line is $\frac{3}{2}$ . Using the point-slope form with $P (- 4, 2)$ :

y - 2 = \frac{3}{2} (x + 4)

Expand:

y - 2 = \frac{3}{2} x + 6

Simplify:

y = \frac{3}{2} x + 8

Find the coordinates of $R$ .

Solution:

The point $R$ lies on the y-axis, where $x = 0$ . Substitute $x = 0$ into the equation of $l$ :

y = \frac{3}{2} (0) + 8 = 8

Thus, the coordinates of $R$ are $(0, 8)$ .

Find the area of triangle $P Q R$ .

Solution:

The area of a triangle is given by:

Area = \frac{1}{2} | x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2}) |

Substitute $P (- 4, 2)$ , $Q (5, - 4)$ , and $R (0, 8)$ :

Area = \frac{1}{2} | - 4 (- 4 - 8) + 5 (8 - 2) + 0 (2 + 4) |

= \frac{1}{2} | - 4 (- 12) + 5 (6) |

= \frac{1}{2} (48 + 30) = \frac{1}{2} (78) = 39

Thus, the area of triangle $P Q R$ is 39 square units.

Question 7:

The line $l_{1}$ has equation $3 x - 2 y = 12$ , and the line $l_{2}$ has equation $y = 15 - 2 x$ . The lines intersect at point $A$ .

Find the coordinates of $A$ .

Solution:

Step 1: Substitute $y = 15 - 2 x$ into $3 x - 2 y = 12$ :

3 x - 2 (15 - 2 x) = 12

Expand:

3 x - 30 + 4 x = 12 ⟹ 7 x = 42 ⟹ x = 6

Step 2: Substitute $x = 6$ into $y = 15 - 2 x$ :

y = 15 - 2 (6) = 3

Thus, the coordinates of $A$ are $(6, 3)$ .

Find the equation of the line through $A$ that is perpendicular to $l_{1}$ .

Solution:

The gradient of $l_{1}$ is $\frac{3}{2}$ , so the gradient of the perpendicular line is $- \frac{2}{3}$ . Use point-slope form with $A (6, 3)$ :

y - 3 = - \frac{2}{3} (x - 6)

Expand:

y - 3 = - \frac{2}{3} x + 4

Simplify:

y = - \frac{2}{3} x + 7

Question 8:

The perpendicular bisector of the line joining $A (- 10, 5)$ and $B (- 2, - 1)$ intersects the x-axis at $P$ and the y-axis at $Q$ .

Find the equation of the line $P Q$ .

Solution:

Step 1: Find the midpoint of $A B$ :

Midpoint = (\frac{- 10 + (- 2)}{2}, \frac{5 + (- 1)}{2}) = (- 6, 2)

Step 2: Find the gradient of $A B$ :

m_{A B} = \frac{- 1 - 5}{- 2 - (- 10)} = \frac{- 6}{8} = - \frac{3}{4}

Step 3: The gradient of the perpendicular bisector is the negative reciprocal of $- \frac{3}{4}$ , which is $\frac{4}{3}$ . Use point-slope form with the midpoint $(- 6, 2)$ :

y - 2 = \frac{4}{3} (x + 6)

Expand:

y - 2 = \frac{4}{3} x + 8

Simplify:

y = \frac{4}{3} x + 10

Find the coordinates of $P$ and $Q$ .

Solution:

For $P$ (intersection with the x-axis), $y = 0$ :

0 = \frac{4}{3} x + 10 ⟹ x = - \frac{30}{4} = - 7.5

Thus, $P (- 7.5, 0)$ .

For $Q$ (intersection with the y-axis), $x = 0$ :

y = \frac{4}{3} (0) + 10 = 10

Thus, $Q (0, 10)$ .

Find the length of $P Q$ .

Solution:

Use the distance formula between $P (- 7.5, 0)$ and $Q (0, 10)$ :

P Q = \sqrt{(0 - (- 7.5))^{2} + (10 - 0)^{2}} = \sqrt{{7.5}^{2} + 10^{2}} = \sqrt{56.25 + 100} = \sqrt{156.25} = 12.5

Thus, the length of $P Q$ is 12.5 units.

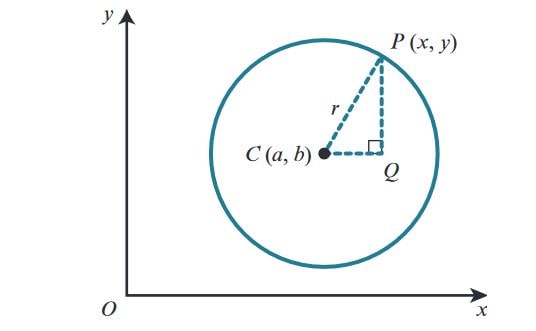
The standard form of the equation of a circle is:

$(x - h)^{2} + (y - k)^{2} = r^{2}$

Where:

$(h, k)$ is the center of the circle.
$r$ is the radius of the circle.

Steps for Finding the Center and Radius

1. Recognize the Equation of a Circle:

If the equation is of the form $x^{2} + y^{2} = r^{2}$ , it represents a circle centered at the origin $(0, 0)$ with radius $r$ .
If the equation is of the form $(x - h)^{2} + (y - k)^{2} = r^{2}$ , the center is $(h, k)$ and the radius is $r$ .

Example A

Consider the equation $x^{2} + y^{2} = 25$ :

$x^{2} + y^{2} = 25$

This is a standard form of a circle centered at the origin, $(0, 0)$ , and the radius $r$ is:

$r = \sqrt{25} = 5$

Thus, the center is $(0, 0)$ and the radius is $5$ .

Example B

Now, consider the equation $(x - 2)^{2} + (y - 1)^{2} = 9$ :

$(x - 2)^{2} + (y - 1)^{2} = 9$

From the equation, the center $(h, k)$ is $(2, 1)$ and the radius $r$ is:

$r = \sqrt{9} = 3$

Example C

Consider the equation $(x + 3)^{2} + (y + 5)^{2} = 16$ :

$(x + 3)^{2} + (y + 5)^{2} = 16$

The center $(h, k)$ is $(- 3, - 5)$ , and the radius $r$ is:

$r = \sqrt{16} = 4$

Example D

Consider the equation $(x - 8)^{2} + (y + 6)^{2} = 49$ :

$(x - 8)^{2} + (y + 6)^{2} = 49$

The center $(h, k)$ is $(8, - 6)$ , and the radius $r$ is:

$r = \sqrt{49} = 7$

Example E

Consider the equation $x^{2} + (y + 4)^{2} = 4$ :

$x^{2} + (y + 4)^{2} = 4$

The center $(h, k)$ is $(0, - 4)$ , and the radius $r$ is:

$r = \sqrt{4} = 2$

Example F

Consider the equation $(x + 6)^{2} + y^{2} = 64$ :

$(x + 6)^{2} + y^{2} = 64$

The center $(h, k)$ is $(- 6, 0)$ , and the radius $r$ is:

$r = \sqrt{64} = 8$

Completed Table

The following table summarizes the centers and radii of the circles from the examples:

$\begin{array}{ccc} Equation of Circle & Center (h, k) & Radius \\ x^{2} + y^{2} = 25 & (0, 0) & 5 \\ (x - 2)^{2} + (y - 1)^{2} = 9 & (2, 1) & 3 \\ (x + 3)^{2} + (y + 5)^{2} = 16 & (- 3, - 5) & 4 \\ (x - 8)^{2} + (y + 6)^{2} = 49 & (8, - 6) & 7 \\ x^{2} + (y + 4)^{2} = 4 & (0, - 4) & 2 \\ (x + 6)^{2} + y^{2} = 64 & (- 6, 0) & 8 \end{array}$

Conclusion

By examining the structure of the circle's equation, students can easily identify its center $(h, k)$ and radius $r$ . The square of the radius is always the constant on the right side of the equation, and the center coordinates come from the terms inside the parentheses in the form $(x - h)^{2} + (y - k)^{2}$ .

Equation of a circle passing through two points

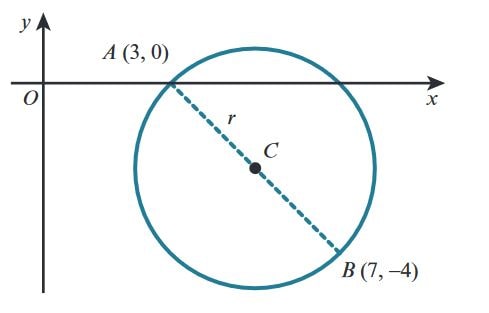
A is the point $A (3, 0)$ and B is the point $B (7, - 4)$ .

Find the equation of the circle that has $A B$ as a diameter.

Answer

The centre of the circle, $C$ , is the midpoint of $A B$ .

$C = (\frac{3 + 7}{2}, \frac{0 + (- 4)}{2}) = (5, - 2)$

Radius of the circle, $r$ , is equal to $A C$ .

$r = \sqrt{(5 - 3)^{2} + (- 2 - 0)^{2}} = \sqrt{8}$

Equation of the circle is $(x - a)^{2} + (y - b)^{2} = r^{2}$ , where $a = 5$ , $b = - 2$ , and $r = \sqrt{8}$ .

$(x - 5)^{2} + (y + 2)^{2} = {(\sqrt{8})}^{2}$

Therefore, the equation of the circle is:

$(x - 5)^{2} + (y + 2)^{2} = 8$

General Equation of a circle

Find the centre and the radius of the circle $x^{2} + y^{2} + 10 x - 8 y - 40 = 0$ .

Answer

We answer this question by first completing the square.

$x^{2} + 10 x + y^{2} - 8 y - 40 = 0$

Complete the square for both $x$ and $y$ :

$(x + 5)^{2} - 5^{2} + (y - 4)^{2} - 4^{2} - 40 = 0$

Collect the constant terms together:

$(x + 5)^{2} + (y - 4)^{2} = 81$

Now, compare with the equation $(x - a)^{2} + (y - b)^{2} = r^{2}$ :

$a = - 5, b = 4, r^{2} = 81$

The center is $(- 5, 4)$ and the radius is $r = 9$ .

Important points to Remember

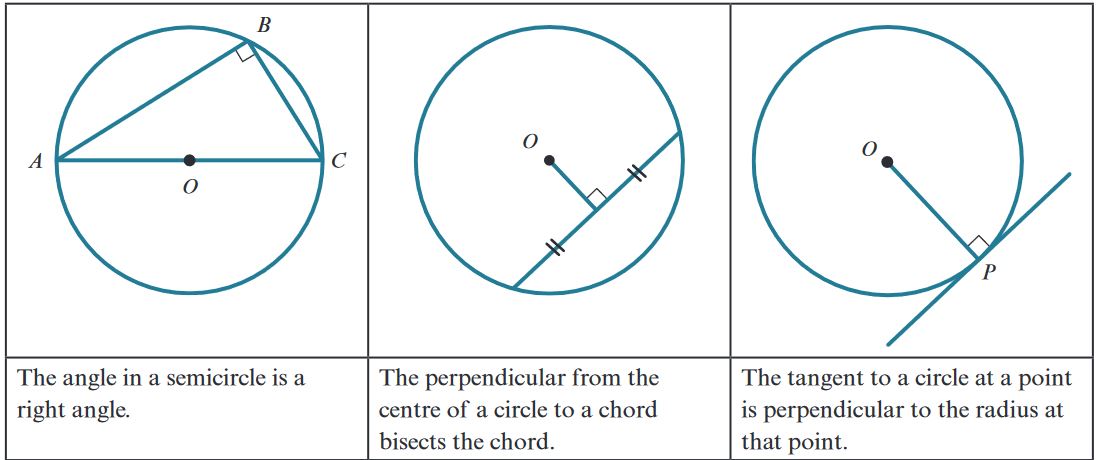
The Angle in a Semicircle is a Right Angle

Note: The angle formed at the circumference by a diameter of the circle is always a right angle (90 degrees).

Example Problem 1

Problem: In a circle with center $O$ , the diameter $A C$ is drawn. A point $B$ is placed on the circumference such that $A B$ and $B C$ are chords. Find the angle $∠ A B C$ .

Solution:

Since $A C$ is a diameter, the angle $∠ A B C$ is a right angle.

$∠ A B C = 90^{\circ}$

Example Problem 2

Problem: In a circle with center $O$ , the diameter $P Q$ is drawn. If a point $R$ lies on the circumference such that $P R$ and $R Q$ form a triangle, find the measure of $∠ P R Q$ .

Solution:

Since $P Q$ is the diameter of the circle, the angle subtended by it on the circumference is always a right angle.

$∠ P R Q = 90^{\circ}$

The Perpendicular from the Center of a Circle to a Chord Bisects the Chord

Note: The perpendicular dropped from the center of a circle to any chord will always bisect the chord.

Example Problem 1

Problem: In a circle with center $O$ , a chord $A B$ is 10 cm long. The perpendicular from the center $O$ to the chord $A B$ intersects $A B$ at point $M$ . Find the length of $A M$ .

Solution:

Since the perpendicular from the center of the circle bisects the chord, $A M = M B$ . Therefore, the length of $A M$ is half the length of the chord:

$A M = \frac{10}{2} = 5 cm$

Example Problem 2

Problem: In a circle with center $O$ , a chord $C D$ is 16 cm long. The perpendicular from the center $O$ to the chord intersects $C D$ at point $N$ . Find the lengths of $C N$ and $N D$ .

Solution:

The perpendicular from the center bisects the chord $C D$ , so $C N = N D$ . Thus, each segment of the chord is:

$C N = N D = \frac{16}{2} = 8 cm$

The Tangent to a Circle at a Point is Perpendicular to the Radius at that Point

Note: The tangent line to a circle at any point on the circle is perpendicular to the radius drawn to the point of tangency.

Example Problem 1

Problem: In a circle with center $O$ , the radius $O P$ is drawn to the point of tangency $P$ , where the line $T P$ touches the circle. If $T P$ is the tangent line, find the measure of the angle between $O P$ and $T P$ .

Solution:

By the property of tangents, the angle between the radius and the tangent at the point of tangency is 90 degrees. Therefore,

$∠ O P T = 90^{\circ}$

Example Problem 2

Problem: A circle with center $O$ has a tangent line $Q R$ touching the circle at point $R$ . The radius $O R$ is drawn to the point $R$ . What is the angle between $O R$ and $Q R$ ?

Solution:

The radius $O R$ is perpendicular to the tangent $Q R$ at the point of tangency $R$ . Therefore, the angle between them is 90 degrees.

$∠ O R Q = 90^{\circ}$

1. Find the center and the radius of each of the following circles:

(a) $x^{2} + y^{2} = 16$

Solution: $The equation of the circle is in the form x^{2} + y^{2} = r^{2} .$ $∴ Center = (0, 0) and Radius = \sqrt{16} = 4$

(b) $2 x^{2} + 2 y^{2} = 9$

Solution: $\frac{2 x^{2} + 2 y^{2}}{2} = \frac{9}{2}$ $∴ x^{2} + y^{2} = \frac{9}{2}$ $∴ Center = (0, 0) and Radius = \sqrt{\frac{9}{2}}$

(c) $x^{2} + (y - 2)^{2} = 25$

Solution: $∴ Center = (0, 2) and Radius = \sqrt{25} = 5$

(d) $(x - 5)^{2} + (y + 3)^{2} = 4$

Solution: $∴ Center = (5, - 3) and Radius = \sqrt{4} = 2$

(e) $(x + 7)^{2} + y^{2} = 18$

Solution: $∴ Center = (- 7, 0) and Radius = \sqrt{18}$

(f) $2 (x - 3)^{2} + 2 (y + 4)^{2} = 45$

Solution: $\frac{2 (x - 3)^{2} + 2 (y + 4)^{2}}{2} = \frac{45}{2}$ $∴ Center = (3, - 4) and Radius = \sqrt{\frac{45}{2}}$

(g) $x^{2} + y^{2} - 8 x + 20 y + 110 = 0$

Solution: $x^{2} - 8 x + y^{2} + 20 y = - 110$ $(x - 4)^{2} + (y + 10)^{2} = 6$ $∴ Center = (4, - 10) and Radius = \sqrt{6}$

(h) $2 x^{2} + 2 y^{2} - 14 x - 10 y - 163 = 0$

Solution: $x^{2} - 7 x + y^{2} - 5 y = \frac{163}{2}$ $∴ Center = (\frac{7}{2}, \frac{5}{2})$

2. Find the equation of each of the following circles:

(a) Center $(0, 0)$ , Radius 8

Solution: $∴ x^{2} + y^{2} = 64$

(b) Center $(5, - 2)$ , Radius 4

Solution: $∴ (x - 5)^{2} + (y + 2)^{2} = 16$

(c) Center $(- 1, 3)$ , Radius $\sqrt{7}$

Solution: $∴ (x + 1)^{2} + (y - 3)^{2} = 7$

(d) Center $(\frac{1}{2}, - \frac{3}{2})$ , Radius $\frac{5}{2}$

Solution: ${(x - \frac{1}{2})}^{2} + {(y + \frac{3}{2})}^{2} = \frac{25}{4}$

3. Find the equation of the circle with center (2, 5) passing through the point (6, 8).

Solution: $r = \sqrt{(6 - 2)^{2} + (8 - 5)^{2}} = 5$ $∴ (x - 2)^{2} + (y - 5)^{2} = 25$

4. A diameter of a circle has its endpoints at A(-6, 8) and B(2, -4). Find the equation of the circle.

Solution: $Midpoint = (- 2, 2)$ $r = \frac{\sqrt{208}}{2} = \sqrt{52}$ $∴ (x + 2)^{2} + (y - 2)^{2} = 52$

Question

Find the equation of the line with gradient -4, and passing thru P(5m, 3m) intersects the x-Axis at A, and y-axis at B

(i) Find the equation of the line

(ii) Find the area of the triangle AOB

(iii) Find the general form of the equation of a line

(iv) The line thru P perpendicular to AB intersects the x-axis at C, Check if the midpoint of PC lies on the line y = x

$y - y_{1} = m (x - x_{1})$

Where:

$m$ is the gradient of the line.
$(x_{1}, y_{1})$ is a point on the line.

Given:

Gradient $m = - 4$
Point $P (5 m, 3 m)$

Substitute these values into the equation of the line:

$y - 3 m = - 4 (x - 5 m)$

Simplifying:

$y - 3 m = - 4 x + 20 m$

$y = - 4 x + 23 m$

Thus, the equation of the line is:

$y = - 4 x + 23 m$

(ii) The coordinates of point $A$ (x-intercept) are:

$A (\frac{23 m}{4}, 0)$

The coordinates of point $B$ (y-intercept) are:

$B (0, 23 m)$

Finding the Area of Triangle $A O B$

The area of triangle $A O B$ is given by:

$Area = \frac{1}{2} \times base \times height$

Using the coordinates of $A (\frac{23 m}{4}, 0)$ and $B (0, 23 m)$ , we get:

$Area = \frac{1}{2} \times \frac{23 m}{4} \times 23 m$

Simplifying this, we find:

$Area = \frac{529 m^{2}}{8}$

Thus, the area of triangle $A O B$ is:

$\frac{529 m^{2}}{8}$

(iii) The equation of the line perpendicular to $A B$ , passing through $P (5 m, 3 m)$ , is:

$y = \frac{1}{4} x + \frac{7 m}{4}$

(iv) The coordinates of point $C$ (x-intercept of the perpendicular line) are:

$C (- 7 m, 0)$

(v) The midpoint of $P C$ is:

$M = (- m, \frac{3 m}{2})$

Since $y = \frac{3 m}{2} \neq - m$ , the midpoint does not lie on the line $y = x$ .

Question

Find the equation of the line with gradient -2, and passing thru P(3t, 2t) and intersects the x-Axis at A, and y-axis at B

(i) Find the area of the triangle AOB in terms of t

The line thru P, perpendicular to AB, intersects the x-axis at C

(ii) Show that the midpoint of PC lies on y = x

Solution

1.

Solution: The equation of the line with gradient $- 2$ passing through the point $P (3 t, 2 t)$ is given by:

y - 2 t = - 2 (x - 3 t)

Simplifying this equation:

y = - 2 x + 8 t

The line intersects the x-axis at $A (4 t, 0)$ and the y-axis at $B (0, 8 t)$ . The area of triangle $A O B$ is given by:

Area = \frac{1}{2} \times 4 t \times 8 t = 16 t^{2}

Therefore, the area of triangle $A O B$ is = $16 t^{2}$ .

2.

Solution: The equation of the line through $P (3 t, 2 t)$ perpendicular to $A B$ has a gradient of $\frac{1}{2}$ . The equation of this line is:

y - 2 t = \frac{1}{2} (x - 3 t)

Simplifying:

y = \frac{1}{2} x + \frac{t}{2}

This line intersects the x-axis at $C (- t, 0)$ . The midpoint of $P C$ is:

Midpoint = (\frac{2 t}{2}, \frac{2 t}{2}) = (t, t)

Since the midpoint is $(t, t)$ , it lies on the line $y = x$ .

Question

Problem:

The diagram shows the graph of $y = f (x)$ , where $f (x) = \frac{5}{2} \cos (3 x) + 1$ for $0 \leq x \leq \frac{π}{3}$ .

(a) State the range of $f (x)$ .

Solution:

Step 1: Analyze the function $f (x)$

We are given the function:

$f (x) = \frac{5}{2} \cos (3 x) + 1$

The cosine function $\cos (3 x)$ has a range of:

$- 1 \leq \cos (3 x) \leq 1$

Step 2: Apply the transformations

Scaling by $\frac{5}{2}$ gives the range:

$- \frac{5}{2} \leq \frac{5}{2} \cos (3 x) \leq \frac{5}{2}$

Adding $1$ shifts the range:

$- \frac{5}{2} + 1 \leq f (x) \leq \frac{5}{2} + 1$

Step 3: Simplify the range

The final range becomes:

$- \frac{3}{2} \leq f (x) \leq \frac{7}{2}$

Thus, the range of $f (x)$ is:

$[- \frac{3}{2}, \frac{7}{2}]$

Solution for Question (b):

The value of $k$ is:

$k = 1$

This means there is no vertical scaling applied to the function $f (x)$ .

The transformation is an identity transformation, meaning the curve remains unchanged under this mapping.

Solution for Question (c):

The equation of the curve reflected in the x-axis is given by:

$y = - f (x) = - (\frac{5}{2} \cos (3 x) + 1)$

Simplifying this gives:

$y = - \frac{5}{2} \cos (3 x) - 1$

Thus, the equation in the form $y = a \cos (2 x) + b$ is:

$a = - \frac{5}{2}, b = - 1$

Problem:

The diagram shows the graph of $y = f (x)$ , where $f (x) = \frac{5}{2} \cos (2 x) + \frac{1}{2}$ for $0 \leq x \leq π$ .

(a) State the range of $f (x)$ .

Solution:

Step 1: Analyze the function $f (x)$

We are given the function:

$f (x) = \frac{5}{2} \cos (2 x) + \frac{1}{2}$

The cosine function $\cos (2 x)$ has a range of:

$- 1 \leq \cos (2 x) \leq 1$

Step 2: Apply the transformations

Scaling by $\frac{5}{2}$ gives the range:

$- \frac{5}{2} \leq \frac{5}{2} \cos (2 x) \leq \frac{5}{2}$

Adding $\frac{1}{2}$ shifts the range:

$- \frac{5}{2} + \frac{1}{2} \leq f (x) \leq \frac{5}{2} + \frac{1}{2}$

Step 3: Simplify the range

The final range becomes:

$- 2 \leq f (x) \leq 3$

Thus, the range of $f (x)$ is:

$[- 2, 3]$

Question

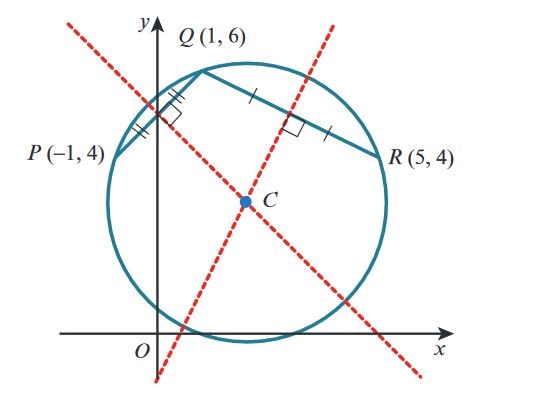
Solution for the Equation of a Circle:

A circle passes through the points $P (- 1, 4)$ , $Q (1, 6)$ , and $R (5, 4)$ .

Find the equation of the circle.

Step 1: Find the Midpoint of $P Q$ and the Perpendicular Bisector

The midpoint of $P Q$ is:

$Midpoint of P Q = (\frac{- 1 + 1}{2}, \frac{4 + 6}{2}) = (0, 5)$

The gradient of $P Q$ is:

$Gradient of P Q = \frac{6 - 4}{1 - (- 1)} = 1$

The gradient of the perpendicular bisector of $P Q$ is the negative reciprocal, so:

$Gradient of perpendicular bisector of P Q = - 1$

The equation of the perpendicular bisector of $P Q$ is:

$(y - 5) = - 1 (x - 0)$

$y = - x + 5 (Equation 1)$

Step 2: Find the Midpoint of $Q R$ and the Perpendicular Bisector

The midpoint of $Q R$ is:

$Midpoint of Q R = (\frac{1 + 5}{2}, \frac{6 + 4}{2}) = (3, 5)$

The gradient of $Q R$ is:

$Gradient of Q R = \frac{4 - 6}{5 - 1} = - \frac{1}{2}$

The gradient of the perpendicular bisector of $Q R$ is the negative reciprocal, so:

$Gradient of perpendicular bisector of Q R = 2$

The equation of the perpendicular bisector of $Q R$ is:

$(y - 5) = 2 (x - 3)$

$y = 2 x - 1 (Equation 2)$

Step 3: Solve the Two Equations to Find the Centre of the Circle

Solving equations (1) and (2) gives:

$x = 2, y = 3$

The centre of the circle is $(2, 3)$ .

Step 4: Find the Radius of the Circle

The radius is the distance from the centre $(2, 3)$ to any of the points, say $R (5, 4)$ . Using the distance formula:

$Radius = C R = \sqrt{(5 - 2)^{2} + (4 - 3)^{2}} = \sqrt{9 + 1} = \sqrt{10}$

Step 5: Equation of the Circle

The equation of the circle is:

$(x - 2)^{2} + (y - 3)^{2} = 10$

Question:

Find the equation of the circle with center(2,5) passing thru the point (6,8)

Solution

The general equation of a circle with center

(h, k)

and radius

r

is given by:

(x - h)^{2} + (y - k)^{2} = r^{2}

Here, the center is $(2, 5)$ . Substituting $h = 2$ and $k = 5$ into the equation, we get:

(x - 2)^{2} + (y - 5)^{2} = r^{2}

We are also given that the circle passes through the point $(6, 8)$ . Substituting $x = 6$ and $y = 8$ into the equation to find $r^{2}$ :

(6 - 2)^{2} + (8 - 5)^{2} = r^{2}

4^{2} + 3^{2} = r^{2}

16 + 9 = r^{2}

r^{2} = 25

Therefore, the equation of the circle is:

(x - 2)^{2} + (y - 5)^{2} = 25

Hence, the equation of the circle is $(x - 2)^{2} + (y - 5)^{2} = 25$ .

Question

Solution

We are given:

f (x) = \frac{1}{2} x - a, g (x) = 3 x + b

and the conditions:

g g (2) = 10, f^{- 1} (2) = 14

Part (a): Solving for $a$ and $b$

We start with $g g (2) = 10$ . First, compute $g (g (2))$ :

g (2) = 3 (2) + b = 6 + b

Substitute into $g (g (2))$ :

g (g (2)) = g (6 + b) = 3 (6 + b) + b = 18 + 3 b + b = 18 + 4 b

Since $g (g (2)) = 10$ , we have:

18 + 4 b = 10 ⟹ 4 b = - 8 ⟹ b = - 2

Next, use $f^{- 1} (2) = 14$ . By definition of the inverse function, we know:

f (14) = 2

Substitute into $f (x)$ :

f (14) = \frac{1}{2} (14) - a = 7 - a

Since $f (14) = 2$ , we have:

7 - a = 2 ⟹ a = 5

Part (b): Find $g f (x)$

Using $a = 5$ and $b = - 2$ , we have $f (x) = \frac{1}{2} x - 5$ and $g (x) = 3 x - 2$ . Now, calculate $g (f (x))$ :

g (f (x)) = g (\frac{1}{2} x - 5) = 3 (\frac{1}{2} x - 5) - 2

Simplifying:

g (f (x)) = 3 (\frac{1}{2} x - 5) - 2 = \frac{3}{2} x - 15 - 2 = \frac{3}{2} x - 17

Therefore, $g f (x) = \frac{3}{2} x - 17$ .

Exploring Unique and Thought-Provoking Knowledge

This section explores questions from various fields that provide deep insights and an intellectual edge.

Worked Examples

Q1

What was the primary reason for the collapse of the Bronze Age civilizations around 1200 BCE?

Solution:

The collapse is attributed to a combination of factors, including natural disasters, invasions by the Sea Peoples, internal social upheavals, and a breakdown in trade networks.
This disrupted the supply of tin and copper necessary for making bronze, leading to the downfall of major civilizations such as the Mycenaeans, Hittites, and Egyptians.

Q2

What is the "Ship of Theseus" paradox, and what does it question about identity?

Solution:

The "Ship of Theseus" paradox asks whether a ship that has had all its components replaced remains fundamentally the same ship.
This paradox challenges the concept of identity, questioning whether an object that undergoes gradual change can still be considered the same object.

Q3

What is Gödel's Incompleteness Theorem, and how does it impact mathematical systems?

Solution:

Gödel's Incompleteness Theorem states that in any consistent mathematical system, there are statements that are true but cannot be proven within that system.
This means that no mathematical system can be both complete and consistent, implying that some truths will always lie beyond formal proof.

Q4

What is the "Fermi Paradox," and what does it question about extraterrestrial life?

Solution:

The Fermi Paradox questions why, despite the high probability of extraterrestrial life, we have not yet encountered any evidence of other civilizations.
This paradox highlights the apparent contradiction between the vastness of the universe and the lack of observational evidence of alien life.

Q5

What is the Sapir-Whorf Hypothesis, and how does it influence our understanding of language and thought?

Solution:

The Sapir-Whorf Hypothesis posits that the structure of a language influences its speakers' cognition and worldview.
It suggests that people who speak different languages perceive and think about the world differently because language shapes thought processes.

Q6

What is the "Red Queen Hypothesis," and how does it relate to evolutionary biology?

Solution:

The Red Queen Hypothesis suggests that organisms must constantly adapt and evolve to survive in an ever-changing environment where other species are also evolving.
This concept emphasizes continuous evolutionary arms races between species.

Q7

What is the significance of Göbekli Tepe, and how does it challenge traditional views of human civilization?

Solution:

Göbekli Tepe is significant because it predates the advent of agriculture and permanent settlements.
This challenges the traditional view that complex societies developed only after the establishment of agriculture and suggests that organized religion and monumental architecture may have preceded farming.

Q8

What is the "Dunning-Kruger Effect," and how does it influence people's perception of their abilities?

Solution:

The Dunning-Kruger Effect is a cognitive bias in which people with low ability or knowledge overestimate their competence, while those with high competence tend to underestimate their abilities.
This effect highlights the lack of self-awareness in individuals regarding their own skills.

Q9

What is the "Paradox of Thrift," and how does it relate to macroeconomic theory?

Solution:

The Paradox of Thrift suggests that while saving money is beneficial for individuals, if everyone saves more during a recession, overall demand will fall, leading to lower total savings and a weaker economy.
This paradox illustrates the conflict between individual rationality and collective outcomes in economics.

Q10

What is the significance of the "Arnolfini Portrait" by Jan van Eyck, and what are its key symbolic elements?

Solution:

The "Arnolfini Portrait" is significant for its intricate detail and use of symbolism.
Key elements include the mirror reflecting the scene, the dog symbolizing loyalty, and the use of light to create depth and realism, often interpreted as a visual contract or depiction of marriage.

Algebra Week 5 Teaching Plan

Worked Examples

Q1 (Find the Vertex and Axis of Symmetry for $f (x) = x^{2} + 8 x - 1$ )

Given: $f (x) = x^{2} + 8 x - 1$

Solution:

Complete the square: $f (x) = x^{2} + 8 x + {(\frac{8}{2})}^{2} - {(\frac{8}{2})}^{2} - 1 = (x + 4)^{2} - 17$
The vertex is $(- 4, - 17)$ .
The formula for the axis of symmetry is $x = - \frac{b}{2 a}$ . For this equation, $a = 1$ and $b = 8$ , so: $x = - \frac{8}{2 (1)} = - 4$
The axis of symmetry is $x = - 4$ .

Q2 (Find the Vertex and Axis of Symmetry for $f (x) = x^{2} + 10 x + 25$ )

Given: $f (x) = x^{2} + 10 x + 25$

Solution:

Recognize that this is a perfect square: $f (x) = (x + 5)^{2}$
The vertex is $(- 5, 0)$ .
Using the formula for the axis of symmetry, $x = - \frac{b}{2 a}$ , with $a = 1$ and $b = 10$ : $x = - \frac{10}{2 (1)} = - 5$
The axis of symmetry is $x = - 5$ .

Q3 (Find the Vertex and Axis of Symmetry for $f (x) = - x^{2} + 2 x + 5$ )

Given: $f (x) = - x^{2} + 2 x + 5$

Solution:

Factor out the negative sign and complete the square: $f (x) = - (x^{2} - 2 x + 1 - 1 + 5) = - (x - 1)^{2} + 6$
The vertex is $(1, 6)$ .
Using the formula for the axis of symmetry, $x = - \frac{b}{2 a}$ , with $a = - 1$ and $b = 2$ : $x = - \frac{2}{2 (- 1)} = 1$
The axis of symmetry is $x = 1$ .

Q4 (Find the Vertex and Axis of Symmetry for $f (x) = - 2 x^{2} - 8 x - 3$ )

Given: $f (x) = - 2 x^{2} - 8 x - 3$

Solution:

Factor out the -2 and complete the square: $f (x) = - 2 (x^{2} + 4 x + 4 - 4 - \frac{3}{2}) = - 2 (x + 2)^{2} + 5$
The vertex is $(- 2, 5)$ .
Using the formula for the axis of symmetry, $x = - \frac{b}{2 a}$ , with $a = - 2$ and $b = - 8$ : $x = - \frac{- 8}{2 (- 2)} = - 2$
The axis of symmetry is $x = - 2$ .

Q5 (Find the Vertex and Axis of Symmetry for $y = - x^{2} + 10 x - 34$ )

Given: $y = - x^{2} + 10 x - 34$

Solution:

Complete the square: $y = - (x^{2} - 10 x + 25 - 25 - 34) = - (x - 5)^{2} - 9$
The vertex is $(5, - 9)$ .
Using the formula for the axis of symmetry, $x = - \frac{b}{2 a}$ , with $a = - 1$ and $b = 10$ : $x = - \frac{10}{2 (- 1)} = 5$
The axis of symmetry is $x = 5$ .

Q6 (Find the Vertex and Axis of Symmetry for $y = - x^{2} - 6 x + 1$ )

Given: $y = - x^{2} - 6 x + 1$

Solution:

Complete the square: $y = - (x^{2} + 6 x + 9 - 9 + 1) = - (x + 3)^{2} + 10$
The vertex is $(- 3, 10)$ .
Using the formula for the axis of symmetry, $x = - \frac{b}{2 a}$ , with $a = - 1$ and $b = - 6$ : $x = - \frac{- 6}{2 (- 1)} = - 3$
The axis of symmetry is $x = - 3$ .

Q7 (Find the Vertex and Axis of Symmetry for $y = - 4 x^{2} + 12 x - 7$ )

Given: $y = - 4 x^{2} + 12 x - 7$

Solution:

Factor out the -4 and complete the square: $y = - 4 (x^{2} - 3 x + \frac{9}{4} - \frac{9}{4} - 7) = - 4 (x - \frac{3}{2})^{2} + 2$
The vertex is $(\frac{3}{2}, 2)$ .
Using the formula for the axis of symmetry, $x = - \frac{b}{2 a}$ , with $a = - 4$ and $b = 12$ : $x = - \frac{12}{2 (- 4)} = \frac{3}{2}$
The axis of symmetry is $x = \frac{3}{2}$ .

Q8: Find the Vertex and Axis of Symmetry for $y = - 9 x^{2} + 6 x + 2$

Given: $y = - 9 x^{2} + 6 x + 2$

Solution:

Factor out the -9 and complete the square: $y = - 9 (x^{2} - \frac{2}{3} x + \frac{1}{9} - \frac{1}{9} + 2) = - 9 (x - \frac{1}{3})^{2} + 3$
The vertex is $(\frac{1}{3}, 3)$ .
Using the formula for the axis of symmetry, $x = - \frac{b}{2 a}$ , with $a = - 9$ and $b = 6$ : $x = - \frac{6}{2 (- 9)} = \frac{1}{3}$
The axis of symmetry is $x = \frac{1}{3}$ .

Q9: Find the Vertex and Axis of Symmetry for $y = 4 x^{2} - 1$

Given: $y = 4 x^{2} - 1$

Solution:

This is already a perfect square form: $y = 4 (x)^{2} - 1$
The vertex is $(0, - 1)$ .
Using the formula for the axis of symmetry, $x = - \frac{b}{2 a}$ , with $a = 4$ and $b = 0$ : $x = 0$
The axis of symmetry is $x = 0$ .

Q10: Find the Vertex and Axis of Symmetry for $y = x^{2} - 16$

Given: $y = x^{2} - 16$

Solution:

This is already a perfect square form: $y = (x)^{2} - 16$
The vertex is $(0, - 16)$ .
Using the formula for the axis of symmetry, $x = - \frac{b}{2 a}$ , with $a = 1$ and $b = 0$ : $x = 0$
The axis of symmetry is $x = 0$ .

Quadratic Equations-finding a and b

Worked Examples

Q1 (Write $y = 4 x^{2} + 8 x - 5$ in the form $y = a (x + b)^{2} + c$ , where $a$ , $b$ , and $c$ are integers)

Given: $y = 4 x^{2} + 8 x - 5$

Solution:

First, factor out the coefficient of $x^{2}$ from the first two terms: $y = 4 (x^{2} + 2 x) - 5$
Now complete the square by adding and subtracting the square of half the coefficient of $x$ . Half of 2 is 1, and $1^{2} = 1$ : $y = 4 (x^{2} + 2 x + 1 - 1) - 5$
Simplify the expression: $y = 4 ((x + 1)^{2} - 1) - 5$
Distribute the 4: $y = 4 (x + 1)^{2} - 4 - 5$
Combine the constants: $y = 4 (x + 1)^{2} - 9$
Thus, the quadratic function in the form $y = a (x + b)^{2} + c$ is: $y = 4 (x + 1)^{2} - 9$ where $a = 4$ , $b = 1$ , and $c = - 9$ .

Intersection of a Quadratic Curve and a Line

Q2 (Find any points of intersection between the curve $C$ and the line $l$ )

Given:

Curve $C$ has the equation $y = x^{2} - 3 x + 2$ .
Line $l$ has the equation $y = 3 x - 7$ .

Solution:

To find the points of intersection, set the equations for the curve and the line equal to each other: $x^{2} - 3 x + 2 = 3 x - 7$
Rearrange the equation to form a standard quadratic equation: $x^{2} - 3 x - 3 x + 2 + 7 = 0 ⟹ x^{2} - 6 x + 9 = 0$
Factor the quadratic equation: $(x - 3)^{2} = 0$
Solving for $x$ , we get: $x = 3$
Substitute $x = 3$ back into the equation of the line to find the corresponding value of $y$ : $y = 3 (3) - 7 = 9 - 7 = 2$
Therefore, the point of intersection is $(3, 2)$ .

Quadratic Equations-Conditions for No Real Roots

Worked Examples

Q1: Show that $p^{2} < 12 q$ for the equation $y = 3 x^{2} + 2 p x + 4 q$ having no real roots

Given: $y = 3 x^{2} + 2 p x + 4 q$

Solution:

The general condition for a quadratic equation to have no real roots is that the discriminant must be less than zero. The discriminant $Δ$ of a quadratic equation $a x^{2} + b x + c = 0$ is given by: $Δ = b^{2} - 4 a c$
For the given equation $y = 3 x^{2} + 2 p x + 4 q$ , the coefficients are: $a = 3, b = 2 p, c = 4 q$
Substituting these values into the discriminant formula: $Δ = (2 p)^{2} - 4 (3) (4 q) = 4 p^{2} - 48 q$
For the equation to have no real roots, the discriminant must be less than zero: $4 p^{2} - 48 q < 0$
Simplifying the inequality: $4 p^{2} < 48 q$ Dividing both sides by 4: $p^{2} < 12 q$
Thus, we have shown that $p^{2} < 12 q$ .

Q2: Find the minimum value of the function $f (x) = x^{2} + 4 x + c$ , giving your answer in terms of $c$

Given: $f (x) = x^{2} + 4 x + c$

Solution:

To find the minimum value of the function, we complete the square.
First, factor the quadratic and linear terms: $f (x) = (x^{2} + 4 x) + c$
Complete the square by adding and subtracting the square of half the coefficient of $x$ . Half of 4 is 2, and $2^{2} = 4$ : $f (x) = (x^{2} + 4 x + 4 - 4) + c = (x + 2)^{2} - 4 + c$
The minimum value of $(x + 2)^{2}$ occurs when $(x + 2)^{2} = 0$ . Therefore, the minimum value of the function is: $f (x) = - 4 + c$
Thus, the minimum value of the function is $c - 4$ , and it occurs when $x = - 2$ .

Q3: Sketch the graph of $y = 12 x^{2} - 5 x - 72$ , labelling any points where the graph crosses the coordinate axes and the turning point

Given: $y = 12 x^{2} - 5 x - 72$

Solution:

To sketch the graph, we need to find:
- The x-intercepts (roots of the quadratic)
- The y-intercept (value of $y$ when $x = 0$ )
- The turning point (vertex of the parabola)

Step 1: Find the x-intercepts

To find the x-intercepts, set $y = 0$ and solve the quadratic equation: $12 x^{2} - 5 x - 72 = 0$
We can use the quadratic formula: $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ where $a = 12$ , $b = - 5$ , and $c = - 72$ .
Substituting the values: $x = \frac{- (- 5) \pm \sqrt{(- 5)^{2} - 4 (12) (- 72)}}{2 (12)} = \frac{5 \pm \sqrt{25 + 3456}}{24} = \frac{5 \pm \sqrt{3481}}{24} = \frac{5 \pm 59}{24}$
This gives two solutions: $x = \frac{5 + 59}{24} = \frac{64}{24} = \frac{8}{3}, x = \frac{5 - 59}{24} = \frac{- 54}{24} = - \frac{9}{4}$
Therefore, the x-intercepts are $x = \frac{8}{3}$ and $x = - \frac{9}{4}$ .

Step 2: Find the y-intercept

To find the y-intercept, set $x = 0$ : $y = 12 (0)^{2} - 5 (0) - 72 = - 72$
The y-intercept is $y = - 72$ .

Step 3: Find the turning point

We can find the turning point using the formula for the vertex $x = - \frac{b}{2 a}$ . For the given equation, $a = 12$ and $b = - 5$ : $x = - \frac{- 5}{2 (12)} = \frac{5}{24}$
Substitute $x = \frac{5}{24}$ into the equation to find the corresponding $y$ -value: $y = 12 {(\frac{5}{24})}^{2} - 5 (\frac{5}{24}) - 72$ Simplifying this will give the value of $y$ at the turning point.