Transformations

Introduction to Transformations:

A transformation is a change made to a figure or graph, such as moving it up or down, left or right, or flipping it over. Transformations are an important concept in geometry and algebra because they help us understand how shapes and graphs can change while still keeping their fundamental properties.

Types of Transformations:

1. Translation: This is when a shape or graph is moved in a straight line from one place to another without changing its shape, size, or orientation.

- **Horizontal Translation:** Moving left or right.

- **Vertical Translation:** Moving up or down.

2. Reflection: This is when a shape or graph is flipped over a line, creating a mirror image. Common lines of reflection include the x-axis and y-axis.

3. Rotation: This is when a shape or graph is turned around a point. The shape stays the same size and shape but is in a different orientation.

4. Dilation (Scaling): This is when a shape or graph is made larger or smaller. The shape stays the same, but its size changes.

Detailed Explanation of Translation:

Translation is one of the simplest transformations. It involves sliding a figure or graph along the x-axis, y-axis, or both without changing its shape, size, or orientation. When translating a figure or graph, every point of the figure moves the same distance in the same direction.

Example Problem:

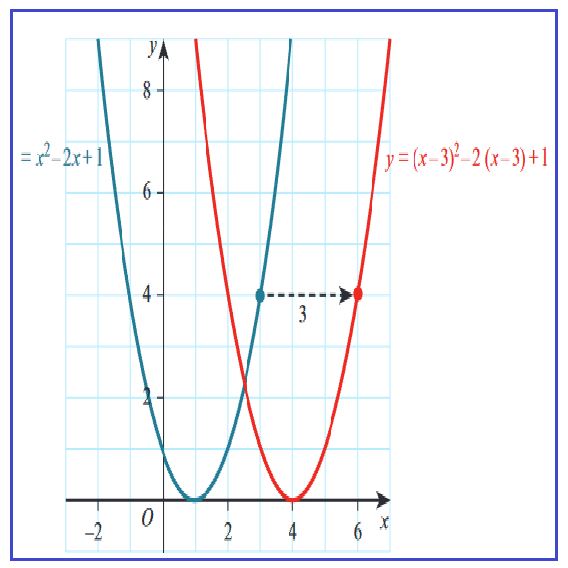
Consider the graphs of two functions:

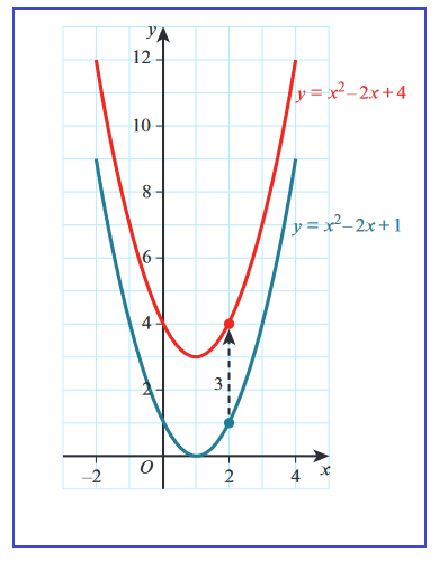
Notice that these two equations are very similar. The only difference is the constant term (the number without an \(x\) next to it). The first equation has \(+1\), and the second has \(+4\).

Understanding the Translation:

When you look at the graphs of these two equations, you can see that they have the same shape. The red graph is the same as the blue graph, but it is shifted up by 3 units.

To understand why this happens, consider what happens to the \(y\)-coordinates. For any value of \(x\), the \(y\)-coordinate of the red graph is 3 units higher than the \(y\)-coordinate of the blue graph. This means that the red graph is a translation of the blue graph, moved up by 3 units.

Translation by a Vector:

In mathematics, we can describe this translation using a vector. A vector tells us how far and in what direction to move every point on the graph. For this translation, the vector is:

This vector means "move every point up by 3 units and don't move it left or right."

Final Explanation:

So, the graph of \(y = x^2 - 2x + 4\) is simply the graph of \(y = x^2 - 2x + 1\) translated up by 3 units.

Visual Representation:

Consider the graph to better understand the translation:

Here, the blue graph represents \(y = x^2 - 2x + 1\), and the red graph represents \(y = x^2 - 2x + 4\). The vertical distance between corresponding points on the two graphs is 3 units.

Key Points to Remember:

• Translation does not change the shape or orientation of the graph, only its position.
• Vertical translations move the graph up or down, while horizontal translations move it left or right.
• The vector used in translation shows the direction and distance of the movement.

The graph of the function moves up by \( c \) units if \( c > 0 \) or down by \( c < 0 \).

Compare the constant term in the function. If a constant is added or subtracted, this results in a vertical translation.

The graph of the function moves right by \( h \) units if \( h > 0 \) or left by \( h < 0 \).

Look for a change inside the argument of the function (i.e., inside the parentheses with \( x \)). If \( x \) is replaced by \( x - h \), it shifts the graph horizontally.

Step-by-Step Explanation:

Now consider the two functions:

We obtain the second function by replacing \( x \) with \( x - 3 \) in the first function.

Let's break this down step by step:

• Start with the original function: \( y = x^2 - 2x + 1 \).
• To translate this function horizontally, replace \( x \) with \( x - h \). Here, \( h = 3 \), so we replace \( x \) with \( x - 3 \).
• Substitute \( x - 3 \) into the original function: \( y = (x - 3)^2 - 2(x - 3) + 1 \).
• This results in a horizontal translation of the graph to the right by 3 units.

The graphs of these two functions are shown above:

The blue graph represents \( y = x^2 - 2x + 1 \), and the red graph represents \( y = (x - 3)^2 - 2(x - 3) + 1 \). The red graph is shifted 3 units to the right compared to the blue graph.

Worked Examples on Graph Translations

Worked Example 2.11

The graph of \( y = x^2 + 5x \) is translated 2 units to the right. Find the equation of the resulting graph. Give your answer in the form \( y = ax^2 + bx + c \).

Steps:

1. Original Function:

2. Translation by 2 Units to the Right:

To translate the graph 2 units to the right, replace \( x \) with \( x - 2 \) in the original function.

3. Expanding and Simplifying:

Expand \( (x - 2)^2 \):

Distribute the \( 5 \) in \( 5(x - 2) \):

Combine all the terms:

Simplify the expression:

4. Final Answer:

Worked Example 2.12

The graph of \( y = \sqrt{2x} \) is translated by the vector \( \begin{pmatrix} -5 \\ 3 \end{pmatrix} \). Find the equation of the resulting graph.

Steps:

1. Original Function:

2. Horizontal Translation by -5 Units:

The vector \( \begin{pmatrix} -5 \\ 3 \end{pmatrix} \) indicates a translation 5 units to the left and 3 units up.

To translate the graph 5 units to the left, replace \( x \) with \( x + 5 \) in the original function.

3. Vertical Translation by 3 Units Up:

To translate the graph 3 units up, add 3 to the resulting function:

4. Expanding and Simplifying:

Distribute the \( 2 \) in \( 2(x + 5) \):

Combine the terms:

5. Final Answer:

Graph Transformations: Step-by-Step Solutions

Problem 1a:

The graph of \( y = 2x^2 \) is translated by the vector \( \begin{pmatrix} 0 \\ 4 \end{pmatrix} \).

Steps:

1. Original Function:

2. Translation by \( \begin{pmatrix} 0 \\ 4 \end{pmatrix} \):

This vector indicates a vertical translation of 4 units up. To apply this translation, add 4 to the function:

Final Answer:

Problem 1b:

The graph of \( y = 5\sqrt{x} \) is translated by the vector \( \begin{pmatrix} 0 \\ -2 \end{pmatrix} \).

Steps:

1. Original Function:

2. Translation by \( \begin{pmatrix} 0 \\ -2 \end{pmatrix} \):

This vector indicates a vertical translation of 2 units down. To apply this translation, subtract 2 from the function:

Final Answer:

Problem 1c:

The graph of \( y = 7x^2 - 2x \) is translated by the vector \( \begin{pmatrix} 0 \\ 1 \end{pmatrix} \).

Steps:

1. Original Function:

2. Translation by \( \begin{pmatrix} 0 \\ 1 \end{pmatrix} \):

This vector indicates a vertical translation of 1 unit up. To apply this translation, add 1 to the function:

Final Answer:

Problem 1d:

The graph of \( y = x^2 - 1 \) is translated by the vector \( \begin{pmatrix} 0 \\ 2 \end{pmatrix} \).

Steps:

1. Original Function:

2. Translation by \( \begin{pmatrix} 0 \\ 2 \end{pmatrix} \):

This vector indicates a vertical translation of 2 units up. To apply this translation, add 2 to the function:

Simplifying:

Final Answer:

Problem 1e:

The graph of \( y = \frac{2}{x} \) is translated by the vector \( \begin{pmatrix} -5 \\ 0 \end{pmatrix} \).

Steps:

1. Original Function:

2. Translation by \( \begin{pmatrix} -5 \\ 0 \end{pmatrix} \):

This vector indicates a horizontal translation of 5 units to the left. To apply this translation, replace \( x \) with \( x + 5 \) in the function:

Final Answer:

Problem 1f:

The graph of \( y = \frac{x}{x + 1} \) is translated by the vector \( \begin{pmatrix} 3 \\ 0 \end{pmatrix} \).

Steps:

1. Original Function:

2. Translation by \( \begin{pmatrix} 3 \\ 0 \end{pmatrix} \):

This vector indicates a horizontal translation of 3 units to the right. To apply this translation, replace \( x \) with \( x - 3 \) in the function:

Final Answer:

Problem 1g:

The graph of \( y = x^2 + x \) is translated by the vector \( \begin{pmatrix} -1 \\ 0 \end{pmatrix} \).

Steps:

1. Original Function:

2. Translation by \( \begin{pmatrix} -1 \\ 0 \end{pmatrix} \):

This vector indicates a horizontal translation of 1 unit to the left. To apply this translation, replace \( x \) with \( x + 1 \) in the function:

3. Expanding and Simplifying:

Expand \( (x + 1)^2 \):

Now combine all the terms:

Final Answer:

Problem 1h:

The graph of \( y = 3x^2 - 2 \) is translated by the vector \( \begin{pmatrix} 2 \\ 3 \end{pmatrix} \).

Steps:

1. Original Function:

2. Horizontal Translation by 2 Units Right:

Replace \( x \) with \( x - 2 \):

3. Vertical Translation by 3 Units Up:

Add 3 to the function:

Final Answer:

Find the Translation that Transforms the Graph

Graph Translations: Step-by-Step Solutions

Problem 2a:

Transform the graph \( y = x^2 + 5x - 2 \) to the graph \( y = x^2 + 5x + 2 \).

Steps:

1. Original Function:

2. Identifying the Translation:

The difference between the two functions is the constant term. The original function has \(-2\) and the transformed function has \(+2\). This suggests a vertical translation.

To transform \( y = x^2 + 5x - 2 \) into \( y = x^2 + 5x + 2 \), add 4 to the function.

Problem 2b:

Transform the graph \( y = x^3 + 2x^2 + 1 \) to the graph \( y = x^3 + 2x^2 - 4 \).

Steps:

1. Original Function:

2. Identifying the Translation:

The difference between the two functions is the constant term. The original function has \(+1\) and the transformed function has \(-4\). This suggests a vertical translation.

To transform \( y = x^3 + 2x^2 + 1 \) into \( y = x^3 + 2x^2 - 4 \), subtract 5 from the function.

Problem 2c:

Transform the graph \( y = x^2 - 3x \) to the graph \( y = (x + 1)^2 - 3(x + 1) \).

Steps:

1. Original Function:

2. Identifying the Translation:

The transformation involves replacing \( x \) with \( x + 1 \), which indicates a horizontal translation.

To transform \( y = x^2 - 3x \) into \( y = (x + 1)^2 - 3(x + 1) \), replace \( x \) with \( x + 1 \).

Problem 2d:

Transform the graph \( y = x + \frac{6}{x} \) to the graph \( y = x - 2 + \frac{6}{x - 2} \).

Steps:

1. Original Function:

2. Identifying the Translation:

The transformation involves replacing \( x \) with \( x - 2 \), which indicates a horizontal translation.

To transform \( y = x + \frac{6}{x} \) into \( y = x - 2 + \frac{6}{x - 2} \), replace \( x \) with \( x - 2 \).

Problem 2e:

Transform the graph \( y = \sqrt{2x} + 5 \) to the graph \( y = \sqrt{2x} + 3 \).

Steps:

1. Original Function:

2. Identifying the Translation:

The difference between the two functions is the constant term. The original function has \(+5\) and the transformed function has \(+3\). This suggests a vertical translation.

To transform \( y = \sqrt{2x} + 5 \) into \( y = \sqrt{2x} + 3 \), subtract 2 from the function.

Problem 2f:

Transform the graph \( y = \frac{5}{x^2} - 3x \) to the graph \( y = \frac{5}{(x - 2)^2} - 3x + 10 \).

Steps:

1. Original Function:

2. Identifying the Translation:

The transformation involves replacing \( x \) with \( x - 2 \) and adding 10 to the constant term. This indicates a horizontal translation and a vertical translation.

To transform \( y = \frac{5}{x^2} - 3x \) into \( y = \frac{5}{(x - 2)^2} - 3x + 10 \), replace \( x \) with \( x - 2 \) and then add 10.

Worked problems Chapter 2-functions Pg55- continued...

Graph Translations: Step-by-Step Solutions

Problem 5:

A cubic graph has the equation \( y = (x + 3)(x - 2)(x - 5) \). Write, in a similar form, the equation of the graph after a translation of \( \begin{pmatrix} 2 \\ 0 \end{pmatrix} \).

Steps:

1. Original Function:

2. Translation by \( \begin{pmatrix} 2 \\ 0 \end{pmatrix} \):

This vector indicates a horizontal translation of 2 units to the right. To apply this translation, replace \( x \) with \( x - 2 \) in the function.

3. Simplify the Expression:

Now, simplify each factor:

Final Answer:

Problem 6:

The graph of \( y = x^2 - 4x + 1 \) is translated by the vector \( \begin{pmatrix} 1 \\ 2 \end{pmatrix} \). Find, in the form \( y = ax^2 + bx + c \), the equation of the resulting graph.

Steps:

1. Original Function:

2. Horizontal Translation by 1 Unit Right:

Replace \( x \) with \( x - 1 \) in the function:

3. Expanding and Simplifying:

Expand \( (x - 1)^2 \):

Distribute \( -4 \) in \( -4(x - 1) \):

Now combine all the terms:

4. Vertical Translation by 2 Units Up:

Now add 2 to the function:

Simplify:

Final Answer:

Problem 7:

The graph of \( y = ax^2 + bx + c \) is translated by the vector \( \begin{pmatrix} 2 \\ -5 \end{pmatrix} \). The resulting graph is \( y = 2x^2 - 11x + 10 \). Find the value of \( a \), the value of \( b \), and the value of \( c \).

Steps:

1. Original Function:

2. Translation by \( \begin{pmatrix} 2 \\ -5 \end{pmatrix} \):

To apply the horizontal translation, replace \( x \) with \( x - 2 \) in the original function:

3. Expand and Simplify:

Expand \( (x - 2)^2 \):

Distribute \( b \) in \( b(x - 2) \):

Substitute and simplify:

4. Apply Vertical Translation by -5 Units Down:

Subtract 5 from the function:

5. Comparing with the Resulting Function:

Given the resulting function \( y = 2x^2 - 11x + 10 \), we equate coefficients:

Substituting \( a = 2 \) into the equations:

Final Values:

Reflections in Graphs: Detailed Notes

Understanding Reflections

Reflection: A transformation that "flips" a graph over a specified line, such as the x-axis or y-axis, producing a mirror image of the original graph. The most common types of reflections are:

• Reflection over the x-axis: This type of reflection is achieved by multiplying the entire function by \(-1\). If the original function is \( y = f(x) \), then the reflected function is \( y = -f(x) \).


• Reflection over the y-axis: This type of reflection is achieved by replacing \( x \) with \(-x\) in the function. If the original function is \( y = f(x) \), then the reflected function is \( y = f(-x) \).

Example: Reflection Over the x-axis

Consider the function \( y = x^2 - 2x + 1 \). The reflection of this function over the x-axis can be found by multiplying the entire function by \(-1\).

The original function is:

The reflected function is:

When these two functions are graphed, they are mirror images of each other across the x-axis. This means that for every point \((x, y)\) on the original graph, there is a corresponding point \((x, -y)\) on the reflected graph.

Key Observations:

• For every \( x \) value, the y-coordinates of the reflected graph are the negative of the y-coordinates of the original graph.


• The shapes of the original graph and the reflected graph are identical, but they are positioned on opposite sides of the x-axis.

Example: Reflection Over the y-axis

Consider the function \( y = (x - 3)^2 + 2 \). The reflection of this function over the y-axis can be found by replacing \( x \) with \(-x\) in the function.

The original function is:

The reflected function is:

This operation reflects the graph over the y-axis. The result is that for every point \((x, y)\) on the original graph, there is a corresponding point \((-x, y)\) on the reflected graph.

Key Observations:

• The y-coordinates remain unchanged, but the x-coordinates are the negative of those in the original graph.


• The shapes of the original graph and the reflected graph are identical, but they are positioned on opposite sides of the y-axis.

Conclusion:

Reflections are a fundamental type of transformation that can be used to understand how graphs behave under certain operations. By reflecting a graph over the x-axis or y-axis, we can visualize how the graph would look if flipped across these axes. This concept is widely used in various mathematical applications and helps in understanding symmetry in functions.

Solved Examples

Reflections: Step-by-Step Solutions

Problem 2a:

Find the equation of the graph \( y = 5x^2 \) after reflection in the x-axis.

Steps:

1. Original Function:

2. Reflection in the x-axis:

To reflect the graph over the x-axis, multiply the entire function by \(-1\):

Final Answer:

Problem 2b:

Find the equation of the graph \( y = 2x^4 \) after reflection in the y-axis.

Steps:

1. Original Function:

2. Reflection in the y-axis:

To reflect the graph over the y-axis, replace \( x \) with \(-x\) in the function:

3. Simplify:

Since \((-x)^4 = x^4\), the equation remains the same:

Final Answer:

(Note: The reflection over the y-axis does not change the graph because \( x^4 \) is an even function.)

Problem 2c:

Find the equation of the graph \( y = 2x^2 - 3x + 1 \) after reflection in the y-axis.

Steps:

1. Original Function:

2. Reflection in the y-axis:

To reflect the graph over the y-axis, replace \( x \) with \(-x\) in the function:

3. Simplify:

Simplify each term:

Final Answer:

Problem 2d:

Find the equation of the graph \( y = 5 + 2x - 3x^2 \) after reflection in the x-axis.

Steps:

1. Original Function:

2. Reflection in the x-axis:

To reflect the graph over the x-axis, multiply the entire function by \(-1\):

3. Distribute \(-1\):

Distribute the negative sign across the function:

Final Answer:

Transformation Descriptions: Step-by-Step Solutions

Problem 3a:

Describe the transformation that maps the graph \( y = x^2 + 7x - 3 \) onto the graph \( y = -x^2 - 7x + 3 \).

Steps:

1. Compare the Original and Transformed Functions:

2. Identify the Transformation:

Notice that the entire function has been multiplied by \(-1\), which indicates a reflection over the x-axis.

Final Answer:

The transformation that maps the original graph onto the new graph is a reflection over the x-axis.

Problem 3b:

Describe the transformation that maps the graph \( y = x^2 - 3x + 4 \) onto the graph \( y = x^2 + 3x + 4 \).

Steps:

1. Compare the Original and Transformed Functions:

2. Identify the Transformation:

Notice that the sign of the linear term \( -3x \) has changed to \( +3x \), which indicates a reflection over the y-axis.

Final Answer:

The transformation that maps the original graph onto the new graph is a reflection over the y-axis.

Problem 3c:

Describe the transformation that maps the graph \( y = 2x - 5x^2 \) onto the graph \( y = 5x^2 - 2x \).

Steps:

1. Compare the Original and Transformed Functions:

2. Identify the Transformation:

Notice that the terms in the function have been reordered, with their signs reversed. This transformation involves both a reflection over the y-axis and a rearrangement of the terms.

Final Answer:

The transformation that maps the original graph onto the new graph is a reflection over the y-axis followed by rearranging the terms.

Problem 3d:

Describe the transformation that maps the graph \( y = x^3 + 2x^2 - 3x + 1 \) onto the graph \( y = -x^3 - 2x^2 + 3x - 1 \).

Steps:

1. Compare the Original and Transformed Functions:

2. Identify the Transformation:

Notice that the entire function has been multiplied by \(-1\), which indicates a reflection over the x-axis.

Final Answer:

The transformation that maps the original graph onto the new graph is a reflection over the x-axis.

Question: 1

Step-by-Step Solutions

Question

i. Express \( -x^2 + 6x - 5 \) in the form \( a(x + b)^2 + c \), where \( a \), \( b \), and \( c \) are constants.

ii. State the smallest possible value of \( m \) for which \( f \) is one-one.

iii. For the case where \( m = 5 \), find an expression for \( f^{-1}(x) \) and state the domain of \( f^{-1} \).

Solution:

i. Express \( -x^2 + 6x - 5 \) in the form \( a(x + b)^2 + c \)

We begin by completing the square for the quadratic expression:

Step 1: Factor out the negative sign from the first two terms:

Step 2: Complete the square inside the parentheses. To complete the square, take half of the coefficient of \( x \) (which is \( -6 \)), square it, and add it and subtract it inside the parentheses:

Step 3: Factor the perfect square trinomial:

Thus, the expression in the required form is:

Here, \( a = -1 \), \( b = -3 \), and \( c = 4 \).

ii. State the smallest possible value of \( m \) for which \( f \) is one-one.

For a quadratic function to be one-one, it must either be strictly increasing or strictly decreasing. From the completed square form \( f(x) = -(x - 3)^2 + 4 \), we know that the vertex of the parabola is at \( x = 3 \), and the function is decreasing for \( x \leq 3 \) and increasing for \( x \geq 3 \). To make \( f \) one-one, we restrict the domain to values of \( x \) greater than or equal to the vertex.

The smallest possible value of \( m \) for which \( f \) is one-one is:

iii. For the case where \( m = 5 \), find an expression for \( f^{-1}(x) \) and state the domain of \( f^{-1} \).

Given that \( m = 5 \), the function \( f(x) = -(x - 3)^2 + 4 \) is defined for \( x \geq 5 \).

We will find the inverse function \( f^{-1}(x) \). Start by setting \( y = -(x - 3)^2 + 4 \) and solving for \( x \):

Step 1: Subtract 4 from both sides:

Step 2: Multiply both sides by -1:

Step 3: Take the square root of both sides:

Step 4: Solve for \( x \):

The inverse function is:

The domain of the inverse function is restricted to values of \( x \) for which \( -(x - 4) \geq 0 \), or equivalently:

Final Answer:

i. \( -(x - 3)^2 + 4 \)

ii. \( m = 3 \)

iii. \( f^{-1}(x) = 3 + \sqrt{-(x - 4)} \), Domain: \( x \leq 4 \)

Question: 2

Step-by-Step Solutions

Question

The function \( f : x \mapsto x^2 - 4x + k \) is defined for the domain \( x \geq p \), where \( k \) and \( p \) are constants.

i. Express \( f(x) \) in the form \( (x + a)^2 + b + k \), where \( a \) and \( b \) are constants.

ii. State the range of \( f \) in terms of \( k \).

iii. State the smallest possible value of \( p \) for which \( f \) is one-one.

iv. For the value of \( p \) found in part iii, find an expression for \( f^{-1}(x) \) and state the domain of \( f^{-1} \), giving your answer in terms of \( k \).

Solution:

i. Express \( f(x) \) in the form \( (x + a)^2 + b + k \)

We begin by completing the square for the quadratic expression:

Step 1: Factor out any constants from the first two terms:

Step 2: Complete the square inside the parentheses. To complete the square, take half of the coefficient of \( x \) (which is \( -4 \)), square it, and add it and subtract it inside the parentheses:

Thus, the expression in the required form is:

Here, \( a = -2 \), and \( b = -4 \).

ii. State the range of \( f \) in terms of \( k \)

From the expression \( f(x) = (x - 2)^2 + k - 4 \), we know that the minimum value of \( (x - 2)^2 \) is 0, as squares are always non-negative. Therefore, the minimum value of \( f(x) \) occurs when \( (x - 2)^2 = 0 \), which gives:

Thus, the range of \( f(x) \) is:

iii. State the smallest possible value of \( p \) for which \( f \) is one-one.

For a quadratic function to be one-one, we need to restrict the domain such that the function is either strictly increasing or strictly decreasing. From the expression \( f(x) = (x - 2)^2 + k - 4 \), we know that the vertex of the parabola occurs at \( x = 2 \), and the function is increasing for \( x \geq 2 \).

Therefore, the smallest possible value of \( p \) for which \( f \) is one-one is:

iv. For the value of \( p = 2 \), find an expression for \( f^{-1}(x) \) and state the domain of \( f^{-1} \), giving your answer in terms of \( k \).

We are given that \( p = 2 \), so the function \( f(x) = (x - 2)^2 + k - 4 \) is defined for \( x \geq 2 \).

We will find the inverse function \( f^{-1}(x) \). Start by setting \( y = (x - 2)^2 + k - 4 \) and solving for \( x \):

Step 1: Subtract \( k - 4 \) from both sides:

Step 2: Take the square root of both sides (since the domain of \( f \) is restricted to \( x \geq 2 \), we only take the positive square root):

Step 3: Solve for \( x \):

The inverse function is:

The domain of \( f^{-1}(x) \) is the range of \( f(x) \), which we found to be \( f(x) \geq k - 4 \). Therefore, the domain of \( f^{-1}(x) \) is:

Final Answer:

i. \( f(x) = (x - 2)^2 + k - 4 \)

ii. \( f(x) \geq k - 4 \)

iii. \( p = 2 \)

iv. \( f^{-1}(x) = 2 + \sqrt{x - (k - 4)} \), Domain: \( x \geq k - 4 \)

Question: 3

Step-by-Step Solutions

Question:

The function \( f \) is defined as:

i. State the range of \( f \).

ii. Copy the diagram and sketch the graph of \( y = f^{-1}(x) \).

iii. Obtain expressions to define the function \( f^{-1}(x) \), giving the set of values for which each expression is valid.

Solution:

i. State the range of \( f \)

First, we evaluate the range of each piece of the function:

Thus, the range of the entire function \( f(x) \) is:

ii. Copy the diagram and sketch the graph of \( y = f^{-1}(x) \)

The graph of the inverse function \( y = f^{-1}(x) \) is obtained by reflecting the graph of \( f(x) \) over the line \( y = x \). To sketch the graph:

The graph of \( f^{-1}(x) \) can now be sketched accordingly by reflecting these points and ensuring the correct piecewise behavior of the inverse function.

iii. Obtain expressions to define the function \( f^{-1}(x) \), giving the set of values for which each expression is valid

We now need to find the inverse of each piece of \( f(x) \) and specify the domain for each:

Final Answer:

i. Range of \( f(x) \): \( [-5, 4] \)

ii. See graph of \( y = f^{-1}(x) \), which is the reflection of \( f(x) \) over the line \( y = x \).

iii. The inverse function is:

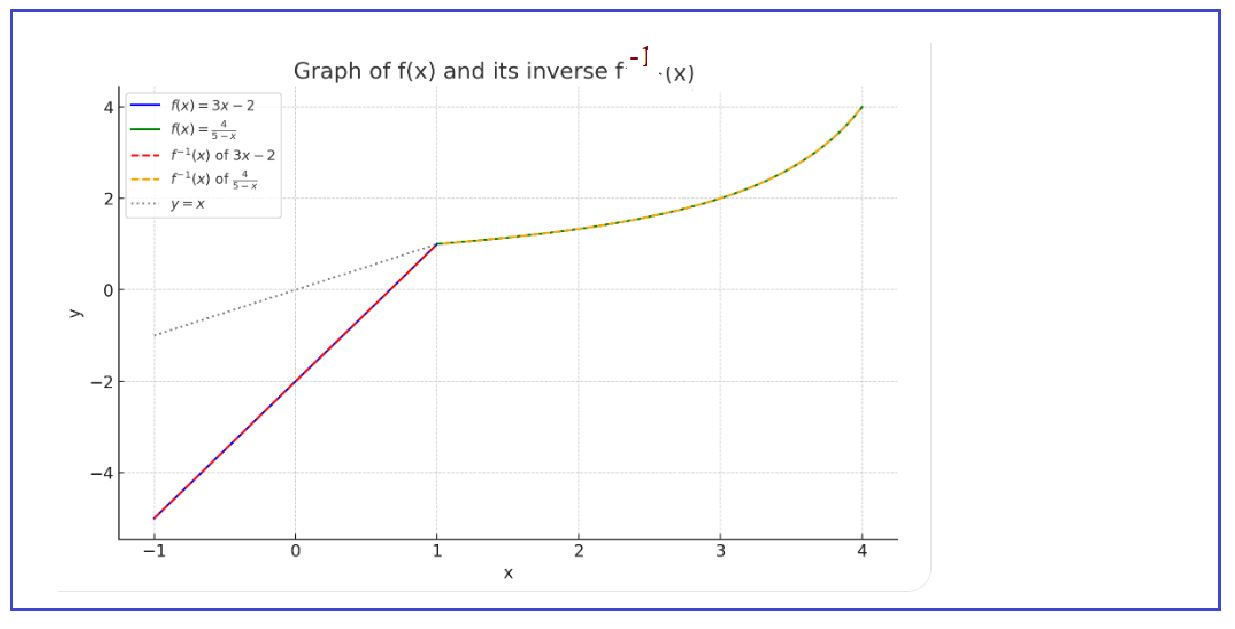
Step-by-Step Solutions

Question:

The function \( f(x) = 2x^2 - 12x + 13 \) is defined as follows:

i. Express \( 2x^2 - 12x + 13 \) in the form \( a(x + b)^2 + c \), where \( a \), \( b \), and \( c \) are constants.

Solution:

We will complete the square to express the quadratic in the required form:

Now, complete the square for \( x^2 - 6x \):

Thus:

Simplifying:

Thus, the expression in the required form is:

ii. The function \( f(x) = 2x^2 - 12x + 13 \) is defined for \( x \geq k \), where \( k \) is a constant. It is given that \( f \) is a one-to-one function. State the smallest possible value of \( k \).

In order for the quadratic function to be one-to-one, we need to restrict the domain so that the function is either strictly increasing or strictly decreasing. The function \( f(x) = 2(x - 3)^2 - 5 \) has a minimum value when \( x = 3 \), which is the vertex of the parabola.

To make \( f \) one-to-one, we restrict the domain to \( x \geq 3 \), so that the function is strictly increasing. Thus, the smallest possible value of \( k \) is:

iii. Find the range of \( f \).

The range of \( f(x) = 2(x - 3)^2 - 5 \) is determined by the fact that the minimum value of \( (x - 3)^2 \) is 0, since squares are always non-negative.

Thus, the minimum value of \( f(x) \) is:

Since the function is strictly increasing for \( x \geq 3 \), the range of \( f(x) \) is:

iv. Find the expression for \( f^{-1}(x) \) and state the domain of \( f^{-1} \).

We start by setting \( y = 2(x - 3)^2 - 5 \) and solve for \( x \):

Now, take the square root of both sides:

Since \( f(x) \) is defined for \( x \geq 3 \), the domain of \( f^{-1}(x) \) is the range of \( f(x) \), which is \( x \geq -5 \). Thus, the domain of \( f^{-1}(x) \) is:

Question

i. Express \( x^2 - 2x - 15 \) in the form \( (x + a)^2 + b \).

Solution:

We will complete the square for the expression \( x^2 - 2x - 15 \).

Step 1: Take the quadratic part \( x^2 - 2x \) and complete the square:

Step 2: Substitute this back into the original expression:

Thus, the expression in the required form is:

ii. State the smallest possible value of \( c \).

Since \( f(x) = (x - 1)^2 - 16 \), the minimum value of \( (x - 1)^2 \) is 0 (because squares are non-negative). Therefore, the smallest value of \( f(x) \) is:

Thus, the smallest possible value of \( c \) is:

iii. For the case where \( c = 9 \) and \( d = 65 \), find \( p \) and \( q \).

We are given that \( f(x) \) is bounded between 9 and 65. From the equation \( f(x) = (x - 1)^2 - 16 \), set \( f(x) = 9 \) and solve for \( x \):

So, \( p = -4 \) and \( q = 6 \).

iv. Find an expression for \( f^{-1}(x) \) and state the domain of \( f^{-1} \).

To find the inverse function \( f^{-1}(x) \), we start by setting \( y = (x - 1)^2 - 16 \) and solve for \( x \):

Take the square root of both sides:

So:

Since \( f(x) \) is defined for \( x \geq -4 \), we take the positive square root:

The domain of \( f^{-1}(x) \) is the range of \( f(x) \), which is \( 9 \leq x \leq 65 \). Therefore, the domain of \( f^{-1}(x) \) is:

Question

Step-by-Step Solution

i. Express \( f(x) \) in the form \( a(x - b)^2 - c \)

We are given the function:

To express \( f(x) \) in the form \( a(x - b)^2 - c \), we need to complete the square.

Step 1: Factor out 2 from the quadratic terms:

Step 2: Complete the square for the expression inside the parentheses:

Substitute this back into the equation:

Step 3: Simplify the expression:

Thus, the expression in the required form is:

ii. State the range of \( f \)

The function \( f(x) = 2(x - 3)^2 - 11 \) is a parabola that opens upwards (since the coefficient of \( (x - 3)^2 \) is positive).

The minimum value of \( f(x) \) occurs when \( (x - 3)^2 = 0 \), which gives:

Therefore, the range of \( f(x) \) is:

iii. Find the set of values of \( x \) for which \( f(x) < 21 \)

We are given that \( f(x) = 2(x - 3)^2 - 11 \), and we need to find the values of \( x \) for which \( f(x) < 21 \).

Step 1: Set the inequality:

Step 2: Add 11 to both sides:

Step 3: Divide both sides by 2:

Step 4: Take the square root of both sides:

Step 5: Solve for \( x \):

Therefore, the set of values of \( x \) for which \( f(x) < 21 \) is:

iv. Find the value of the constant \( k \) for which the equation \( g(f(x)) = 0 \) has two equal roots

We are given that \( g(x) = 2x + k \) and need to find \( k \) such that \( g(f(x)) = 0 \) has two equal roots.

First, express \( g(f(x)) = 0 \):

Substitute \( f(x) = 2(x - 3)^2 - 11 \) into the equation:

Simplify:

For the equation to have two equal roots, the expression inside the parentheses \( (x - 3)^2 \) must be zero, which occurs when \( x = 3 \).

Substitute \( x = 3 \) into the equation:

Thus, \( k = 22 \).

Worked Examples

Q1

What was the primary reason for the collapse of the Bronze Age civilizations around 1200 BCE?

Solution:

• The collapse is attributed to a combination of factors, including natural disasters, invasions by the Sea Peoples, internal social upheavals, and a breakdown in trade networks.
• This disrupted the supply of tin and copper necessary for making bronze, leading to the downfall of major civilizations such as the Mycenaeans, Hittites, and Egyptians.

Q2

What is the "Ship of Theseus" paradox, and what does it question about identity?

Solution:

• The "Ship of Theseus" paradox asks whether a ship that has had all its components replaced remains fundamentally the same ship.
• This paradox challenges the concept of identity, questioning whether an object that undergoes gradual change can still be considered the same object.

Q3

What is Gödel's Incompleteness Theorem, and how does it impact mathematical systems?

Solution:

• Gödel's Incompleteness Theorem states that in any consistent mathematical system, there are statements that are true but cannot be proven within that system.
• This means that no mathematical system can be both complete and consistent, implying that some truths will always lie beyond formal proof.

Q4

What is the "Fermi Paradox," and what does it question about extraterrestrial life?

Solution:

• The Fermi Paradox questions why, despite the high probability of extraterrestrial life, we have not yet encountered any evidence of other civilizations.
• This paradox highlights the apparent contradiction between the vastness of the universe and the lack of observational evidence of alien life.

Q5

What is the Sapir-Whorf Hypothesis, and how does it influence our understanding of language and thought?

Solution:

• The Sapir-Whorf Hypothesis posits that the structure of a language influences its speakers' cognition and worldview.
• It suggests that people who speak different languages perceive and think about the world differently because language shapes thought processes.

Q6

What is the "Red Queen Hypothesis," and how does it relate to evolutionary biology?

Solution:

• The Red Queen Hypothesis suggests that organisms must constantly adapt and evolve to survive in an ever-changing environment where other species are also evolving.
• This concept emphasizes continuous evolutionary arms races between species.

Q7

What is the significance of Göbekli Tepe, and how does it challenge traditional views of human civilization?

Solution:

• Göbekli Tepe is significant because it predates the advent of agriculture and permanent settlements.
• This challenges the traditional view that complex societies developed only after the establishment of agriculture and suggests that organized religion and monumental architecture may have preceded farming.

Q8

What is the "Dunning-Kruger Effect," and how does it influence people's perception of their abilities?

Solution:

• The Dunning-Kruger Effect is a cognitive bias in which people with low ability or knowledge overestimate their competence, while those with high competence tend to underestimate their abilities.
• This effect highlights the lack of self-awareness in individuals regarding their own skills.

Q9

What is the "Paradox of Thrift," and how does it relate to macroeconomic theory?

Solution:

• The Paradox of Thrift suggests that while saving money is beneficial for individuals, if everyone saves more during a recession, overall demand will fall, leading to lower total savings and a weaker economy.
• This paradox illustrates the conflict between individual rationality and collective outcomes in economics.

Q10

What is the significance of the "Arnolfini Portrait" by Jan van Eyck, and what are its key symbolic elements?

Solution:

• The "Arnolfini Portrait" is significant for its intricate detail and use of symbolism.
• Key elements include the mirror reflecting the scene, the dog symbolizing loyalty, and the use of light to create depth and realism, often interpreted as a visual contract or depiction of marriage.

Vocabulary for Graph Transformations

Key Terms and Definitions

Function: A relationship between inputs and outputs where each input is related to exactly one output.

Graph: A visual representation of a function on a coordinate plane.

Translation: A transformation that moves every point on a graph a certain distance in a specified direction. Translations can be vertical (up/down) or horizontal (left/right).

Horizontal Translation: The shifting of a graph left or right on the coordinate plane. Achieved by replacing \( x \) with \( x - h \) (right) or \( x + h \) (left) in the function.

Vertical Translation: The shifting of a graph up or down on the coordinate plane. Achieved by adding or subtracting a constant \( c \) to/from the function.

Reflection: A transformation that flips the graph over a specified line, such as the x-axis or y-axis. For example, \( y = -f(x) \) reflects the graph over the x-axis.

Stretching: A transformation that pulls the graph away from the x-axis or y-axis, making it appear "stretched." Vertical stretching is achieved by multiplying the function by a constant greater than 1.

Compression: A transformation that pushes the graph toward the x-axis or y-axis, making it appear "compressed." Vertical compression is achieved by multiplying the function by a constant between 0 and 1.

Horizontal Stretch: Achieved by replacing \( x \) with \( \frac{x}{k} \) in the function, where \( k > 1 \) stretches the graph horizontally.

Vertical Stretch: Achieved by multiplying the function by a constant \( a \), where \( a > 1 \) stretches the graph vertically.

Horizontal Compression: Achieved by replacing \( x \) with \( \frac{x}{k} \) in the function, where \( 0 < k < 1 \) compresses the graph horizontally.

Vertical Compression: Achieved by multiplying the function by a constant \( a \), where \( 0 < a < 1 \) compresses the graph vertically.

Vertex: The highest or lowest point on the graph of a parabola (in the case of quadratic functions). For example, the vertex of \( y = ax^2 + bx + c \) is at \( x = -\frac{b}{2a} \).

Axis of Symmetry: A line that divides the graph into two mirror-image halves. For parabolas, this line is vertical and passes through the vertex.

Quadratic Function: A function of the form \( y = ax^2 + bx + c \), where the graph is a parabola.

Linear Function: A function of the form \( y = mx + b \), where the graph is a straight line.

Absolute Value Function: A function that returns the absolute value of the input, typically written as \( y = |x| \). The graph is V-shaped.

Radical Function: A function that involves a square root, cube root, or other roots, such as \( y = \sqrt{x} \). The graph generally has a curve that starts at a certain point.

Rational Function: A function that is the ratio of two polynomials, such as \( y = \frac{1}{x} \). The graph often has asymptotes and a hyperbolic shape.

Asymptote: A line that the graph of a function approaches but never touches. Asymptotes can be vertical, horizontal, or oblique.

Translation: A transformation that shifts a graph horizontally, vertically, or both, without altering its shape or orientation.

Horizontal Translation: A transformation that shifts a graph left or right on the coordinate plane.

Vertical Translation: A transformation that shifts a graph up or down on the coordinate plane.

Reflection: A transformation that "flips" a graph over a specified line, such as the x-axis or y-axis.

Transformation: A general term referring to any change applied to a graph, including translations, reflections, stretches, and compressions.

Vector: A quantity having both magnitude and direction, often used to describe the direction and distance of a translation.

Horizontal Shift: Another term for a horizontal translation.

Vertical Shift: Another term for a vertical translation.

Function Notation: A way of representing functions that is useful in describing transformations. For example, \( y = f(x) \) can be transformed into \( y = f(x - h) + k \) to describe a translation.

Algebra Week 2 Teaching Plan

Q1 (Find the Vertex and Axis of Symmetry for \( f(x) = x^2 + 8x - 1 \))

Given: \( f(x) = x^2 + 8x - 1 \)

Solution:

• Complete the square: \[ f(x) = x^2 + 8x + \left(\frac{8}{2}\right)^2 - \left(\frac{8}{2}\right)^2 - 1 = (x + 4)^2 - 17 \]
• The vertex is \( (-4, -17) \).
• The formula for the axis of symmetry is \( x = -\frac{b}{2a} \). For this equation, \( a = 1 \) and \( b = 8 \), so: \[ x = -\frac{8}{2(1)} = -4 \]
• The axis of symmetry is \( x = -4 \).

Q2 (Find the Vertex and Axis of Symmetry for \( f(x) = x^2 + 10x + 25 \))

Given: \( f(x) = x^2 + 10x + 25 \)

Solution:

• Recognize that this is a perfect square: \[ f(x) = (x + 5)^2 \]
• The vertex is \( (-5, 0) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = 1 \) and \( b = 10 \): \[ x = -\frac{10}{2(1)} = -5 \]
• The axis of symmetry is \( x = -5 \).

Q3 (Find the Vertex and Axis of Symmetry for \( f(x) = -x^2 + 2x + 5 \))

Given: \( f(x) = -x^2 + 2x + 5 \)

Solution:

• Factor out the negative sign and complete the square: \[ f(x) = -\left(x^2 - 2x + 1 - 1 + 5\right) = -(x - 1)^2 + 6 \]
• The vertex is \( (1, 6) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -1 \) and \( b = 2 \): \[ x = -\frac{2}{2(-1)} = 1 \]
• The axis of symmetry is \( x = 1 \).

Q4 (Find the Vertex and Axis of Symmetry for \( f(x) = -2x^2 - 8x - 3 \))

Given: \( f(x) = -2x^2 - 8x - 3 \)

Solution:

• Factor out the -2 and complete the square: \[ f(x) = -2\left(x^2 + 4x + 4 - 4 - \frac{3}{2}\right) = -2(x + 2)^2 + 5 \]
• The vertex is \( (-2, 5) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -2 \) and \( b = -8 \): \[ x = -\frac{-8}{2(-2)} = -2 \]
• The axis of symmetry is \( x = -2 \).

Q5 (Find the Vertex and Axis of Symmetry for \( y = -x^2 + 10x - 34 \))

Given: \( y = -x^2 + 10x - 34 \)

Solution:

• Complete the square: \[ y = -(x^2 - 10x + 25 - 25 - 34) = -(x - 5)^2 - 9 \]
• The vertex is \( (5, -9) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -1 \) and \( b = 10 \): \[ x = -\frac{10}{2(-1)} = 5 \]
• The axis of symmetry is \( x = 5 \).

Q6 (Find the Vertex and Axis of Symmetry for \( y = -x^2 - 6x + 1 \))

Given: \( y = -x^2 - 6x + 1 \)

Solution:

• Complete the square: \[ y = -(x^2 + 6x + 9 - 9 + 1) = -(x + 3)^2 + 10 \]
• The vertex is \( (-3, 10) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -1 \) and \( b = -6 \): \[ x = -\frac{-6}{2(-1)} = -3 \]
• The axis of symmetry is \( x = -3 \).

Q7 (Find the Vertex and Axis of Symmetry for \( y = -4x^2 + 12x - 7 \))

Given: \( y = -4x^2 + 12x - 7 \)

Solution:

• Factor out the -4 and complete the square: \[ y = -4(x^2 - 3x + \frac{9}{4} - \frac{9}{4} - 7) = -4(x - \frac{3}{2})^2 + 2 \]
• The vertex is \( \left(\frac{3}{2}, 2\right) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -4 \) and \( b = 12 \): \[ x = -\frac{12}{2(-4)} = \frac{3}{2} \]
• The axis of symmetry is \( x = \frac{3}{2} \).

Q8: Find the Vertex and Axis of Symmetry for \( y = -9x^2 + 6x + 2 \)

Given: \( y = -9x^2 + 6x + 2 \)

Solution:

• Factor out the -9 and complete the square: \[ y = -9(x^2 - \frac{2}{3}x + \frac{1}{9} - \frac{1}{9} + 2) = -9(x - \frac{1}{3})^2 + 3 \]
• The vertex is \( \left(\frac{1}{3}, 3\right) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -9 \) and \( b = 6 \): \[ x = -\frac{6}{2(-9)} = \frac{1}{3} \]
• The axis of symmetry is \( x = \frac{1}{3} \).

Q9: Find the Vertex and Axis of Symmetry for \( y = 4x^2 - 1 \)

Given: \( y = 4x^2 - 1 \)

Solution:

• This is already a perfect square form: \[ y = 4(x)^2 - 1 \]
• The vertex is \( (0, -1) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = 4 \) and \( b = 0 \): \[ x = 0 \]
• The axis of symmetry is \( x = 0 \).

Q10: Find the Vertex and Axis of Symmetry for \( y = x^2 - 16 \)

Given: \( y = x^2 - 16 \)

Solution:

• This is already a perfect square form: \[ y = (x)^2 - 16 \]
• The vertex is \( (0, -16) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = 1 \) and \( b = 0 \): \[ x = 0 \]
• The axis of symmetry is \( x = 0 \).

Worked Examples

Q1 (Write \( y = 4x^2 + 8x - 5 \) in the form \( y = a(x + b)^2 + c \), where \( a \), \( b \), and \( c \) are integers)

Given: \( y = 4x^2 + 8x - 5 \)

Solution:

• First, factor out the coefficient of \( x^2 \) from the first two terms: \[ y = 4(x^2 + 2x) - 5 \]
• Now complete the square by adding and subtracting the square of half the coefficient of \( x \). Half of 2 is 1, and \( 1^2 = 1 \): \[ y = 4\left(x^2 + 2x + 1 - 1\right) - 5 \]
• Simplify the expression: \[ y = 4\left((x + 1)^2 - 1\right) - 5 \]
• Distribute the 4: \[ y = 4(x + 1)^2 - 4 - 5 \]
• Combine the constants: \[ y = 4(x + 1)^2 - 9 \]
• Thus, the quadratic function in the form \( y = a(x + b)^2 + c \) is: \[ y = 4(x + 1)^2 - 9 \] where \( a = 4 \), \( b = 1 \), and \( c = -9 \).

Intersection of a Quadratic Curve and a Line

Q2 (Find any points of intersection between the curve \( C \) and the line \( l \))

Given:

• Curve \( C \) has the equation \( y = x^2 - 3x + 2 \).
• Line \( l \) has the equation \( y = 3x - 7 \).

Solution:

• To find the points of intersection, set the equations for the curve and the line equal to each other: \[ x^2 - 3x + 2 = 3x - 7 \]
• Rearrange the equation to form a standard quadratic equation: \[ x^2 - 3x - 3x + 2 + 7 = 0 \implies x^2 - 6x + 9 = 0 \]
• Factor the quadratic equation: \[ (x - 3)^2 = 0 \]
• Solving for \( x \), we get: \[ x = 3 \]
• Substitute \( x = 3 \) back into the equation of the line to find the corresponding value of \( y \): \[ y = 3(3) - 7 = 9 - 7 = 2 \]
• Therefore, the point of intersection is \( (3, 2) \).

Worked Examples

Q1: Show that \( p^2 < 12q \) for the equation \( y = 3x^2 + 2px + 4q \) having no real roots

Given: \( y = 3x^2 + 2px + 4q \)

Solution:

• The general condition for a quadratic equation to have no real roots is that the discriminant must be less than zero. The discriminant \( \Delta \) of a quadratic equation \( ax^2 + bx + c = 0 \) is given by: \[ \Delta = b^2 - 4ac \]
• For the given equation \( y = 3x^2 + 2px + 4q \), the coefficients are: \[ a = 3, \quad b = 2p, \quad c = 4q \]
• Substituting these values into the discriminant formula: \[ \Delta = (2p)^2 - 4(3)(4q) = 4p^2 - 48q \]
• For the equation to have no real roots, the discriminant must be less than zero: \[ 4p^2 - 48q < 0 \]
• Simplifying the inequality: \[ 4p^2 < 48q \] Dividing both sides by 4: \[ p^2 < 12q \]
• Thus, we have shown that \( p^2 < 12q \).

Q2: Find the minimum value of the function \( f(x) = x^2 + 4x + c \), giving your answer in terms of \( c \)

Given: \( f(x) = x^2 + 4x + c \)

Solution:

• To find the minimum value of the function, we complete the square.
• First, factor the quadratic and linear terms: \[ f(x) = (x^2 + 4x) + c \]
• Complete the square by adding and subtracting the square of half the coefficient of \( x \). Half of 4 is 2, and \( 2^2 = 4 \): \[ f(x) = (x^2 + 4x + 4 - 4) + c = (x + 2)^2 - 4 + c \]
• The minimum value of \( (x + 2)^2 \) occurs when \( (x + 2)^2 = 0 \). Therefore, the minimum value of the function is: \[ f(x) = -4 + c \]
• Thus, the minimum value of the function is \( c - 4 \), and it occurs when \( x = -2 \).

Q3: Sketch the graph of \( y = 12x^2 - 5x - 72 \), labelling any points where the graph crosses the coordinate axes and the turning point

Given: \( y = 12x^2 - 5x - 72 \)

Solution:

• To sketch the graph, we need to find:
  • The x-intercepts (roots of the quadratic)
  • The y-intercept (value of \( y \) when \( x = 0 \))
  • The turning point (vertex of the parabola)

Step 1: Find the x-intercepts

• To find the x-intercepts, set \( y = 0 \) and solve the quadratic equation: \[ 12x^2 - 5x - 72 = 0 \]
• We can use the quadratic formula: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] where \( a = 12 \), \( b = -5 \), and \( c = -72 \).
• Substituting the values: \[ x = \frac{-(-5) \pm \sqrt{(-5)^2 - 4(12)(-72)}}{2(12)} = \frac{5 \pm \sqrt{25 + 3456}}{24} = \frac{5 \pm \sqrt{3481}}{24} = \frac{5 \pm 59}{24} \]
• This gives two solutions: \[ x = \frac{5 + 59}{24} = \frac{64}{24} = \frac{8}{3}, \quad x = \frac{5 - 59}{24} = \frac{-54}{24} = -\frac{9}{4} \]
• Therefore, the x-intercepts are \( x = \frac{8}{3} \) and \( x = -\frac{9}{4} \).

Step 2: Find the y-intercept

• To find the y-intercept, set \( x = 0 \): \[ y = 12(0)^2 - 5(0) - 72 = -72 \]
• The y-intercept is \( y = -72 \).

Step 3: Find the turning point

• We can find the turning point using the formula for the vertex \( x = -\frac{b}{2a} \). For the given equation, \( a = 12 \) and \( b = -5 \): \[ x = -\frac{-5}{2(12)} = \frac{5}{24} \]
• Substitute \( x = \frac{5}{24} \) into the equation to find the corresponding \( y \)-value: \[ y = 12\left(\frac{5}{24}\right)^2 - 5\left(\frac{5}{24}\right) - 72 \] Simplifying this will give the value of \( y \) at the turning point.