Detailed Notes on Functions

1. Definition of a Function

What is a Function?

• A function is a relation between a set of inputs (the domain) and a set of possible outputs (the range) where each input is related to exactly one output.
• In function notation, if \( f \) is a function and \( x \) is an element of its domain, then \( f(x) \) denotes the output corresponding to \( x \). This is read as "f of x".

Example:

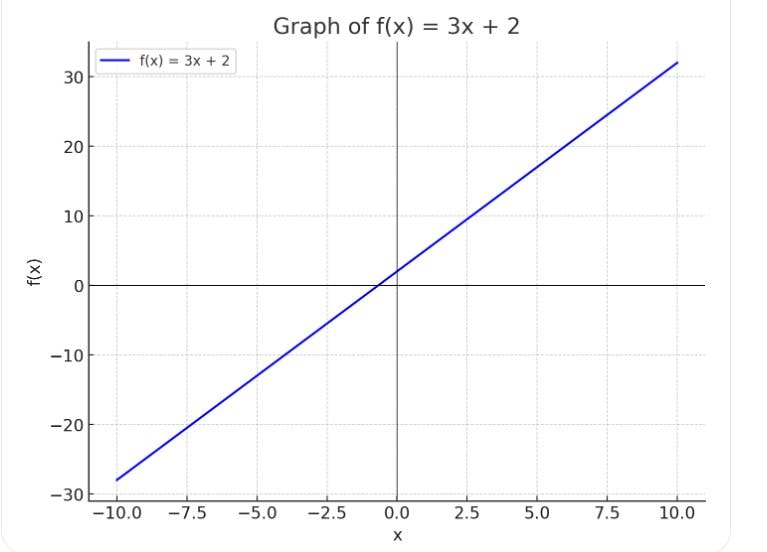
• Let \( f(x) = 3x + 2 \). This is a function that assigns to each value of \( x \) the value \( 3x + 2 \).
• For example, if \( x = 1 \), then \( f(1) = 3(1) + 2 = 5 \).
  

2. Types of Functions by Form

(i) Linear Function:

• A linear function is of the form \( f(x) = ax + b \), where \( a \) and \( b \) are constants.
• The graph of a linear function is a straight line.

Example:

• Let \( f(x) = 3x + 2 \). The function is linear, and its graph is a straight line with slope \( 3 \) and y-intercept \( 2 \).

(ii) Quadratic Function:

• A quadratic function is of the form \( f(x) = ax^2 + bx + c \), where \( a \), \( b \), and \( c \) are constants and \( a \neq 0 \).
• The graph of a quadratic function is a parabola.

Example:

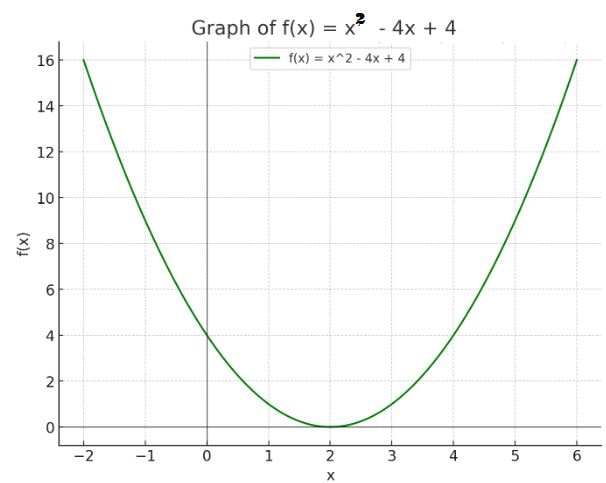
• Let \( f(x) = x^2 - 4x + 4 \). This is a quadratic function, and its graph is a parabola that opens upwards.
• The vertex of the parabola is at \( (2, 0) \).
  

(iii) Polynomial Function:

• A polynomial function is a function that is a sum of terms, each of which is a constant times a non-negative integer power of \( x \).
• The general form is \( f(x) = a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0 \), where \( a_n, a_{n-1}, \dots, a_0 \) are constants.

Example:

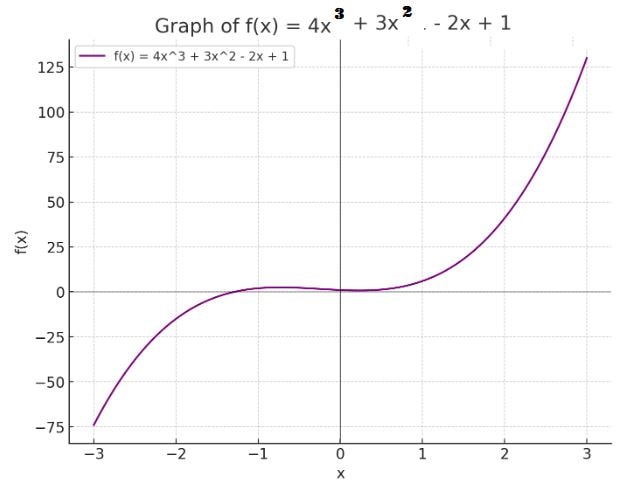
• Let \( f(x) = 4x^3 + 3x^2 - 2x + 1 \). This is a polynomial function of degree 3.
  

(iv) Rational Function:

• A rational function is a function of the form \( f(x) = \frac{p(x)}{q(x)} \), where \( p(x) \) and \( q(x) \) are polynomials and \( q(x) \neq 0 \).

Example:

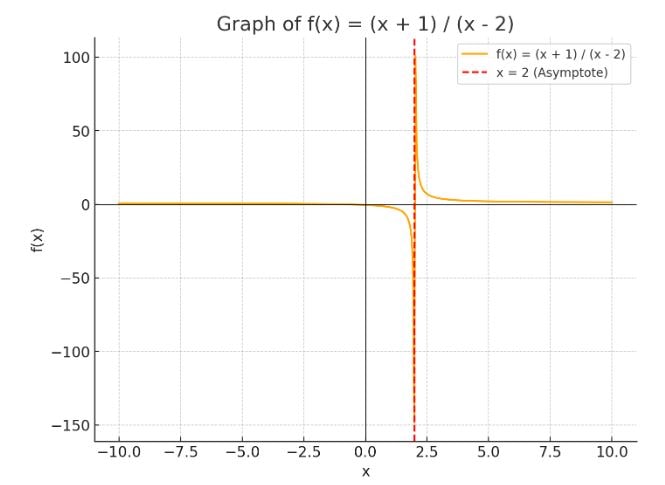
• Let \( f(x) = \frac{x + 1}{x - 2} \). This is a rational function.
• The function has a vertical asymptote at \( x = 2 \) where the denominator equals zero.
  

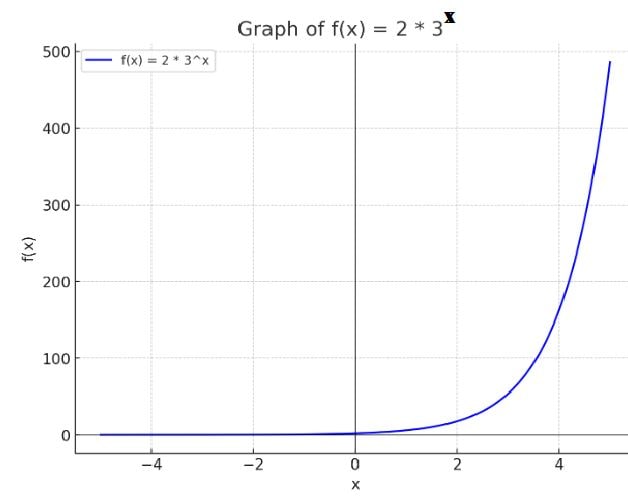
(v) Exponential Function:

• An exponential function is of the form \( f(x) = a \cdot b^x \), where \( a \) and \( b \) are constants, and \( b \) is the base of the exponential.
• The graph of an exponential function shows exponential growth or decay.

Example:

• Let \( f(x) = 2 \cdot 3^x \). This is an exponential function showing exponential growth with base \( 3 \).
  

(vi) Logarithmic Function:

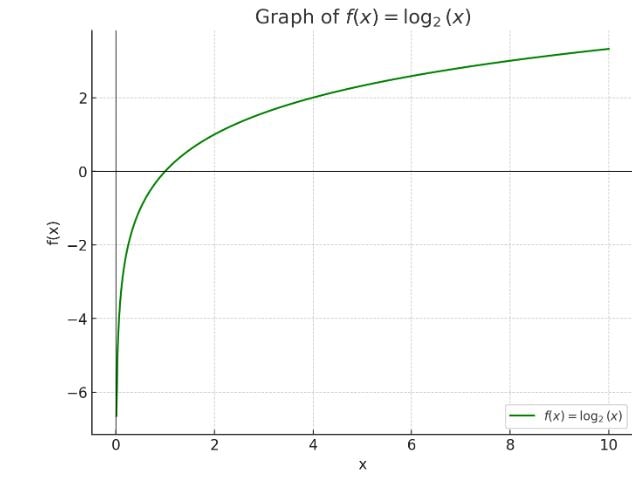
• A logarithmic function is the inverse of an exponential function. It is of the form \( f(x) = \log_b(x) \), where \( b \) is the base of the logarithm.

Example:

• Let \( f(x) = \log_2(x) \). This is a logarithmic function with base \( 2 \).
• The function is undefined for \( x \leq 0 \).
  

(vii) Trigonometric Function:

• Trigonometric functions are functions that relate angles to the ratios of the sides of a right triangle.
• The most common trigonometric functions are sine \( \sin(x) \), cosine \( \cos(x) \), and tangent \( \tan(x) \).
  

Example:

• Let \( f(x) = \sin(x) \). This is a trigonometric function that gives the sine of the angle \( x \).

3. Composite Functions

(i) Composite functions are formed when one function is applied to the result of another function. The notation is \( (f \circ g)(x) = f(g(x)) \).

Solution:

• Let \( f(x) = 2x + 3 \) and \( g(x) = x^2 \). The composite function \( (f \circ g)(x) \) is: \[ (f \circ g)(x) = f(g(x)) = f(x^2) = 2(x^2) + 3 = 2x^2 + 3 \]

4. Inverse Functions

(i) An inverse function reverses the effect of the original function. If \( f(x) \) maps \( x \) to \( y \), then the inverse function, denoted by \( f^{-1}(x) \), maps \( y \) back to \( x \).

Solution:

• To find the inverse of a function, solve for \( x \) in terms of \( y \), then interchange \( x \) and \( y \).
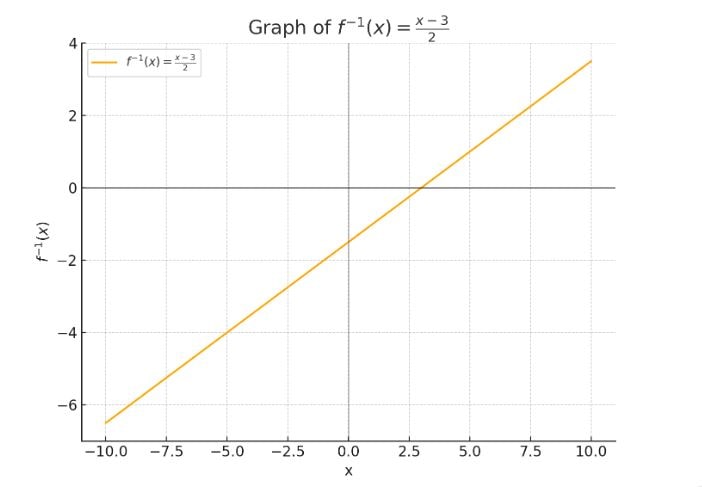
• Example: Find the inverse of \( f(x) = 2x + 3 \): \[ y = 2x + 3 \quad \Rightarrow \quad y - 3 = 2x \quad \Rightarrow \quad x = \frac{y - 3}{2} \] Thus, the inverse function is \( f^{-1}(x) = \frac{x - 3}{2} \).
  

1. One-to-One (Injective) Function

Definition:

• A function \( f \) is called a one-to-one (or injective) function if every element of the domain maps to a unique element of the codomain. This means no two different inputs have the same output.

Example:

• Let \( f(x) = 2x + 3 \). This is a one-to-one function because for each different \( x \) in the domain, the output \( f(x) \) is different.
• If \( f(x_1) = f(x_2) \), then: \[ 2x_1 + 3 = 2x_2 + 3 \quad \Rightarrow \quad x_1 = x_2 \] Therefore, the function is injective.

2. Onto (Surjective) Function

Definition:

• A function \( f \) is called an onto (or surjective) function if every element of the codomain has at least one preimage in the domain. This means the range of the function is equal to the codomain.

Example:

• Let \( f(x) = x^2 \), where the codomain is \( \mathbb{R}_{\geq 0} \) (the set of non-negative real numbers). This function is onto because every non-negative real number has at least one preimage in the domain (either positive or negative values of \( x \)).

3. One-to-Many Function

Definition:

• A relation is called one-to-many if a single input in the domain is related to multiple outputs in the codomain. However, **this is not a valid function** because a function must map each input to exactly one output.

Example:

• A relation where \( f(x) = \{3, 4\} \) for \( x = 2 \). This is not a function because one input is mapping to multiple outputs (3 and 4).

4. Many-to-One Function

Definition:

• A function \( f \) is called a many-to-one function if multiple elements of the domain map to the same element in the codomain. In other words, different inputs can have the same output.

Example:

• Let \( f(x) = x^2 \), where the domain is \( \mathbb{R} \) (the set of real numbers). This is a many-to-one function because both \( f(2) = 4 \) and \( f(-2) = 4 \). Multiple inputs map to the same output.

5. Bijective Function (One-to-One and Onto)

Definition:

• A function is called bijective if it is both injective (one-to-one) and surjective (onto). This means every element of the domain maps to a unique element in the codomain, and every element of the codomain is mapped by some element in the domain.

Example:

• Let \( f(x) = x + 1 \), where both the domain and codomain are \( \mathbb{R} \) (the set of real numbers). This function is bijective because it is both one-to-one and onto.

Examples

1. Injective Function (One-to-One)

Definition:

• A function \( f \) is called injective (or one-to-one) if every element of the domain maps to a unique element in the codomain. No two different inputs have the same output.

Example:

• Let \( f(x) = 2x \), where the domain is \( \mathbb{R} \) (the set of real numbers). This function is injective because every input \( x \) produces a unique output \( 2x \).

2. Surjective Function (Onto)

Definition:

• A function is called surjective (or onto) if every element of the codomain is mapped by some element in the domain. In other words, the function covers the entire codomain.

Example:

• Let \( f(x) = x^2 \), where the domain is \( \mathbb{R} \) and the codomain is \( \mathbb{R}^+ \) (the set of non-negative real numbers). This is surjective because every non-negative real number is the square of some real number.

3. Many-to-One Function

Definition:

• A function \( f \) is called a many-to-one function if multiple elements of the domain map to the same element in the codomain. In other words, different inputs can have the same output.

Example:

• Let \( f(x) = x^2 \), where the domain is \( \mathbb{R} \) (the set of real numbers). This is a many-to-one function because both \( f(2) = 4 \) and \( f(-2) = 4 \). Multiple inputs map to the same output.

4. Bijective Function (One-to-One and Onto)

Definition:

• A function is called bijective if it is both injective (one-to-one) and surjective (onto). This means every element of the domain maps to a unique element in the codomain, and every element of the codomain is mapped by some element in the domain.

Example:

• Let \( f(x) = x + 1 \), where both the domain and codomain are \( \mathbb{R} \) (the set of real numbers). This function is bijective because it is both one-to-one and onto.

Summary of Function Types

• One-to-One (Injective): Each input maps to a unique output.
• Onto (Surjective): Every element of the codomain has a preimage.
• One-to-Many: Not a valid function (one input maps to multiple outputs).
• Many-to-One: Multiple inputs can have the same output.
• Bijective: Both injective and surjective (one-to-one and onto).

Problem 1: Write down the domain of the function f: \( f(x) = 5 - 2x \)

Solution:

• The domain refers to all possible input values for the function. Since it is specified that \( x \in [-4, 5] \), the domain is the closed interval from -4 to 5, inclusive.

Answer:

• The domain of the function is \( [-4, 5] \).

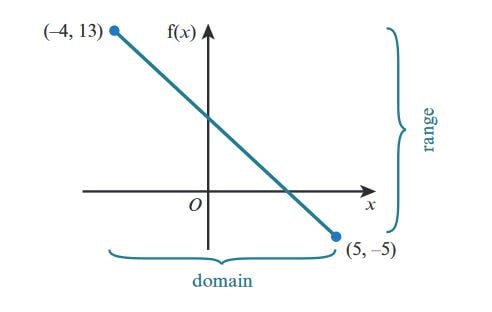
b. Sketch the graph of the function f.

Solution:

• The function \( f(x) = 5 - 2x \) is a linear function. Its slope is -2 and its y-intercept is 5.
• Find key points on the graph:
• At \( x = -4 \), \( f(-4) = 13 \).
• At \( x = 0 \), \( f(0) = 5 \) (the y-intercept).
• At \( x = 5 \), \( f(5) = -5 \).
• The line passes through the points \( (-4, 13) \), \( (0, 5) \), and \( (5, -5) \). This forms a straight line.

Graph:

• Below is the sketch of the graph:

c. Write down the range of the function f.

Solution:

• The range refers to all possible output values for the function.
• From the graph and calculations:
• When \( x = -4 \), \( f(x) = 13 \).
• When \( x = 5 \), \( f(x) = -5 \).
• Since the function is linear, the output values range from -5 to 13 as \( x \) moves from -4 to 5.

Answer:

• The range of the function is \( [-5, 13] \).

Problem 2

a. \( y = 2x - 3 \) for \( x \in \mathbb{R} \)

Solution:

• This is a linear equation of the form \( y = mx + c \), where \( m = 2 \) and \( c = -3 \).
• A linear equation always represents a function because, for each value of \( x \), there is exactly one corresponding value of \( y \).
• Since no two different values of \( x \) produce the same value of \( y \), this is an injective (one-to-one) function.

Answer:

• This is a function, and it is a one-to-one function.

Problem 3

b. \( y = x^2 - 3 \) for \( x \in \mathbb{R} \)

Solution:

• This is a quadratic equation, which forms a parabola when graphed.
• Quadratic equations represent functions because, for each value of \( x \), there is only one value of \( y \).
• However, this is a many-to-one function because different values of \( x \) can produce the same value of \( y \). For example, \( y(-2) = y(2) = 1 \).

Answer:

• This is a function, and it is a many-to-one function.

Problem 4

c. \( y = 2x^3 - 1 \) for \( x \in \mathbb{R} \)

Solution:

• This is a cubic function, which is also a polynomial of degree 3.
• Cubic functions always represent functions because, for each value of \( x \), there is a unique corresponding value of \( y \).
• This is a one-to-one function because different values of \( x \) will produce different values of \( y \) (no two different \( x \) values produce the same \( y \) value).

Answer:

• This is a function, and it is a one-to-one function.

Problem 5

d. \( y = 2^x \) for \( x \in \mathbb{R} \)

Solution:

• This is an exponential function, which always produces a unique value of \( y \) for each value of \( x \).
• Exponential functions represent one-to-one functions because different values of \( x \) always produce different values of \( y \).

Answer:

• This is a function, and it is a one-to-one function.

Problem 6

e. \( y = \frac{10}{x} \) for \( x \in \mathbb{R}, x > 0 \)

Solution:

• This is a rational function, which is defined for \( x > 0 \). For each value of \( x \), there is a unique corresponding value of \( y \).
• Because no two different values of \( x \) produce the same value of \( y \), this is a one-to-one function.

Answer:

• This is a function, and it is a one-to-one function.

Problem 7

f. \( y = 3x^2 + 4 \) for \( x \in \mathbb{R}, x \geq 0 \)

Solution:

• This is another quadratic equation (a parabola), but it is restricted to \( x \geq 0 \). This still produces a unique value of \( y \) for each value of \( x \).
• Because different values of \( x \) can produce the same value of \( y \), this is a many-to-one function. For example, \( y(2) = y(-2) = 16 \).

Answer:

• This is a function, and it is a many-to-one function.

Problem 8:

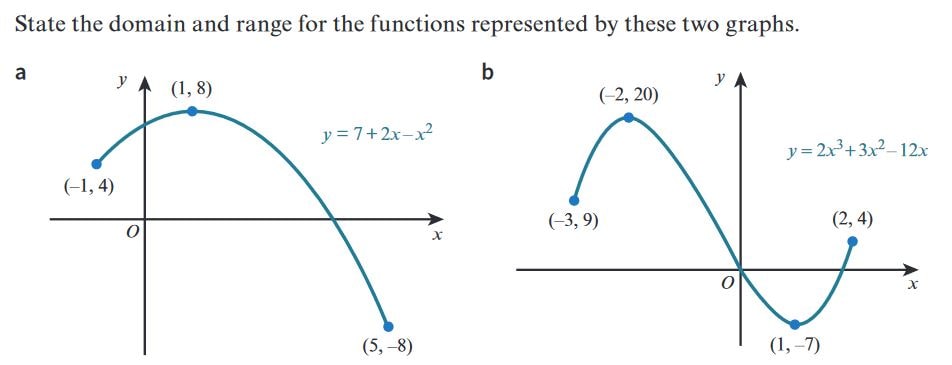
a. State the domain and range of the function represented by the graph.

Solution:

• The graph of the function appears to be a downward-opening parabola, with the equation \( y = 7 + 2x - x^2 \).
• From the graph, we can see the x-values span from \( x = -1 \) to \( x = 5 \).
• The domain is the set of all possible x-values for which the function is defined. Therefore, the domain is \( [-1, 5] \).
• The range is the set of all possible y-values. From the graph, the maximum y-value is 8 (at the vertex \( (1, 8) \)), and the minimum y-value is -8 (at \( (5, -8) \)).

Answer:

• The domain of the function is \( [-1, 5] \).
• The range of the function is \( [-8, 8] \).

b. State the domain and range of the function represented by the graph.

Solution:

• The graph of the function appears to be a cubic function, with the equation \( y = 2x^3 + 3x^2 - 12x \).
• The domain of a cubic function is all real numbers because the function is continuous for all values of x. However, the graph is restricted between the x-values of \( x = -3 \) and \( x = 2 \).
• Thus, the domain of the graph is \( [-3, 2] \).
• The range is the set of all possible y-values. From the graph, the maximum y-value is 20 (at \( (-2, 20) \)), and the minimum y-value is -7 (at \( (1, -7) \)).

Answer:

• The domain of the function is \( [-3, 2] \).
• The range of the function is \( [-7, 20] \).

Problem 9:

11. Find the range of \( f(x) = x^2 + 6x + k \) in terms of \( k \).

Solution:

• The function \( f(x) = x^2 + 6x + k \) is a quadratic function in the form \( ax^2 + bx + c \), where \( a = 1 \), \( b = 6 \), and \( c = k \).
• Since the coefficient of \( x^2 \) (which is 1) is positive, the parabola opens upwards. This means the function has a minimum value at its vertex.
• We find the x-coordinate of the vertex using the formula \( x = -\frac{b}{2a} \):
• For \( f(x) = x^2 + 6x + k \), \( x = -\frac{6}{2(1)} = -3 \).
• Substitute \( x = -3 \) back into the function to find the minimum value of \( f(x) \):
• \( f(-3) = (-3)^2 + 6(-3) + k = 9 - 18 + k = -9 + k \).
• Therefore, the minimum value of \( f(x) \) is \( -9 + k \).
• Since the parabola opens upwards, the range of \( f(x) \) is all values greater than or equal to \( -9 + k \).

Answer:

• The range of \( f(x) \) is \( [ -9 + k, \infty ) \).

12. Find the range of \( g(x) = 5 - ax - 2x^2 \) in terms of \( a \).

Solution:

• The function \( g(x) = 5 - ax - 2x^2 \) is a quadratic function in the form \( ax^2 + bx + c \), where \( a = -2 \), \( b = -a \), and \( c = 5 \).
• Since the coefficient of \( x^2 \) (which is -2) is negative, the parabola opens downwards. This means the function has a maximum value at its vertex.
• We find the x-coordinate of the vertex using the formula \( x = -\frac{b}{2a} \):
• For \( g(x) = 5 - ax - 2x^2 \), \( x = -\frac{-a}{2(-2)} = \frac{a}{4} \).
• Substitute \( x = \frac{a}{4} \) back into the function to find the maximum value of \( g(x) \):
• \( g\left(\frac{a}{4}\right) = 5 - a\left(\frac{a}{4}\right) - 2\left(\frac{a}{4}\right)^2 = 5 - \frac{a^2}{4} - 2\left(\frac{a^2}{16}\right) \).
• Simplifying further, \( g\left(\frac{a}{4}\right) = 5 - \frac{a^2}{4} - \frac{a^2}{8} = 5 - \frac{2a^2}{8} - \frac{a^2}{8} = 5 - \frac{3a^2}{8} \).
• Therefore, the maximum value of \( g(x) \) is \( 5 - \frac{3a^2}{8} \).
• Since the parabola opens downwards, the range of \( g(x) \) is all values less than or equal to \( 5 - \frac{3a^2}{8} \).

Answer:

• The range of \( g(x) \) is \( \left( -\infty, 5 - \frac{3a^2}{8} \right] \).

Find the Domain and Range of these functions

• 1) \( f(x) = x^2 - 2 \) for \( x \in \mathbb{R} \)
• 2) \( f : x \mapsto x^2 + 3 \) for \( -2 \leq x \leq 5 \)
• 3) \( f(x) = 3 - 2x^2 \) for \( x \leq 2 \)
• 4) \( f(x) = 7 - 3x^2 \) for \( -1 \leq x \leq 2 \)
• 5) \( f(x) = x^2 - 2x - 3 \) for \( x \in \mathbb{R}, -a \leq x \leq a \)
• 6) If the range of the function \( f \) is \( -4 \leq f(x) \leq 5 \), find the value of \( a \).
• 7) \( f(x) = x^2 + x - 4 \) for \( x \in \mathbb{R}, a \leq x \leq a + 3 \)
• 8) If the range of the function \( f \) is \( -2 \leq f(x) \leq 16 \), find the possible values of \( a \).

Algebra Worksheet

Name: __________________________ Date: __________________________

Instructions:

Solve the following equations and find the real roots. Provide your final answer in the space provided.

Questions:

1) Find the real roots of the equation:

• \( \frac{9}{x^4} + \frac{8}{x^2} = 1 \)

Answer: _______________________

2) Solve:

• \( x^4 - 13x^2 + 36 = 0 \)

Answer: _______________________

3) Find the real roots of the equation:

• \( x^2 - 2 = \frac{8}{x^2} \)

Answer: _______________________

4) Solve:

• \( x^6 - 7x^3 - 8 = 0 \)

Answer: _______________________

5) Solve:

• \( 2x^4 - 11x^2 + 5 = 0 \)

Answer: _______________________

6) Solve the equation:

• \( \frac{9}{x^4} + \frac{5}{x^2} = 4 \)

Answer: _______________________

7) Solve:

• \( 2x - 9\sqrt{x} + 10 = 0 \)

Answer: _______________________

8) Solve:

• \( \sqrt{x}(\sqrt{x} + 1) = 6 \)

Answer: _______________________

9) Find the x-coordinates of points A and B where the curve \( y = 2\sqrt{x} \) and the line \( 3y = x + 8 \) intersect.

Answer: _______________________

10) Find the values of \( a \), \( b \), and \( c \) for the quadratic equation \( y = ax^2 + bx + c \), given that the graph crosses the x-axis at \( (1, 0) \) and \( \left(\frac{49}{4}, 0\right) \) and meets the y-axis at \( (0, 7) \).

Answer: \( a = __________, b = __________, c = __________ \)

Answer Key:

• 1) \( x = 3 \) or \( x = -3 \)
• 2) \( x = \pm 3 \) or \( x = \pm 2 \)
• 3) \( x = 2 \) or \( x = -2 \)
• 4) \( x = 2 \) or \( x = -1 \)
• 5) \( x = \pm \sqrt{5} \) or \( x = \pm \frac{\sqrt{2}}{2} \)
• 6) \( x = \frac{3}{2} \) or \( x = -\frac{3}{2} \)
• 7) \( x = 6.25 \) or \( x = 4 \)
• 8) \( x = 4 \)
• 9) \( x = 16 \) and \( x = 4 \)
• 10) \( a = \frac{4}{7}, b = -\frac{53}{7}, c = 7 \)

Find the Domain and Range Worksheet

Name: __________________________ Date: __________________________

Instructions:

Find the domain and range of the following functions. Provide your final answer in the space provided.

Questions:

1) Find the domain and range of the function:

• \( f(x) = x^2 - 2 \) for \( x \in \mathbb{R} \)

Domain: _______________________

Range: _______________________

2) Find the domain and range of the function:

• \( f(x) = x^2 + 3 \) for \( -2 \leq x \leq 5 \)

Domain: _______________________

Range: _______________________

3) Find the domain and range of the function:

• \( f(x) = 3 - 2x^2 \) for \( x \leq 2 \)

Domain: _______________________

Range: _______________________

4) Find the domain and range of the function:

• \( f(x) = 7 - 3x^2 \) for \( -1 \leq x \leq 2 \)

Domain: _______________________

Range: _______________________

5) Find the domain and range of the function:

• \( f(x) = x^2 - 2x - 3 \) for \( x \in \mathbb{R}, -a \leq x \leq a \)

Domain: _______________________

Range: _______________________

6) If the range of the function \( f \) is \( -4 \leq f(x) \leq 5 \), find the value of \( a \).

Answer: _______________________

7) Find the domain and range of the function:

• \( f(x) = x^2 + x - 4 \) for \( x \in \mathbb{R}, a \leq x \leq a + 3 \)

Domain: _______________________

Range: _______________________

8) If the range of the function \( f \) is \( -2 \leq f(x) \leq 16 \), find the possible values of \( a \).

Answer: _______________________

Answer Key:

• 1) Domain: \( \mathbb{R} \), Range: \( [-2, \infty) \)


• 2) Domain: \( [-2, 5] \), Range: \( [3, 28] \)


• 3) Domain: \( (-\infty, 2] \), Range: \( (-\infty, -5] \)


• 4) Domain: \( [-1, 2] \), Range: \( [-5, 7] \)


• 5) Domain: \( [-a, a] \), Range: \( [-4, 5] \)


• 6) \( a = 2 \)


• 7) Domain: \( [a, a+3] \), Range: \( [-2, 16] \)


• 8) Possible values of \( a \): \( a = -1 \) or \( a = 2 \)

Definition:

Composite Function: A composite function is formed when one function is applied to the result of another function. For example, if you have two functions \( f(x) \) and \( g(x) \), the composite function \( g(f(x)) \) means you first apply \( f(x) \), then apply \( g(x) \) to the result of \( f(x) \). Mathematically, \( g(f(x)) \) is obtained by substituting \( f(x) \) into the equation for \( g(x) \).

Example Problem:

Given:

• \( f(x) = 2x - 5 \) for \( x \in \mathbb{R} \)
• \( g(x) = 3x - 1 \) for \( x \in \mathbb{R} \)

Find the composite function \( g(f(x)) \).

Steps:

Step 1: Write down the expression for \( f(x) \) and \( g(x) \).

• \( f(x) = 2x - 5 \)
• \( g(x) = 3x - 1 \)

Step 2: Substitute \( f(x) \) into \( g(x) \).

• Since \( g(x) = 3x - 1 \), replace \( x \) in \( g(x) \) with \( f(x) \).
• This gives: \( g(f(x)) = 3(2x - 5) - 1 \).

Step 3: Simplify the expression.

• Distribute the 3: \( g(f(x)) = 3(2x - 5) - 1 = 6x - 15 - 1 \).
• Combine like terms: \( g(f(x)) = 6x - 16 \).

Answer:

The composite function is:

• \( g(f(x)) = 6x - 16 \)

Summary:

The composite function \( g(f(x)) \) is obtained by substituting the expression for \( f(x) \) into \( g(x) \), then simplifying the resulting expression.

Worked Example:

Follow the steps below to find \( f(g(4)) \).

Problem:

• \( f(x) = (x - 4)^2 - 1 \) for \( x \in \mathbb{R} \)
• \( g(x) = \frac{2x + 3}{x - 2} \) for \( x \in \mathbb{R}, x > 2 \)

Find \( f(g(4)) \).

Steps:

Step 1: Find the value of \( g(4) \).

• Use the function \( g(x) = \frac{2x + 3}{x - 2} \).
• Substitute \( x = 4 \) into \( g(x) \):
• \( g(4) = \frac{2(4) + 3}{4 - 2} = \frac{8 + 3}{2} = \frac{11}{2} \).

Step 2: Find \( f(g(4)) \) by substituting \( g(4) \) into the function \( f(x) \).

• Use the function \( f(x) = (x - 4)^2 - 1 \).
• Substitute \( g(4) = \frac{11}{2} \) into \( f(x) \):
• \( f\left(\frac{11}{2}\right) = \left(\frac{11}{2} - 4\right)^2 - 1 \).
• Simplify inside the parentheses: \( \frac{11}{2} - 4 = \frac{11}{2} - \frac{8}{2} = \frac{3}{2} \).
• Now, square \( \frac{3}{2} \): \( \left(\frac{3}{2}\right)^2 = \frac{9}{4} \).
• Subtract 1: \( f\left(\frac{11}{2}\right) = \frac{9}{4} - 1 = \frac{9}{4} - \frac{4}{4} = \frac{5}{4} \).

Instructions:

Follow the steps below to find \( f(g(4)) \).

Problem:

• \( f(x) = (x - 4)^2 - 1 \) for \( x \in \mathbb{R} \)
• \( g(x) = \frac{2x + 3}{x - 2} \) for \( x \in \mathbb{R}, x > 2 \)

Find \( f(g(4)) \).

Steps:

Step 1: Find the value of \( g(4) \).

• Use the function \( g(x) = \frac{2x + 3}{x - 2} \).
• Substitute \( x = 4 \) into \( g(x) \):
• \( g(4) = \frac{2(4) + 3}{4 - 2} = \frac{8 + 3}{2} = \frac{11}{2} \).

Step 2: Find \( f(g(4)) \) by substituting \( g(4) \) into the function \( f(x) \).

• Use the function \( f(x) = (x - 4)^2 - 1 \).
• Substitute \( g(4) = \frac{11}{2} \) into \( f(x) \):
• \( f\left(\frac{11}{2}\right) = \left(\frac{11}{2} - 4\right)^2 - 1 \).
• Simplify inside the parentheses: \( \frac{11}{2} - 4 = \frac{11}{2} - \frac{8}{2} = \frac{3}{2} \).
• Now, square \( \frac{3}{2} \): \( \left(\frac{3}{2}\right)^2 = \frac{9}{4} \).
• Subtract 1: \( f\left(\frac{11}{2}\right) = \frac{9}{4} - 1 = \frac{9}{4} - \frac{4}{4} = \frac{5}{4} \).

Answer:

The value of \( f(g(4)) \) is:

• \( f(g(4)) = \frac{5}{4} \).

Summary:

To find \( f(g(4)) \), we first evaluated \( g(4) \), then substituted this value into the function \( f(x) \), and simplified to obtain the final answer.

Problem:

Instructions:

Find the values of \( k \) for which the equation \( f(g(x)) = k \) has real solutions by following the steps below.

Problem:

• \( f(x) = x^2 + 4x \) for \( x \in \mathbb{R} \)


• \( g(x) = 3x - 1 \) for \( x \in \mathbb{R} \)

Find the values of \( k \) for which the equation \( f(g(x)) = k \) has real solutions.

Steps:

Step 1: Find the expression for \( f(g(x)) \).

• Start by substituting \( g(x) = 3x - 1 \) into \( f(x) \).
• \( f(g(x)) = f(3x - 1) \).
• Use the function \( f(x) = x^2 + 4x \), so:
• \( f(g(x)) = (3x - 1)^2 + 4(3x - 1) \).

Step 2: Expand the expression for \( f(g(x)) \).

• Expand \( (3x - 1)^2 = 9x^2 - 6x + 1 \).
• Expand \( 4(3x - 1) = 12x - 4 \).
• Therefore, \( f(g(x)) = 9x^2 - 6x + 1 + 12x - 4 = 9x^2 + 6x - 3 \).

Step 3: Set up the equation \( f(g(x)) = k \) and solve for real solutions.

• The equation becomes \( 9x^2 + 6x - 3 = k \).
• Rearrange this to \( 9x^2 + 6x - (k + 3) = 0 \), which is a quadratic equation.

Step 4: Use the discriminant to determine when the quadratic has real solutions.

• The discriminant of a quadratic equation \( ax^2 + bx + c = 0 \) is \( \Delta = b^2 - 4ac \).
• In our case, \( a = 9 \), \( b = 6 \), and \( c = -(k + 3) \).
• The discriminant is \( \Delta = 6^2 - 4(9)(-(k + 3)) = 36 + 36(k + 3) = 36k + 144 \).

Step 5: Set the discriminant \( \Delta \geq 0 \) for real solutions.

• For real solutions, the discriminant must be non-negative: \( 36k + 144 \geq 0 \).


• Solve for \( k \): \( 36k \geq -144 \), so \( k \geq -4 \).

Answer:

The values of \( k \) for which the equation \( f(g(x)) = k \) has real solutions are:

• \( k \geq -4 \).

Summary:

We found that the quadratic equation resulting from \( f(g(x)) = k \) will have real solutions when the discriminant is non-negative. Solving this inequality, we determined that \( k \) must be greater than or equal to -4 for real solutions to exist.

Composite Functions Worksheet

Name: __________________________ Date: __________________________

Instructions:

Find the composite functions for the following problems. Show your work and provide your final answer in the space provided.

Questions:

1) Given \( f(x) = 2x + 3 \) and \( g(x) = x^2 - 1 \), find \( f(g(2)) \).

Answer: _______________________

2) Given \( f(x) = x^2 + 2x \) and \( g(x) = 3x - 4 \), find \( f(g(x)) \).

Answer: _______________________

3) Given \( f(x) = 4x - 1 \) and \( g(x) = \frac{x}{2} + 5 \), find \( g(f(x)) \).

Answer: _______________________

4) Let \( f(x) = \sqrt{x + 2} \) and \( g(x) = 2x^2 - 3 \). Find \( f(g(1)) \).

Answer: _______________________

5) Let \( f(x) = 3x + 1 \) and \( g(x) = x^3 - 2 \). Find \( g(f(2)) \).

Answer: _______________________

6) Given \( f(x) = 5x - 7 \) and \( g(x) = \frac{2x}{3} \), find \( f(g(x)) \).

Answer: _______________________

7) Let \( f(x) = x^2 + 3x \) and \( g(x) = \sqrt{x - 1} \). Find \( f(g(4)) \).

Answer: _______________________

8) Let \( f(x) = 2x^3 + 1 \) and \( g(x) = x - 4 \). Find \( f(g(x)) \).

Answer: _______________________

9) Given \( f(x) = 6x + 5 \) and \( g(x) = \frac{x - 3}{2} \), find \( g(f(1)) \).

Answer: _______________________

10) Let \( f(x) = \frac{1}{x} \) and \( g(x) = 4x - 7 \). Find \( f(g(3)) \).

Answer: _______________________

Answer Key:

• 1) \( f(g(2)) = 11 \)
• 2) \( f(g(x)) = 9x^2 - 24x + 14 \)
• 3) \( g(f(x)) = 2x + 5 \)
• 4) \( f(g(1)) = 1 \)
• 5) \( g(f(2)) = 23 \)
• 6) \( f(g(x)) = \frac{10x}{3} - 7 \)
• 7) \( f(g(4)) = 15 \)
• 8) \( f(g(x)) = 2(x - 4)^3 + 1 \)
• 9) \( g(f(1)) = 4 \)
• 10) \( f(g(3)) = \frac{1}{5} \)

Inverse Functions Worksheet

Name: __________________________ Date: __________________________

Instructions:

Find the inverse of the following functions. Show your work and provide your final answer in the space provided.

Questions:

1) Find the inverse of the function \( f(x) = 2x + 5 \).

Answer: _______________________

2) Find the inverse of the function \( f(x) = \frac{x - 3}{4} \).

Answer: _______________________

3) Find the inverse of the function \( f(x) = x^2 - 1 \) for \( x \geq 0 \).

Answer: _______________________

4) Find the inverse of the function \( f(x) = \frac{1}{x} \).

Answer: _______________________

5) Find the inverse of the function \( f(x) = 3x^2 + 2 \) for \( x \geq 0 \).

Answer: _______________________

6) Find the inverse of the function \( f(x) = \sqrt{x + 7} \).

Answer: _______________________

7) Find the inverse of the function \( f(x) = 4x - 9 \).

Answer: _______________________

8) Find the inverse of the function \( f(x) = \frac{2x + 1}{x - 2} \).

Answer: _______________________

9) Find the inverse of the function \( f(x) = \ln(x) \).

Answer: _______________________

10) Find the inverse of the function \( f(x) = e^x \).

Answer: _______________________

Answer Key:

• 1) \( f^{-1}(x) = \frac{x - 5}{2} \)
• 2) \( f^{-1}(x) = 4x + 3 \)
• 3) \( f^{-1}(x) = \sqrt{x + 1} \)
• 4) \( f^{-1}(x) = \frac{1}{x} \)
• 5) \( f^{-1}(x) = \frac{\sqrt{x - 2}}{3} \)
• 6) \( f^{-1}(x) = x^2 - 7 \)
• 7) \( f^{-1}(x) = \frac{x + 9}{4} \)
• 8) \( f^{-1}(x) = \frac{2x - 1}{x - 1} \)
• 9) \( f^{-1}(x) = e^x \)
• 10) \( f^{-1}(x) = \ln(x) \)

Problem:

• \( f(x) = (2x - 1)^3 - 3 \) for \( x \in \mathbb{R}, 1 \leq x \leq 3 \)

a) Find an expression for \( f^{-1}(x) \).

Steps:

Step 1: Start by setting \( y = f(x) \).

• \( y = (2x - 1)^3 - 3 \)

Step 2: Solve for \( x \) in terms of \( y \).

• \( y + 3 = (2x - 1)^3 \)
• Take the cube root: \( \sqrt[3]{y + 3} = 2x - 1 \)
• Solve for \( x \): \( x = \frac{\sqrt[3]{y + 3} + 1}{2} \)

Answer:

\( f^{-1}(x) = \frac{\sqrt[3]{x + 3} + 1}{2} \).

b) Find the domain of \( f^{-1} \).

Steps:

Step 1: The range of the original function \( f(x) \) determines the domain of \( f^{-1}(x) \).

• The range of \( f(x) \) for \( 1 \leq x \leq 3 \) is obtained by evaluating the function at the endpoints.
• \( f(1) = -2 \) and \( f(3) = 13 \).

Answer:

The domain of \( f^{-1}(x) \) is \( [-2, 13] \).

Problem:

• \( f(x) = x^2 - 10x \) for \( x \in \mathbb{R}, x \geq 5 \)

a) Express \( f(x) \) in the form \( (x - a)^2 - b \).

Steps:

Step 1: Complete the square.

• Start with \( f(x) = x^2 - 10x \).
• Add and subtract \( \left(\frac{10}{2}\right)^2 = 25 \):
• \( f(x) = (x^2 - 10x + 25) - 25 = (x - 5)^2 - 25 \).

Answer:

\( f(x) = (x - 5)^2 - 25 \).

b) Find an expression for \( f^{-1}(x) \) and state the domain of \( f^{-1} \).

Steps:

Step 1: Set \( y = (x - 5)^2 - 25 \) and solve for \( x \).

• \( y + 25 = (x - 5)^2 \)
• Take the square root: \( \sqrt{y + 25} = x - 5 \)
• Solve for \( x \): \( x = \sqrt{y + 25} + 5 \) (since \( x \geq 5 \), we take the positive root).

Answer:

\( f^{-1}(x) = \sqrt{x + 25} + 5 \).

Domain:

The domain of \( f^{-1}(x) \) is \( [-25, \infty) \).

Problem:

• \( f(x) = \frac{1}{x - 1} \) for \( x \in \mathbb{R}, x \neq 1 \)

a) Find an expression for \( f^{-1}(x) \).

Steps:

Step 1: Set \( y = \frac{1}{x - 1} \) and solve for \( x \).

• \( y(x - 1) = 1 \)
• \( x - 1 = \frac{1}{y} \)
• Solve for \( x \): \( x = \frac{1}{y} + 1 \).

Answer:

\( f^{-1}(x) = \frac{1}{x} + 1 \).

b) Show that if \( f(x) = f^{-1}(x) \), then \( x^2 - x - 1 = 0 \).

Steps:

Step 1: Set \( f(x) = f^{-1}(x) \).

• \( \frac{1}{x - 1} = \frac{1}{x} + 1 \)

Step 2: Cross multiply to eliminate the fractions.

• \( x(x - 1) = 1 \)
• Expand: \( x^2 - x = 1 \)
• Rearrange: \( x^2 - x - 1 = 0 \).

Answer:

The equation \( x^2 - x - 1 = 0 \) is satisfied when \( f(x) = f^{-1}(x) \).

c) Find the values of \( x \) for which \( f(x) = f^{-1}(x) \). Give your answer in surd form.

Steps:

Step 1: Solve the quadratic equation \( x^2 - x - 1 = 0 \).

• Use the quadratic formula: \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \).
• For \( x^2 - x - 1 = 0 \), \( a = 1 \), \( b = -1 \), and \( c = -1 \).
• \( x = \frac{1 \pm \sqrt{1^2 - 4(1)(-1)}}{2(1)} = \frac{1 \pm \sqrt{5}}{2} \).

Answer:

The values of \( x \) are \( x = \frac{1 + \sqrt{5}}{2} \) and \( x = \frac{1 - \sqrt{5}}{2} \).

Problem:

Q1. What type of mapping is this function?

Solution:

• The given function \( f(x) = (x - 2)^2 + 1 \) is a quadratic function.
• Quadratic functions generally have the mapping type "many-to-one," because different values of \( x \) can produce the same \( f(x) \) value.
• Therefore, the function is a "many-to-one" mapping.

Q2. What are the coordinates of the vertex of the parabola?

Solution:

• The function \( f(x) = (x - 2)^2 + 1 \) is written in the vertex form \( f(x) = (x - h)^2 + k \), where \( (h, k) \) are the coordinates of the vertex.
• Here, \( h = 2 \) and \( k = 1 \).
• Thus, the coordinates of the vertex are: \[ (2, 1) \]

Q3. What is the domain of the function?

Solution:

• The domain of a quadratic function is the set of all real numbers, because the function is defined for all \( x \) values.
• Therefore, the domain of the function is: \[ \mathbb{R} \text{ (All real numbers)} \]

Q4. What is the range of the function?

Solution:

• The range of a function is the set of all possible values of \( f(x) \).
• Since \( (x - 2)^2 \geq 0 \), the minimum value of \( (x - 2)^2 + 1 \) is 1, which occurs at the vertex \( (2, 1) \).
• As \( x \) increases or decreases away from 2, \( f(x) \) increases without bound.
• Therefore, the range of the function is: \[ f(x) \geq 1 \quad \text{or} \quad [1, \infty) \]

Q5. Does this function have an inverse?

Solution:

• A function has an inverse if it is one-to-one (injective), meaning each output corresponds to exactly one input.
• Since the given function is a "many-to-one" mapping, it does not have an inverse over the entire domain.

Q6. If \( f \) has an inverse, what is it? If not, then how could you change the domain of \( f \) so that the function does have an inverse?

Solution:

• To make the function one-to-one, we need to restrict the domain so that the function becomes either strictly increasing or strictly decreasing.
• We can restrict the domain to \( x \geq 2 \) or \( x \leq 2 \). Let's choose \( x \geq 2 \).
• With this restricted domain, the function is now one-to-one, and we can find the inverse by solving for \( x \) in terms of \( y \): \[ y = (x - 2)^2 + 1 \] Subtract 1 from both sides: \[ y - 1 = (x - 2)^2 \]
• Take the square root of both sides: \[ \sqrt{y - 1} = x - 2 \]
• Add 2 to both sides to solve for \( x \): \[ x = \sqrt{y - 1} + 2 \]
• Therefore, the inverse function is: \[ f^{-1}(y) = \sqrt{x - 1} + 2 \]
• With the restricted domain \( x \geq 2 \), the inverse function is defined and valid.

Worked Examples

Q1

What was the primary reason for the collapse of the Bronze Age civilizations around 1200 BCE?

Solution:

• The collapse is attributed to a combination of factors, including natural disasters, invasions by the Sea Peoples, internal social upheavals, and a breakdown in trade networks.
• This disrupted the supply of tin and copper necessary for making bronze, leading to the downfall of major civilizations such as the Mycenaeans, Hittites, and Egyptians.

Q2

What is the "Ship of Theseus" paradox, and what does it question about identity?

Solution:

• The "Ship of Theseus" paradox asks whether a ship that has had all its components replaced remains fundamentally the same ship.
• This paradox challenges the concept of identity, questioning whether an object that undergoes gradual change can still be considered the same object.

Q3

What is Gödel's Incompleteness Theorem, and how does it impact mathematical systems?

Solution:

• Gödel's Incompleteness Theorem states that in any consistent mathematical system, there are statements that are true but cannot be proven within that system.
• This means that no mathematical system can be both complete and consistent, implying that some truths will always lie beyond formal proof.

Q4

What is the "Fermi Paradox," and what does it question about extraterrestrial life?

Solution:

• The Fermi Paradox questions why, despite the high probability of extraterrestrial life, we have not yet encountered any evidence of other civilizations.
• This paradox highlights the apparent contradiction between the vastness of the universe and the lack of observational evidence of alien life.

Q5

What is the Sapir-Whorf Hypothesis, and how does it influence our understanding of language and thought?

Solution:

• The Sapir-Whorf Hypothesis posits that the structure of a language influences its speakers' cognition and worldview.
• It suggests that people who speak different languages perceive and think about the world differently because language shapes thought processes.

Q6

What is the "Red Queen Hypothesis," and how does it relate to evolutionary biology?

Solution:

• The Red Queen Hypothesis suggests that organisms must constantly adapt and evolve to survive in an ever-changing environment where other species are also evolving.
• This concept emphasizes continuous evolutionary arms races between species.

Q7

What is the significance of Göbekli Tepe, and how does it challenge traditional views of human civilization?

Solution:

• Göbekli Tepe is significant because it predates the advent of agriculture and permanent settlements.
• This challenges the traditional view that complex societies developed only after the establishment of agriculture and suggests that organized religion and monumental architecture may have preceded farming.

Q8

What is the "Dunning-Kruger Effect," and how does it influence people's perception of their abilities?

Solution:

• The Dunning-Kruger Effect is a cognitive bias in which people with low ability or knowledge overestimate their competence, while those with high competence tend to underestimate their abilities.
• This effect highlights the lack of self-awareness in individuals regarding their own skills.

Q9

What is the "Paradox of Thrift," and how does it relate to macroeconomic theory?

Solution:

• The Paradox of Thrift suggests that while saving money is beneficial for individuals, if everyone saves more during a recession, overall demand will fall, leading to lower total savings and a weaker economy.
• This paradox illustrates the conflict between individual rationality and collective outcomes in economics.

Q10

What is the significance of the "Arnolfini Portrait" by Jan van Eyck, and what are its key symbolic elements?

Solution:

• The "Arnolfini Portrait" is significant for its intricate detail and use of symbolism.
• Key elements include the mirror reflecting the scene, the dog symbolizing loyalty, and the use of light to create depth and realism, often interpreted as a visual contract or depiction of marriage.

• Function: A relationship between two sets in which each element of the first set is associated with exactly one element of the second set. Typically written as \( f(x) \).
• Domain: The set of all possible input values (x-values) for which a function is defined.
• Range: The set of all possible output values (y-values) of a function.
• Composite Function: A function formed by applying one function to the results of another. Denoted as \( (f \circ g)(x) = f(g(x)) \).
• Inverse Function: A function that "reverses" the effect of the original function. If \( f(x) \) maps \( x \) to \( y \), then \( f^{-1}(y) \) maps \( y \) back to \( x \).
• One-to-One Function (Injective): A function where each element of the domain maps to a unique element of the range. No two different inputs have the same output.
• Onto Function (Surjective): A function where every element of the range is mapped by at least one element of the domain. All possible outputs are covered.
• Bijective Function: A function that is both injective (one-to-one) and surjective (onto). It has a one-to-one correspondence between the domain and the range.
• Vertical Line Test: A visual test used to determine if a graph represents a function. If a vertical line intersects the graph at more than one point, it is not a function.
• Horizontal Line Test: A visual test used to determine if a function is injective (one-to-one). If a horizontal line intersects the graph at more than one point, the function is not injective.
• Quadratic Function: A polynomial function of degree 2, generally written as \( f(x) = ax^2 + bx + c \).
• Linear Function: A function of the form \( f(x) = mx + b \), where \( m \) and \( b \) are constants. The graph of a linear function is a straight line.
• Polynomial Function: A function involving terms of the form \( ax^n \), where \( n \) is a non-negative integer and \( a \) is a constant. For example, \( f(x) = x^3 - 2x + 5 \).
• Rational Function: A function that is the ratio of two polynomials, expressed as \( f(x) = \frac{p(x)}{q(x)} \), where \( p(x) \) and \( q(x) \) are polynomials and \( q(x) \neq 0 \).
• Exponential Function: A function of the form \( f(x) = a \cdot b^x \), where \( a \) and \( b \) are constants and \( b > 0 \). The graph shows exponential growth or decay.
• Logarithmic Function: The inverse of an exponential function, generally written as \( f(x) = \log_b(x) \), where \( b \) is the base.
• Absolute Value Function: A function that gives the non-negative value of a number, denoted as \( f(x) = |x| \).
• Piecewise Function: A function defined by multiple sub-functions, each of which applies to a specific interval of the domain.
• Asymptote: A line that a graph approaches but never touches. Asymptotes can be vertical, horizontal, or oblique.
• Critical Points: Points on the graph of a function where the derivative is zero or undefined, indicating a potential maximum, minimum, or inflection point.
• Maximum/Minimum: The highest or lowest point on the graph of a function, respectively. These points occur at critical points where the derivative is zero or changes sign.
• Zero of a Function: A value of \( x \) for which \( f(x) = 0 \). Also called the root of the function.
• Monotonic Function: A function that is either entirely non-increasing or non-decreasing throughout its domain.
• Increasing/Decreasing Function: A function is increasing if the output increases as the input increases, and decreasing if the output decreases as the input increases.
• Transformation: A change made to the graph of a function, such as a translation (shift), reflection, stretching, or compression.
• Symmetry: A property of a function where its graph is a mirror image over a line (axis of symmetry) or a point.
• Parabola: The U-shaped graph of a quadratic function. The vertex of the parabola represents the maximum or minimum point.
• Horizontal Shift: A translation of the graph of a function left or right. For example, \( f(x - c) \) shifts the graph \( c \) units to the right.
• Vertical Shift: A translation of the graph of a function up or down. For example, \( f(x) + c \) shifts the graph \( c \) units upwards.
• Reflection: A flip of the graph of a function over a line, such as the x-axis or y-axis.
• Stretching and Compression: Changes to the graph of a function where it is stretched or compressed vertically or horizontally by a factor.

Algebra Week 2 Teaching Plan

Q1 (Find the Vertex and Axis of Symmetry for \( f(x) = x^2 + 8x - 1 \))

Given: \( f(x) = x^2 + 8x - 1 \)

Solution:

• Complete the square: \[ f(x) = x^2 + 8x + \left(\frac{8}{2}\right)^2 - \left(\frac{8}{2}\right)^2 - 1 = (x + 4)^2 - 17 \]
• The vertex is \( (-4, -17) \).
• The formula for the axis of symmetry is \( x = -\frac{b}{2a} \). For this equation, \( a = 1 \) and \( b = 8 \), so: \[ x = -\frac{8}{2(1)} = -4 \]
• The axis of symmetry is \( x = -4 \).

Q2 (Find the Vertex and Axis of Symmetry for \( f(x) = x^2 + 10x + 25 \))

Given: \( f(x) = x^2 + 10x + 25 \)

Solution:

• Recognize that this is a perfect square: \[ f(x) = (x + 5)^2 \]
• The vertex is \( (-5, 0) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = 1 \) and \( b = 10 \): \[ x = -\frac{10}{2(1)} = -5 \]
• The axis of symmetry is \( x = -5 \).

Q3 (Find the Vertex and Axis of Symmetry for \( f(x) = -x^2 + 2x + 5 \))

Given: \( f(x) = -x^2 + 2x + 5 \)

Solution:

• Factor out the negative sign and complete the square: \[ f(x) = -\left(x^2 - 2x + 1 - 1 + 5\right) = -(x - 1)^2 + 6 \]
• The vertex is \( (1, 6) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -1 \) and \( b = 2 \): \[ x = -\frac{2}{2(-1)} = 1 \]
• The axis of symmetry is \( x = 1 \).

Q4 (Find the Vertex and Axis of Symmetry for \( f(x) = -2x^2 - 8x - 3 \))

Given: \( f(x) = -2x^2 - 8x - 3 \)

Solution:

• Factor out the -2 and complete the square: \[ f(x) = -2\left(x^2 + 4x + 4 - 4 - \frac{3}{2}\right) = -2(x + 2)^2 + 5 \]
• The vertex is \( (-2, 5) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -2 \) and \( b = -8 \): \[ x = -\frac{-8}{2(-2)} = -2 \]
• The axis of symmetry is \( x = -2 \).

Q5 (Find the Vertex and Axis of Symmetry for \( y = -x^2 + 10x - 34 \))

Given: \( y = -x^2 + 10x - 34 \)

Solution:

• Complete the square: \[ y = -(x^2 - 10x + 25 - 25 - 34) = -(x - 5)^2 - 9 \]
• The vertex is \( (5, -9) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -1 \) and \( b = 10 \): \[ x = -\frac{10}{2(-1)} = 5 \]
• The axis of symmetry is \( x = 5 \).

Q6 (Find the Vertex and Axis of Symmetry for \( y = -x^2 - 6x + 1 \))

Given: \( y = -x^2 - 6x + 1 \)

Solution:

• Complete the square: \[ y = -(x^2 + 6x + 9 - 9 + 1) = -(x + 3)^2 + 10 \]
• The vertex is \( (-3, 10) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -1 \) and \( b = -6 \): \[ x = -\frac{-6}{2(-1)} = -3 \]
• The axis of symmetry is \( x = -3 \).

Q7 (Find the Vertex and Axis of Symmetry for \( y = -4x^2 + 12x - 7 \))

Given: \( y = -4x^2 + 12x - 7 \)

Solution:

• Factor out the -4 and complete the square: \[ y = -4(x^2 - 3x + \frac{9}{4} - \frac{9}{4} - 7) = -4(x - \frac{3}{2})^2 + 2 \]
• The vertex is \( \left(\frac{3}{2}, 2\right) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -4 \) and \( b = 12 \): \[ x = -\frac{12}{2(-4)} = \frac{3}{2} \]
• The axis of symmetry is \( x = \frac{3}{2} \).

Q8: Find the Vertex and Axis of Symmetry for \( y = -9x^2 + 6x + 2 \)

Given: \( y = -9x^2 + 6x + 2 \)

Solution:

• Factor out the -9 and complete the square: \[ y = -9(x^2 - \frac{2}{3}x + \frac{1}{9} - \frac{1}{9} + 2) = -9(x - \frac{1}{3})^2 + 3 \]
• The vertex is \( \left(\frac{1}{3}, 3\right) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = -9 \) and \( b = 6 \): \[ x = -\frac{6}{2(-9)} = \frac{1}{3} \]
• The axis of symmetry is \( x = \frac{1}{3} \).

Q9: Find the Vertex and Axis of Symmetry for \( y = 4x^2 - 1 \)

Given: \( y = 4x^2 - 1 \)

Solution:

• This is already a perfect square form: \[ y = 4(x)^2 - 1 \]
• The vertex is \( (0, -1) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = 4 \) and \( b = 0 \): \[ x = 0 \]
• The axis of symmetry is \( x = 0 \).

Q10: Find the Vertex and Axis of Symmetry for \( y = x^2 - 16 \)

Given: \( y = x^2 - 16 \)

Solution:

• This is already a perfect square form: \[ y = (x)^2 - 16 \]
• The vertex is \( (0, -16) \).
• Using the formula for the axis of symmetry, \( x = -\frac{b}{2a} \), with \( a = 1 \) and \( b = 0 \): \[ x = 0 \]
• The axis of symmetry is \( x = 0 \).

Worked Examples

Q1 (Write \( y = 4x^2 + 8x - 5 \) in the form \( y = a(x + b)^2 + c \), where \( a \), \( b \), and \( c \) are integers)

Given: \( y = 4x^2 + 8x - 5 \)

Solution:

• First, factor out the coefficient of \( x^2 \) from the first two terms: \[ y = 4(x^2 + 2x) - 5 \]
• Now complete the square by adding and subtracting the square of half the coefficient of \( x \). Half of 2 is 1, and \( 1^2 = 1 \): \[ y = 4\left(x^2 + 2x + 1 - 1\right) - 5 \]
• Simplify the expression: \[ y = 4\left((x + 1)^2 - 1\right) - 5 \]
• Distribute the 4: \[ y = 4(x + 1)^2 - 4 - 5 \]
• Combine the constants: \[ y = 4(x + 1)^2 - 9 \]
• Thus, the quadratic function in the form \( y = a(x + b)^2 + c \) is: \[ y = 4(x + 1)^2 - 9 \] where \( a = 4 \), \( b = 1 \), and \( c = -9 \).

Intersection of a Quadratic Curve and a Line

Q2 (Find any points of intersection between the curve \( C \) and the line \( l \))

Given:

• Curve \( C \) has the equation \( y = x^2 - 3x + 2 \).
• Line \( l \) has the equation \( y = 3x - 7 \).

Solution:

• To find the points of intersection, set the equations for the curve and the line equal to each other: \[ x^2 - 3x + 2 = 3x - 7 \]
• Rearrange the equation to form a standard quadratic equation: \[ x^2 - 3x - 3x + 2 + 7 = 0 \implies x^2 - 6x + 9 = 0 \]
• Factor the quadratic equation: \[ (x - 3)^2 = 0 \]
• Solving for \( x \), we get: \[ x = 3 \]
• Substitute \( x = 3 \) back into the equation of the line to find the corresponding value of \( y \): \[ y = 3(3) - 7 = 9 - 7 = 2 \]
• Therefore, the point of intersection is \( (3, 2) \).

Worked Examples

Q1: Show that \( p^2 < 12q \) for the equation \( y = 3x^2 + 2px + 4q \) having no real roots

Given: \( y = 3x^2 + 2px + 4q \)

Solution:

• The general condition for a quadratic equation to have no real roots is that the discriminant must be less than zero. The discriminant \( \Delta \) of a quadratic equation \( ax^2 + bx + c = 0 \) is given by: \[ \Delta = b^2 - 4ac \]
• For the given equation \( y = 3x^2 + 2px + 4q \), the coefficients are: \[ a = 3, \quad b = 2p, \quad c = 4q \]
• Substituting these values into the discriminant formula: \[ \Delta = (2p)^2 - 4(3)(4q) = 4p^2 - 48q \]
• For the equation to have no real roots, the discriminant must be less than zero: \[ 4p^2 - 48q < 0 \]
• Simplifying the inequality: \[ 4p^2 < 48q \] Dividing both sides by 4: \[ p^2 < 12q \]
• Thus, we have shown that \( p^2 < 12q \).

Q2: Find the minimum value of the function \( f(x) = x^2 + 4x + c \), giving your answer in terms of \( c \)

Given: \( f(x) = x^2 + 4x + c \)

Solution:

• To find the minimum value of the function, we complete the square.
• First, factor the quadratic and linear terms: \[ f(x) = (x^2 + 4x) + c \]
• Complete the square by adding and subtracting the square of half the coefficient of \( x \). Half of 4 is 2, and \( 2^2 = 4 \): \[ f(x) = (x^2 + 4x + 4 - 4) + c = (x + 2)^2 - 4 + c \]
• The minimum value of \( (x + 2)^2 \) occurs when \( (x + 2)^2 = 0 \). Therefore, the minimum value of the function is: \[ f(x) = -4 + c \]
• Thus, the minimum value of the function is \( c - 4 \), and it occurs when \( x = -2 \).

Q3: Sketch the graph of \( y = 12x^2 - 5x - 72 \), labelling any points where the graph crosses the coordinate axes and the turning point

Given: \( y = 12x^2 - 5x - 72 \)

Solution:

• To sketch the graph, we need to find:
  • The x-intercepts (roots of the quadratic)
  • The y-intercept (value of \( y \) when \( x = 0 \))
  • The turning point (vertex of the parabola)

Step 1: Find the x-intercepts

• To find the x-intercepts, set \( y = 0 \) and solve the quadratic equation: \[ 12x^2 - 5x - 72 = 0 \]
• We can use the quadratic formula: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] where \( a = 12 \), \( b = -5 \), and \( c = -72 \).
• Substituting the values: \[ x = \frac{-(-5) \pm \sqrt{(-5)^2 - 4(12)(-72)}}{2(12)} = \frac{5 \pm \sqrt{25 + 3456}}{24} = \frac{5 \pm \sqrt{3481}}{24} = \frac{5 \pm 59}{24} \]
• This gives two solutions: \[ x = \frac{5 + 59}{24} = \frac{64}{24} = \frac{8}{3}, \quad x = \frac{5 - 59}{24} = \frac{-54}{24} = -\frac{9}{4} \]
• Therefore, the x-intercepts are \( x = \frac{8}{3} \) and \( x = -\frac{9}{4} \).

Step 2: Find the y-intercept

• To find the y-intercept, set \( x = 0 \): \[ y = 12(0)^2 - 5(0) - 72 = -72 \]
• The y-intercept is \( y = -72 \).

Step 3: Find the turning point

• We can find the turning point using the formula for the vertex \( x = -\frac{b}{2a} \). For the given equation, \( a = 12 \) and \( b = -5 \): \[ x = -\frac{-5}{2(12)} = \frac{5}{24} \]
• Substitute \( x = \frac{5}{24} \) into the equation to find the corresponding \( y \)-value: \[ y = 12\left(\frac{5}{24}\right)^2 - 5\left(\frac{5}{24}\right) - 72 \] Simplifying this will give the value of \( y \) at the turning point.

Worked Examples

Q1: Find the minimum value of \( x^2 - 7x + 8 \) and the corresponding value of \( x \)

Given: \( f(x) = x^2 - 7x + 8 \)

Solution:

• Complete the square to express the quadratic in the form \( a(x + b)^2 + c \): \[ f(x) = x^2 - 7x + 8 = \left(x - \frac{7}{2}\right)^2 - \frac{49}{4} + 8 \] Now simplify: \[ f(x) = \left(x - \frac{7}{2}\right)^2 - \frac{49}{4} + \frac{32}{4} = \left(x - \frac{7}{2}\right)^2 - \frac{17}{4} \]
• The minimum value occurs when \( \left(x - \frac{7}{2}\right)^2 = 0 \). This gives the minimum value of: \[ f(x) = -\frac{17}{4} \]
• The corresponding value of \( x \) is \( x = \frac{7}{2} \).
• Thus, the minimum value is \( -\frac{17}{4} \), and it occurs at \( x = \frac{7}{2} \).

Q2: Find the turning point of \( y = 7 + 5x - x^2 \) and determine if it is a maximum or minimum

Given: \( y = 7 + 5x - x^2 \)

Solution:

• Rearrange the equation to recognize the quadratic term: \[ y = -x^2 + 5x + 7 \]
• Complete the square to express the quadratic in the form \( a(x + b)^2 + c \): \[ y = -\left(x^2 - 5x + \frac{25}{4} - \frac{25}{4} + 7\right) = -\left(x - \frac{5}{2}\right)^2 + \frac{49}{4} \]
• The vertex is \( \left(\frac{5}{2}, \frac{49}{4}\right) \).
• Since the coefficient of \( x^2 \) is negative, the parabola opens downwards, and thus the turning point is a maximum point.
• Therefore, the turning point is at \( \left(\frac{5}{2}, \frac{49}{4}\right) \), and it is a maximum point.

Worked Examples

Question No:1

Solve the equation:

• \( \frac{x^{2002} + 4x^{2001}}{4x^{2000}} = 2449.25 \)

Solution:

• Start by multiplying both sides by 4 to eliminate the denominator: \[ \frac{x^{2002} + 4x^{2001}}{x^{2000}} = 9797 \]
• Factor out \( x^{2000} \) from the numerator: \[ \frac{x^{2000}(x^2 + 4x)}{x^{2000}} = 9797 \]
• Cancel \( x^{2000} \) from both sides, leading to: \[ x^2 + 4x = 9797 \]
• Rearrange the equation: \[ x^2 + 4x - 9797 = 0 \]
• Solve the quadratic equation using the quadratic formula: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] where \( a = 1 \), \( b = 4 \), and \( c = -9797 \).
• Substitute the values: \[ x = \frac{-4 \pm \sqrt{4^2 - 4(1)(-9797)}}{2(1)} = \frac{-4 \pm \sqrt{16 + 39188}}{2} = \frac{-4 \pm \sqrt{39204}}{2} \]
• Simplify: \[ x = \frac{-4 \pm 198}{2} \]
• The two possible solutions are: \[ x = \frac{-4 + 198}{2} = 97 \quad \text{or} \quad x = \frac{-4 - 198}{2} = -101 \]
• Thus, the roots of the equation are \( x = 97 \) and \( x = -101 \).

Question No: 2

Ben opened his history book and noticed that the product of the two pages in front of him was equal to 1122. What were the numbers of those pages?

Solution:

• Let the first page be \( n \). The next page is \( n + 1 \).
• The product of the pages is given by: \[ n(n + 1) = 1122 \]
• Expand the equation: \[ n^2 + n = 1122 \]
• Move all terms to the left-hand side: \[ n^2 + n - 1122 = 0 \]
• Solve the quadratic equation by factoring: \[ (n + 34)(n - 33) = 0 \]
• Set each factor to zero: \[ n + 34 = 0 \quad \text{or} \quad n - 33 = 0 \] Hence, \( n = -34 \) or \( n = 33 \).
• Since a page number cannot be negative, \( n = 33 \) is the only valid solution.
• The two pages are \( n = 33 \) and \( n + 1 = 34 \).

Worked Examples

Find the value of the following expression:

• \( \sqrt{6 + \sqrt{6 + \sqrt{6 + \cdots}}} \)

Solution:

• Let \( x \) be the value of the expression, so we can write: \[ x = \sqrt{6 + \sqrt{6 + \sqrt{6 + \cdots}}}. \]
• This simplifies to: \[ x = \sqrt{6 + x}. \]
• Square both sides to remove the square root: \[ x^2 = 6 + x. \]
• Rearrange the equation to form a quadratic equation: \[ x^2 - x - 6 = 0. \]
• Factor the quadratic equation: \[ (x - 3)(x + 2) = 0. \]
• Solve for \( x \): \[ x - 3 = 0 \quad \Rightarrow \quad x = 3, \] \[ x + 2 = 0 \quad \Rightarrow \quad x = -2. \]
• Since \( x \) must be greater than 0 (because it represents the value inside a square root), the valid solution is \( x = 3 \).
• Thus, the value of the expression is: \[ \sqrt{6 + \sqrt{6 + \sqrt{6 + \cdots}}} = 3. \]

Understanding Maximum and Minimum Values of a Quadratic Function

1. General Form

The quadratic function is represented as \( f(x) = ax^2 + bx + c \), where \( a, b, \) and \( c \) are constants and \( a \neq 0 \).

2. Shape of the Graph

The graph of a quadratic function is a parabola. The direction (upward or downward) depends on the sign of \( a \):

• If \( a > 0 \), parabola opens upwards (minimum point at vertex).

• If \( a < 0 \), parabola opens downwards (maximum point at vertex).

3. Finding the Vertex

The vertex (h, k) can be found using:

• \( h = -\frac{b}{2a} \)
• \( k = f(h) \)

4. Vertex Form of a Quadratic Function

Rewrite the function in vertex form: \( f(x) = a(x-h)^2 + k \)

5. Determining Maximum or Minimum Values

Based on the coefficient \( a \):

• Minimum Value: If \( a > 0 \), \( f(x) \) has a minimum at \( x = h \), value \( k \).
• Maximum Value: If \( a < 0 \), \( f(x) \) has a maximum at \( x = h \), value \( k \).

6. Examples

Question No: 1

Question No: 2

7. Applications

Quadratic functions are used in scenarios like projectile motion, economics, and architectural designs.