Definite Integrals:

The concept of Definite Integrals helps in finding the area under a curve over a specific interval. A definite integral has limits (or bounds) and is used to calculate the area between the curve and the x-axis, considering both positive and negative areas.

The general form of a definite integral is:

\[ \int_{a}^{b} f(x) \, dx \]

where:

• \( f(x) \) is the function being integrated,
• \( a \) and \( b \) are the lower and upper limits of the integral,
• The result is a numerical value representing the area under the curve from \( x = a \) to \( x = b \).

Key Concepts:

• Fundamental Theorem of Calculus: If \( F(x) \) is the antiderivative of \( f(x) \), then: \[ \int_{a}^{b} f(x) \, dx = F(b) - F(a) \] This means we can find the area under the curve by evaluating the antiderivative at the limits of integration.
• Interpretation: A positive result means the area is above the x-axis, and a negative result means the area is below the x-axis.

Here are some examples of definite integrals:

Example 1:

Find the value of the definite integral \( \int_{1}^{3} (2x) \, dx \).

Solution:

The function is \( f(x) = 2x \). To solve the integral:

\[ \int 2x \, dx = x^2 \]

Now evaluate from 1 to 3:

\[ \int_{1}^{3} 2x \, dx = [x^2]_{1}^{3} = 3^2 - 1^2 = 9 - 1 = 8 \]

Answer:

\[ \int_{1}^{3} 2x \, dx = 8 \]

Example 2:

Evaluate the integral \( \int_{0}^{2} (x^2 - 4) \, dx \).

Solution:

First, integrate \( f(x) = x^2 - 4 \):

\[ \int (x^2 - 4) \, dx = \frac{x^3}{3} - 4x \]

Now evaluate from 0 to 2:

\[ \int_{0}^{2} (x^2 - 4) \, dx = \left( \frac{8}{3} - 8 \right) - \left( \frac{0^3}{3} - 4 \cdot 0 \right) \]

\[ = \frac{8}{3} - \frac{24}{3} = -\frac{16}{3} \]

Answer:

\[ \int_{0}^{2} (x^2 - 4) \, dx = -\frac{16}{3} \]

Example 3:

Evaluate the definite integral \( \int_{-1}^{1} (x^3) \, dx \).

Solution:

Since \( f(x) = x^3 \) is an odd function, the area under the curve is symmetrical, but the positive and negative areas cancel each other out.

\[ \int_{-1}^{1} x^3 \, dx = 0 \]

Answer:

\[ \int_{-1}^{1} x^3 \, dx = 0 \]

Example 4:

Find the area under the curve for \( f(x) = x^2 + 3 \) from \( x = 1 \) to \( x = 2 \).

Solution:

First, integrate \( f(x) = x^2 + 3 \):

\[ \int (x^2 + 3) \, dx = \frac{x^3}{3} + 3x \]

Now evaluate from 1 to 2:

\[ \int_{1}^{2} (x^2 + 3) \, dx = \left( \frac{8}{3} + 6 \right) - \left( \frac{1}{3} + 3 \right) \]

\[ = \frac{26}{3} - \frac{10}{3} = \frac{16}{3} \]

Answer:

\[ \int_{1}^{2} (x^2 + 3) \, dx = \frac{16}{3} \]

Example 5:

Find the value of \( \int_{0}^{1} (e^x) \, dx \).

Solution:

The integral of \( e^x \) is simply \( e^x \). So we have:

\[ \int e^x \, dx = e^x \]

Now evaluate from 0 to 1:

\[ \int_{0}^{1} e^x \, dx = e^1 - e^0 = e - 1 \]

Answer:

\[ \int_{0}^{1} e^x \, dx = e - 1 \]

Solved Examples

Evaluate the definite integral:

\[ \int_{1}^{2} \frac{6x^4 - 1}{x^2} \, dx \]

Step 1: Simplify the integrand:

\[ \frac{6x^4 - 1}{x^2} = \frac{6x^4}{x^2} - \frac{1}{x^2} = 6x^2 - x^{-2} \]

The integral becomes:

\[ \int_{1}^{2} (6x^2 - x^{-2}) \, dx \]

Step 2: Integrate each term:

Integrating \(6x^2\):

\[ \int 6x^2 \, dx = 6 \cdot \frac{x^3}{3} = 2x^3 \]

Integrating \( -x^{-2} \):

\[ \int -x^{-2} \, dx = -(\frac{x^{-1}}{-1}) = \frac{1}{x} \]

Now the integral is:

\[ \int_{1}^{2} (6x^2 - x^{-2}) \, dx = \left[ 2x^3 + \frac{1}{x} \right]_{1}^{2} \]

Step 3: Evaluate the definite integral:

For \( x = 2 \):

\[ 2(2)^3 + \frac{1}{2} = 16 + \frac{1}{2} = \frac{33}{2} \]

For \( x = 1 \):

\[ 2(1)^3 + \frac{1}{1} = 2 + 1 = 3 \]

Step 4: Subtract the value at \( x = 1 \) from the value at \( x = 2 \):

\[ \frac{33}{2} - 3 = \frac{27}{2} \]

Answer:

\[ \int_{1}^{2} \frac{6x^4 - 1}{x^2} \, dx = \frac{29}{2} units \]

Question

Evaluate the definite integral:

\[ \int_{0}^{3} \sqrt{5x - 4} \, dx \]

Step 1: Use substitution:

Let \( u = 5x - 4 \), then:

\[ du = 5dx \quad \Rightarrow \quad dx = \frac{du}{5} \]

Change the limits of integration:

When \( x = 0 \), \( u = -4 \); when \( x = 3 \), \( u = 11 \).

The integral becomes:

\[ \frac{1}{5} \int_{-4}^{11} \sqrt{u} \, du \]

Step 2: Simplify the integral:

\[ \frac{1}{5} \int_{-4}^{11} u^{1/2} \, du \]

Step 3: Integrate:

Using the integral rule:

\[ \int u^{n} \, du = \frac{u^{n+1}}{n+1} \quad \text{for} \quad n \neq -1 \]

Thus:

\[ \frac{1}{5} \cdot \frac{2}{3} \left[ u^{3/2} \right]_{-4}^{11} \]

Step 4: Evaluate the definite integral:

For \( u = 11 \):

\[ u^{3/2} = 11^{3/2} = \sqrt{1331} \]

For \( u = -4 \):

\[ u^{3/2} = (-4)^{3/2} = \sqrt{-64} \quad \text{(undefined for real numbers)} \]

Answer:

The integral does not have a real solution because \( \sqrt{-64} \) is undefined for real numbers.

Question

Evaluate the definite integral:

\[ \int_{-2}^{1} \frac{12}{(5 - 3x)^3} \, dx \]

Step 1: Use substitution:

Let \( u = 5 - 3x \), then:

\[ du = -3dx \quad \Rightarrow \quad dx = \frac{du}{-3} \]

Change the limits of integration:

When \( x = -2 \), \( u = 11 \); when \( x = 1 \), \( u = 2 \).

The integral becomes:

\[ \int_{11}^{2} \frac{12}{u^3} \cdot \frac{du}{-3} \]

Step 2: Simplify the integral:

\[ \frac{12}{-3} \int_{11}^{2} u^{-3} \, du = -4 \int_{11}^{2} u^{-3} \, du \]

Step 3: Integrate:

Using the integral rule:

\[ \int u^{n} \, du = \frac{u^{n+1}}{n+1} \quad \text{for} \quad n \neq -1 \]

Thus:

\[ -4 \cdot \left[ -\frac{1}{2u^2} \right]_{11}^{2} = 2 \cdot \left[ \frac{1}{u^2} \right]_{11}^{2} \]

Step 4: Evaluate the definite integral:

For \( u = 2 \):

\[ \frac{1}{2^2} = \frac{1}{4} \]

For \( u = 11 \):

\[ \frac{1}{11^2} = \frac{1}{121} \]

Step 5: Final calculation:

\[ \frac{1}{4} - \frac{1}{121} = \frac{121 - 4}{484} = \frac{117}{484} \]

Thus:

\[ 2 \cdot \frac{117}{484} = \frac{234}{484} = \frac{117}{242} \]

Answer:

\[ \int_{-2}^{1} \frac{12}{(5 - 3x)^3} \, dx = \frac{117}{242} \]

Exercise 9E:

Evaluate:

1. a) \[ \int_{1}^{2} \left( 3x^2 - 2 + \frac{1}{x^2} \right) \, dx \]

   Solution:

   Break the integral into separate parts:

   \[ \int_{1}^{2} \left( 3x^2 - 2 + \frac{1}{x^2} \right) \, dx = \int_{1}^{2} 3x^2 \, dx - \int_{1}^{2} 2 \, dx + \int_{1}^{2} \frac{1}{x^2} \, dx \]

   Integrate each term:

   \[ \int 3x^2 \, dx = x^3, \quad \int 2 \, dx = 2x, \quad \int \frac{1}{x^2} \, dx = -\frac{1}{x} \]

   Apply limits:

   \[ \left[ x^3 \right]_{1}^{2} = 7, \quad \left[ 2x \right]_{1}^{2} = 2, \quad \left[ -\frac{1}{x} \right]_{1}^{2} = \frac{1}{2} \]

   Final result:

   \[ 7 - 2 + \frac{1}{2} = 5.5 \]

2. b) \[ \int_{-2}^{-1} \left( \frac{8 - x^2}{x^2} \right) \, dx \]

   Solution:

   Break the integrand:

   \[ \frac{8 - x^2}{x^2} = \frac{8}{x^2} - 1 \]

   Separate the integral:

   \[ \int_{-2}^{-1} \left( \frac{8}{x^2} - 1 \right) \, dx \]

   Integrate:

   \[ \int \frac{8}{x^2} \, dx = -\frac{8}{x}, \quad \int 1 \, dx = x \]

   Apply limits:

   \[ \left[ -\frac{8}{x} \right]_{-2}^{-1} = 4, \quad \left[ x \right]_{-2}^{-1} = 1 \]

   Final result:

   \[ 4 - 1 = 3 \]

3. c) \[ \int_{1}^{2} \left( x + 3 \right)\left( 7 - 2x \right) \, dx \]

   Solution:

   Expand the integrand:

   \[ (x + 3)(7 - 2x) = -2x^2 + x + 21 \]

   Integrate:

   \[ \int (-2x^2 + x + 21) \, dx = -\frac{2}{3}x^3 + \frac{1}{2}x^2 + 21x \]

   Apply limits:

   \[ -\frac{14}{3} + \frac{3}{2} + 21 = \frac{107}{6} \]

4. d) \[ \int_{0}^{1} \sqrt{x}(1 - x) \, dx \]

   Solution:

   Expand the integrand:

   \[ \sqrt{x}(1 - x) = \sqrt{x} - x^{3/2} \]

   Integrate:

   \[ \int \sqrt{x} \, dx = \frac{2}{3}x^{3/2}, \quad \int x^{3/2} \, dx = \frac{2}{5}x^{5/2} \]

   Apply limits:

   \[ \frac{2}{3} - \frac{2}{5} = \frac{4}{15} \]

5. e) \[ \int_{1}^{2} \frac{(3 - x)(8 + x)}{x^4} \, dx \]

   Solution:

   Expand the numerator:

   \[ (3 - x)(8 + x) = 24 - 5x - x^2 \]

   Integrate:

   \[ \int \frac{24}{x^4} \, dx = -\frac{8}{x^3}, \quad \int \frac{5}{x^3} \, dx = \frac{5}{2x^2}, \quad \int \frac{1}{x^2} \, dx = -\frac{1}{x} \]

   Apply limits:

   \[ 7 - \frac{15}{8} + \frac{1}{2} = \frac{45}{8} \]

6. f) \[ \int_{1}^{4} \left( 3\sqrt{x} + \frac{2}{\sqrt{x}} \right) \, dx \]

   Solution:

   Integrate:

   \[ \int 3x^{1/2} \, dx = 2x^{3/2}, \quad \int 2x^{-1/2} \, dx = 4x^{1/2} \]

   Apply limits:

   \[ 14 + 4 = 18 \]

Application Problems

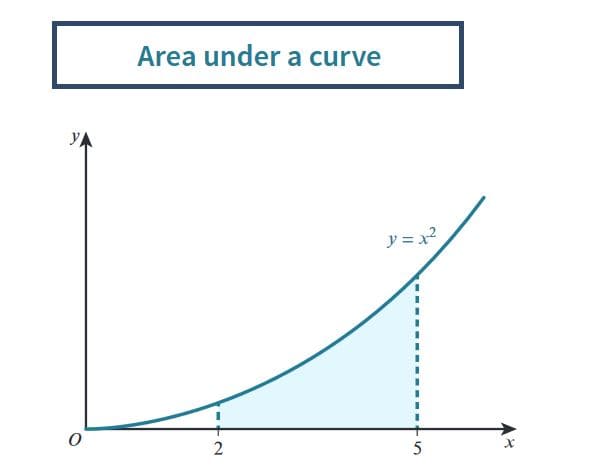
The area under a curve is found by calculating the definite integral of the function between two limits \(a\) and \(b\). The general formula is:

\[ \text{Area} = \int_{a}^{b} f(x) \, dx \]

Where \( f(x) \) is the function and \(a\) and \(b\) are the limits of integration.

Let's look at a few examples of how to compute the area under a curve:

1. Example 1: Find the area under the curve of \(y = x^2\) from \(x = 0\) to \(x = 2\).

The integral we need to evaluate is:

\[ \text{Area} = \int_{0}^{2} x^2 \, dx \]

Step-by-step solution:

1. Set up the integral:

\[ \text{Area} = \int_{0}^{2} x^2 \, dx \]

2. Integrate:

\[ \int x^2 \, dx = \frac{x^3}{3} \]

3. Apply the limits:

\[ \left[ \frac{x^3}{3} \right]_{0}^{2} = \frac{2^3}{3} - \frac{0^3}{3} = \frac{8}{3} - 0 = \frac{8}{3} \]

The area under the curve is \( \frac{8}{3} \) sqUnits.

2. Example 2: Find the area under the curve of \( y = 3x^2 + 2x \) from \(x = 1\) to \(x = 3\).

The integral we need to evaluate is:

\[ \text{Area} = \int_{1}^{3} \left( 3x^2 + 2x \right) \, dx \]

Step-by-step solution:

1. Set up the integral:

\[ \text{Area} = \int_{1}^{3} \left( 3x^2 + 2x \right) \, dx \]

2. Integrate each term:

\[ \int 3x^2 \, dx = x^3, \quad \int 2x \, dx = x^2 \]

3. Apply the limits:

\[ \left[ x^3 \right]_{1}^{3} = 3^3 - 1^3 = 27 - 1 = 26 \] \[ \left[ x^2 \right]_{1}^{3} = 3^2 - 1^2 = 9 - 1 = 8 \]

4. Final result:

\[ \text{Area} = 26 + 8 = 34 sqUnits \]

Solution:

Volume Integrals - A-Level Cambridge

Introduction to Volume Integrals

In mathematics, particularly in calculus, volume integrals are used to find the volume of solids that are defined by a function or a surface. These integrals are typically solved using the method of **integration** and **geometry**. Volume integrals are commonly encountered when determining the volume of regions in **3D space** using techniques such as the **disk method**, **washer method**, and **cylindrical shells**.

General Formulae:

The volume \( V \) of a solid of revolution about the x-axis can be calculated using the following formula:

\[ V = \pi \int_{a}^{b} \left( f(x) \right)^2 \, dx \] where \( f(x) \) is the function defining the curve and \( a \) and \( b \) are the bounds of integration along the x-axis.

The volume of a solid of revolution about the y-axis can be calculated with the formula:

\[ V = \pi \int_{c}^{d} \left( g(y) \right)^2 \, dy \] where \( g(y) \) is the function describing the curve, and \( c \) and \( d \) are the bounds along the y-axis.

Disk Method:

When the solid is generated by rotating a function \( y = f(x) \) about the x-axis (or a function \( x = g(y) \) about the y-axis), the volume is given by the formula:

\[ V = \pi \int_{a}^{b} \left( f(x) \right)^2 \, dx \] The function \( f(x) \) represents the radius of the disk at each value of \( x \).

Washer Method:

When there is a hole in the middle of the solid, we use the washer method, which involves subtracting the inner radius from the outer radius:

\[ V = \pi \int_{a}^{b} \left( \left( f(x) \right)^2 - \left( g(x) \right)^2 \right) dx \] where \( f(x) \) is the outer radius and \( g(x) \) is the inner radius of the washer at each point along the axis.

Cylindrical Shells Method:

For solids generated by rotating a function \( y = f(x) \) about the y-axis, the volume can also be found using the cylindrical shells method:

\[ V = 2\pi \int_{a}^{b} x \cdot f(x) \, dx \] where \( x \) represents the radius and \( f(x) \) represents the height of each cylindrical shell.

Example 1: Using the Disk Method

Find the volume of the solid formed by rotating the region bounded by \( y = x^2 \) and the x-axis from \( x = 0 \) to \( x = 1 \) about the x-axis.

Solution:

The formula for volume is:

\[ V = \pi \int_{a}^{b} \left( f(x) \right)^2 \, dx \] where \( f(x) = x^2 \) and the bounds are from \( x = 0 \) to \( x = 1 \). Thus, we have:

\[ V = \pi \int_{0}^{1} \left( x^2 \right)^2 \, dx = \pi \int_{0}^{1} x^4 \, dx \] Integrating \( x^4 \), we get: \[ V = \pi \left[ \frac{x^5}{5} \right]_{0}^{1} = \pi \left( \frac{1}{5} - 0 \right) = \frac{\pi}{5} \] So, the volume is \( \frac{\pi}{5} \) cubic units.

Example 2: Using the Washer Method

Find the volume of the solid formed by rotating the region bounded by \( y = x^2 \) and \( y = 1 \) about the x-axis from \( x = 0 \) to \( x = 1 \).

Solution:

Here, the volume is found using the washer method. The outer radius is \( R(x) = 1 \) and the inner radius is \( r(x) = x^2 \). The volume formula is:

\[ V = \pi \int_{0}^{1} \left( R(x)^2 - r(x)^2 \right) \, dx \] Substituting the functions \( R(x) = 1 \) and \( r(x) = x^2 \), we get: \[ V = \pi \int_{0}^{1} \left( 1^2 - \left( x^2 \right)^2 \right) \, dx = \pi \int_{0}^{1} \left( 1 - x^4 \right) \, dx \] Now, integrate: \[ V = \pi \left[ x - \frac{x^5}{5} \right]_{0}^{1} = \pi \left( 1 - \frac{1}{5} \right) = \pi \times \frac{4}{5} \] So, the volume is \( \frac{4\pi}{5} \) cubic units.

Example 3: Using the Cylindrical Shells Method

Find the volume of the solid formed by rotating the region bounded by \( y = x^2 \) and the y-axis from \( x = 0 \) to \( x = 1 \) about the y-axis.

Solution:

The formula for volume using cylindrical shells is:

\[ V = 2\pi \int_{a}^{b} x \cdot f(x) \, dx \] Here, \( f(x) = x^2 \) and the bounds are from \( x = 0 \) to \( x = 1 \). So, we have:

\[ V = 2\pi \int_{0}^{1} x \cdot x^2 \, dx = 2\pi \int_{0}^{1} x^3 \, dx \] Now, integrate \( x^3 \): \[ V = 2\pi \left[ \frac{x^4}{4} \right]_{0}^{1} = 2\pi \left( \frac{1}{4} - 0 \right) = \frac{\pi}{2} \] So, the volume is \( \frac{\pi}{2} \) cubic units.

Practice Exercises

Try solving the following volume problems:

1. Find the volume of the solid formed by rotating the region bounded by \( y = 2x \) and the x-axis from \( x = 0 \) to \( x = 3 \) about the x-axis using the disk method.
2. Find the volume of the solid formed by rotating the region bounded by \( y = x^2 \) and \( y = 4 \) about the x-axis from \( x = 0 \) to \( x = 2 \) using the washer method.
3. Find the volume of the solid formed by rotating the region bounded by \( y = \sqrt{x} \) and the x-axis from \( x = 0 \) to \( x = 4 \) about the y-axis using the cylindrical shells method.
4. Find the volume of the solid formed by rotating the region bounded by \( y = x^3 \) and the x-axis from \( x = 0 \) to \( x = 1 \) about the x-axis using the disk method.

Answer Key (Optional):

1. Volume = \( 54\pi \) cubic units
2. Volume = \( \frac{28\pi}{5} \) cubic units
3. Volume = \( 32\pi \) cubic units
4. Volume = \( \frac{\pi}{5} \) cubic units

Worksheet-Integrals

Evaluate the following integrals:

1. a) \[ \int_{0}^{1} \left( 2x^2 - 3x + 5 \right) \, dx \]
2. b) \[ \int_{1}^{2} \left( 4x^3 - 2x + 1 \right) \, dx \]
3. c) \[ \int_{0}^{3} \left( x^2 + 2x - 1 \right) \, dx \]
4. d) \[ \int_{0}^{2} \left( x^2 - 4x + 4 \right) \, dx \]
5. e) \[ \int_{1}^{3} \left( 2x^3 - 5x^2 + 4x - 1 \right) \, dx \]
6. f) \[ \int_{2}^{4} \left( 3x^2 + 2x - 7 \right) \, dx \]
7. g) \[ \int_{0}^{2} \left( x^4 - x^3 + 3x^2 - 5x \right) \, dx \]
8. h) \[ \int_{-1}^{1} \left( x^3 - x \right) \, dx \]
9. i) \[ \int_{0}^{\pi} \left( \sin(x) + \cos(x) \right) \, dx \]
10. j) \[ \int_{0}^{\pi/2} \left( \tan(x) \right) \, dx \]
11. k) \[ \int_{0}^{1} \left( \frac{1}{x} \right) \, dx \]
12. l) \[ \int_{1}^{3} \left( \frac{4}{x^2} \right) \, dx \]
13. m) \[ \int_{1}^{4} \left( \frac{1}{x^3} \right) \, dx \]
14. n) \[ \int_{2}^{5} \left( x^2 + 2x + 1 \right) \, dx \]
15. o) \[ \int_{0}^{\infty} \left( e^{-x} \right) \, dx \]
16. p) \[ \int_{-2}^{2} \left( x^2 - 4x \right) \, dx \]
17. q) \[ \int_{0}^{1} \left( x^3 + 2x^2 - x + 4 \right) \, dx \]
18. r) \[ \int_{1}^{2} \left( \frac{1}{x^2} - 3 \right) \, dx \]
19. s) \[ \int_{0}^{2} \left( 4x^2 - 6x + 2 \right) \, dx \]
20. t) \[ \int_{-3}^{0} \left( 3x^2 - 5x + 4 \right) \, dx \]

Answer Key:

1. a) \( \frac{19}{6} \)
2. b) \( 13 \)
3. c) \( 15 \)
4. d) \( \frac{8}{3} \)
5. e) \( \frac{77}{2} \)
6. f) \( 54 \)
7. g) \( \frac{32}{5} \)
8. h) \( 0 \)
9. i) \( 2 \)
10. j) \( \ln(1 + \sqrt{2}) \)
11. k) \( \infty \) (Improper Integral)
12. l) \( -\frac{1}{3} \)
13. m) \( \frac{1}{2} \)
14. n) \( 27 \)
15. o) \( 1 \)
16. p) \( \frac{16}{3} \)
17. q) \( 7 \)
18. r) \( \frac{1}{2} \)
19. s) \( \frac{8}{3} \)
20. t) \( 66 \)

Solution:

The curve is given by the equation:

\[ y = 4 - 2\sqrt{x} \]

Part (a): Find the equation of the normal \( PQ \)

Step 1: Differentiate \( y \) to find the gradient of the tangent:

\[ \frac{dy}{dx} = -\frac{2}{2\sqrt{x}} = -\frac{1}{\sqrt{x}} \]

At \( P(16, -4) \):

\[ m_{\text{tangent}} = -\frac{1}{\sqrt{16}} = -\frac{1}{4} \]

The gradient of the normal is the negative reciprocal:

\[ m_{\text{normal}} = -\frac{1}{-\frac{1}{4}} = 4 \]

The equation of the normal is:

\[ y - (-4) = 4(x - 16) \]

Simplify:

\[ y + 4 = 4x - 64 \implies y = 4x - 68 \]

Part (b): Find the coordinates of \( Q \)

At \( Q \), the normal meets the x-axis (\( y = 0 \)). Substituting \( y = 0 \):

\[ 0 = 4x - 68 \implies x = 17 \]

So, the coordinates of \( Q \) are:

\[ Q(17, 0) \]

Solution:

The curve is given by the equation:

\[ y = 2x - \frac{10}{x^2} + 8 \]

Part (a): Find \(\frac{dy}{dx}\)

Differentiate term by term:

\[ \frac{dy}{dx} = 2 - \frac{d}{dx}\left(\frac{10}{x^2}\right) \]

Using the power rule:

\[ \frac{dy}{dx} = 2 + 20x^{-3} = 2 + \frac{20}{x^3} \]

Part (b): Show that the normal passes through \( (0, -3) \)

At \( \left(-4, -\frac{5}{8}\right) \):

\[ m_{\text{tangent}} = 2 + \frac{20}{(-4)^3} = 2 + \frac{20}{-64} = 2 - \frac{5}{16} = \frac{32}{16} - \frac{5}{16} = \frac{27}{16} \]

The gradient of the normal is the negative reciprocal:

\[ m_{\text{normal}} = -\frac{1}{\frac{27}{16}} = -\frac{16}{27} \]

The equation of the normal is:

\[ y - \left(-\frac{5}{8}\right) = -\frac{16}{27}(x - (-4)) \]

Simplify:

\[ y + \frac{5}{8} = -\frac{16}{27}(x + 4) \]

Substitute \( x = 0 \):

\[ y + \frac{5}{8} = -\frac{16}{27}(4) = -\frac{64}{27} \]

Simplify further:

\[ y = -\frac{64}{27} - \frac{5}{8} \]

Converting to a common denominator:

\[ y = -3 \implies \text{Passes through } (0, -3) \]

Solution:

Differentiate the given equation w.r.t x:

\[ y = \frac{3x^5 - 7}{4x} \]

Step 1: Rewrite the equation:

\[ y = \frac{3x^5}{4x} - \frac{7}{4x} = \frac{3x^4}{4} - \frac{7}{4x} \]

Step 2: Differentiate term by term:

\[ \frac{dy}{dx} = \frac{d}{dx}\left(\frac{3x^4}{4}\right) - \frac{d}{dx}\left(\frac{7}{4x}\right) \]

\[ \frac{dy}{dx} = \frac{3}{4} \cdot 4x^3 - \frac{7}{4} \cdot \frac{-1}{x^2} \]

\[ \frac{dy}{dx} = 3x^3 + \frac{7}{4x^2} \]

Final Answer:

\[ \frac{dy}{dx} = 3x^3 + \frac{7}{4x^2} \]

Solution:

Find the Gradient of the curve, at x = 2:

\[ y = \frac{8}{4x - 5} \]

Step 1: Differentiate using the chain rule:

\[ \frac{dy}{dx} = \frac{d}{dx}\left(\frac{8}{u}\right) \cdot \frac{du}{dx}, \quad \text{where } u = 4x - 5 \]

\[ \frac{dy}{dx} = \frac{-8}{(4x - 5)^2} \cdot \frac{d}{dx}(4x - 5) \]

\[ \frac{dy}{dx} = \frac{-8}{(4x - 5)^2} \cdot 4 = \frac{-32}{(4x - 5)^2} \]

Step 2: Find the gradient at \( x = 2 \):

Substitute \( x = 2 \):

\[ \frac{dy}{dx} = \frac{-32}{(4(2) - 5)^2} = \frac{-32}{(8 - 5)^2} = \frac{-32}{9} \]

Final Answer:

The gradient at \( x = 2 \) is:

\[ \frac{-32}{9} \]

Solution:

\[ y = 3x^3 - 3x^2 + x - 7 \]

Part (a): Show that the gradient of the curve is never negative.

Step 1: Differentiate \( y \):

\[ \frac{dy}{dx} = 9x^2 - 6x + 1 \]

Step 2: Analyze the quadratic expression \( 9x^2 - 6x + 1 \):

The discriminant of a quadratic equation \( ax^2 + bx + c \) is given by:

\[ \Delta = b^2 - 4ac \]

Here, \( a = 9 \), \( b = -6 \), and \( c = 1 \):

\[ \Delta = (-6)^2 - 4(9)(1) = 36 - 36 = 0 \]

Since the discriminant is \( 0 \), the quadratic has a single root, and the parabola opens upwards (as \( a > 0 \)).

Step 3: Verify that \( \frac{dy}{dx} \geq 0 \):

The vertex of the parabola occurs at:

\[ x = -\frac{b}{2a} = -\frac{-6}{2(9)} = \frac{1}{3} \]

At the vertex, \( \frac{dy}{dx} = 0 \). For all other values of \( x \), \( \frac{dy}{dx} > 0 \) because the parabola opens upwards.

Final Answer:

The gradient of the curve is never negative.

Reference-https://mathz.org/Alevels/week12/week12.html

Differentiation Practice Worksheet

Below are 15 questions on differentiation. Solve step by step and show your working:

Part A: Basic Differentiation

Part B: Applications of Differentiation

Part C: Advanced Differentiation

Part D: Mixed Problems

End of Chapter Worsheet:

Binomial Expansion